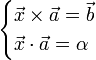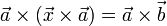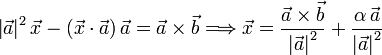Vectores libres
De Laplace
(→Producto escalar en una base ortonormal) |
(→Producto escalar) |
||
| Línea 301: | Línea 301: | ||
* Proyecciones paralelas: | * Proyecciones paralelas: | ||
<center><math>\vec{a}\cdot\vec{b}=|\,\vec{a}\,|\;\mbox{proy}_{\parallel\vec{a}}\,[\,\vec{b}\,]= |\,\vec{b}\,|\;\mbox{proy}_{\parallel\vec{b}}\,[\,\vec{a}\,]</math></center> | <center><math>\vec{a}\cdot\vec{b}=|\,\vec{a}\,|\;\mbox{proy}_{\parallel\vec{a}}\,[\,\vec{b}\,]= |\,\vec{b}\,|\;\mbox{proy}_{\parallel\vec{b}}\,[\,\vec{a}\,]</math></center> | ||
| - | |||
| - | |||
* si <math>\left|\vec{u}\right|=1</math>, entonces <math>\vec{a}\cdot\vec{u}=\mbox{proy}_{\parallel\vec{u}}\,[\,\vec{a}\,]\,</math> | * si <math>\left|\vec{u}\right|=1</math>, entonces <math>\vec{a}\cdot\vec{u}=\mbox{proy}_{\parallel\vec{u}}\,[\,\vec{a}\,]\,</math> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
====Producto escalar en una base ortonormal==== | ====Producto escalar en una base ortonormal==== | ||
| Línea 368: | Línea 349: | ||
</center> | </center> | ||
| - | + | El producto escalar de un vector <math>\vec{a}</math> por cada uno de los vectores de la base nos da la componente de dicho vector en la dirección del unitario correspondiente | |
| - | <center><math>\vec{a}=a_1\vec{u}_1+a_2\vec{u}_2+a_3 | + | <center><math>\vec{a}=a_1\vec{u}_1+a_2\vec{u}_2+a_3\vec{u}_3</math></center> |
| - | + | <center><math>a_1 = \vec{a}\cdot\vec{u}_1</math>{{qquad}}{{qquad}}<math>a_2 = \vec{a}\cdot\vec{u}_2</math>{{qquad}}{{qquad}}<math>a_3 = \vec{a}\cdot\vec{u}_3</math></center> | |
| - | + | Estas relaciones son especialmente útiles, al hacer un ''cambio de base''. Partiendo de la expresión en una determinada base ortonormal, si multiplicamos escalarmente por los unitarios de una base diferente, obtenemos las componentes en la nueva base. | |
| - | + | Reuniendo los tres resultados | |
| - | <center><math>\vec{a}\cdot\vec{u} | + | <center><math>\vec{a}=(\vec{a}\cdot\vec{u}_1)\,\vec{u}_1+ (\vec{a}\cdot\vec{u}_2)\,\vec{u}_2+(\vec{a}\cdot\vec{u}_3)\,\vec{u}_3</math></center> |
| - | + | * En particular, para las coordenadas cartesianas de un punto P | |
| - | + | <center><math>p_x = \overrightarrow{OP}\cdot\vec{\imath}</math>{{qquad}}{{qquad}}<math>p_y = \overrightarrow{OP}\cdot\vec{\jmath}</math>{{qquad}}{{qquad}}<math>p_z = \overrightarrow{OP}\cdot\vec{k}</math></center> | |
| - | + | Si tenemos dos vectores expresados en una base ortonormal (en particular, la canónica), como | |
| - | + | <center><math>\vec{a}=a_1\vec{u}_1+a_2\vec{u}_2+a_3\vec{u}_3</math>{{qquad}}{{qquad}}<math>\vec{b}=b_1\vec{u}_1+b_2\vec{u}_2+b_3\vec{u}_3</math></center> | |
| - | + | su producto escalar se compone, en principio de nueve sumandos. Sin embargo, la ortogonalidad expresada en la tabla anterior permite eliminar seis de ellos y reducir la expresión a | |
| - | + | ||
| - | + | ||
| - | * Distancia entre dos puntos | + | <center><math>\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3</math></center> |
| - | <center><math> | + | |
| - | * | + | Al poder calcular el producto escalar de dos vectores a partir de sus componentes, sin necesidad de conocer previamente los módulos y el ángulo que forman, nos permite emplear este producto para medir distancias y ángulos: |
| - | <center><math>\cos(\ | + | |
| - | :obsérvese que: | + | :*Módulo de un vector <math>\vec{a}</math>: |
| + | <center><math>a=\left|\vec{a}\right|=\sqrt{\vec{a}\cdot\vec{a}}=\sqrt{a_1^2+a_2+a_3^2}</math></center> | ||
| + | :*Distancia entre dos puntos <math>P</math> y <math>Q</math>: | ||
| + | <center><math>d(P,Q)=|\,\overrightarrow{PQ}\,|=\left|\vec{r}_Q-\vec{r}_P\right| = \sqrt{\overrightarrow{PQ}\cdot\overrightarrow{PQ}}=\sqrt{(\vec{r}_Q-\vec{r}_P)\cdot(\vec{r}_Q-\vec{r}_P)}=\sqrt{(q_x-p_x)^2+(q_y-p_y)^2+(q_z-p_z)^2}</math></center> | ||
| + | :* Ángulo formado por dos vectores <math>\vec{a}</math> y <math>\vec{b}</math>: | ||
| + | <center><math>\cos(\theta)=\frac{\vec{a}\cdot\vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right|}</math></center> | ||
| + | :* Cosenos directores de una recta <math>r</math>: | ||
| + | <center><math>\cos(\alpha_i)=\frac{\vec{a}\cdot\vec{u}_i}{\left|\vec{a}\right|}\quad(i=1,2,3) </math></center> | ||
| + | ::obsérvese que: | ||
<center><math>\cos^2(\alpha_1)+\cos^2(\alpha_2)+\cos^2(\alpha_3)=1\,</math></center> | <center><math>\cos^2(\alpha_1)+\cos^2(\alpha_2)+\cos^2(\alpha_3)=1\,</math></center> | ||
Revisión de 17:03 21 oct 2010
Contenido |
1 Tipos de magnitudes
Una magnitud física es cualquier propiedad física susceptible de ser medida. Ejemplos: el tiempo (t), la velocidad
( ), la masa (m), la temperatura (T), el campo eléctrico (
), la masa (m), la temperatura (T), el campo eléctrico (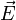 ).
).
Las magnitudes físicas se pueden clasificar en:
1.1 Magnitudes escalares
Las magnitudes escalares son aquéllas que quedan completamente determinadas mediante el conocimiento de su valor expresado mediante una cantidad (un número real) seguida de una unidad (a excepción de las adimensionales).
Ejemplos de magnitudes escalares son
- Tiempo (t)
- Masa (m)
- Temperatura (T)
- Carga eléctrica (q)
- …
1.2 Magnitudes vectoriales
Las magnitudes vectoriales son aquéllas que no quedan completamente determinadas por su valor (cantidad y unidad), sino que requieren además el conocimiento de la dirección y el sentido de su actuación y su punto de aplicación.
Entre las magnitudes vectoriales están:
- Velocidad (
 )
)
- Aceleración (
 )
)
- Fuerza (
 )
)
- Campo eléctrico (
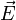 )
)
- …
Es importante tener siempre en mente la distinción entre cantidades escalares y vectoriales, ya que no pueden sumarse o igualarse cantidades de diferente tipo. Para señalar el carácter vectorial debe indicarse en la notación algún rasgo distintivo, normalmente una flecha sobre la cantidad. Así
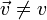
El primer símbolo,  representa la velocidad, que posee módulo, dirección y sentido (no solo nos informa de cómo de rápido se mueve una partícula sino también hacia dónde se mueve). El segundo símbolo es el módulo de la velocidad (conocido como celeridad o rapidez) que no nos informa de la dirección de movimiento.
representa la velocidad, que posee módulo, dirección y sentido (no solo nos informa de cómo de rápido se mueve una partícula sino también hacia dónde se mueve). El segundo símbolo es el módulo de la velocidad (conocido como celeridad o rapidez) que no nos informa de la dirección de movimiento.
1.3 Otros tipos de magnitudes
Además de las magnitudes escalares y vectoriales, existen otros tipos de magnitudes “de orden superior”, conocidas en general como magnitudes tensoriales.
Una magnitud escalar se puede representar por un número (con unidades), lo que equivale a una matriz 1×1. Una magnitud vectorial puede ser representadas por una vector fila o uno columna, que equivale a una matriz 1×3 o 3×1. Una magnitud tensorial requiere matrices 3×3 o incluso entes de mayores dimensiones.
Un ejemplo de magnitud tensorial son los “esfuerzos” en un sólido. Cuando se aplica una fuerza en una dirección resulta una deformación que puede ir en una dirección diferente. Por tanto necesitamos la información de la dirección y sentido de los dos, fuerza y deformación, por lo que no nos basta con una magnitud vectorial.
En este curso las magnitudes tensoriales aparecen muy raramente.
1.4 Principio de homogeneidad
Una propiedad importante de las leyes físicas es que son homogéneas. Esto quiere decir que los dos miembros de una igualdad, o cada uno de los sumandos de una suma, deben ser del mismo tipo:
- Una cantidad escalar será igual a otra cantidad escalar, por ejemplo
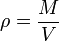
- Una cantidad vectorial será igual a otra cantidad vectorial
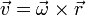
- pero nunca una cantidad escalar será igual a una vectorial. Por ejemplo, el momento de una fuerza es una cantidad cuya unidad SI es 1 N·m, y la energía cinética es una magnitud cuya unidad es 1 J = 1 N·m, pero aunque se miden en las mismas unidades, el momento de una fuerza nunca puede ser igual a la energía cinética, pues la primera es una magnitud vectorial y la segunda es una escalar
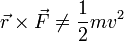
La energía cinética sí podrá ser igual al módulo del momento de la fuerza, que es una cantidad escalar
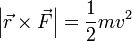
2 Vectores. Definición y clasificación
2.1 Definición
El concepto de vector es un concepto matemático con interés físico, ya que permite representar o describir las magnitudes vectoriales, así como operar con ellas.
Un vector geométrico,  , es un segmento orientado dotado de los siguientes elementos:
, es un segmento orientado dotado de los siguientes elementos:
- Módulo
- es su longitud, proporcional al valor de la magnitud física. Para indicar el módulo emplearemos tanto la notación de barras como el escribir la misma letra sin flecha:
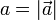
- Dirección y sentido
- es la orientación del segmento, indicada mediante una flecha y que permite definir cuál es su origen y cuál su extremo
- Punto de aplicación
- es el origen del segmento.
- Recta soporte
- es la recta a la que pertenece el segmento, definida mediante el punto de aplicación y la dirección marcada por el vector.
2.2 Tipos de vectores
Los vectores pueden clasificarse atendiendo a la cantidad de información que necesitamos para especificarlos.
2.2.1 Vectores ligados
Los vectores ligados constituyen el tipo básico. Para especificar un vector ligado necesitamos dar su módulo, dirección y sentido y punto de aplicación.
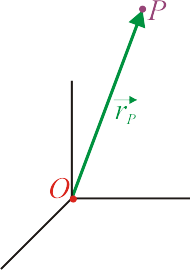
Un ejemplo inmediato de vector ligado es el vector de posición. Dado un punto O, que tomamos como origen de un sistema de referencia, y un punto P del espacio, se denomina vector de posición (o radiovector) de P al vector que tiene origen en O y extremo en P
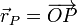
Otro ejemplo de vector ligado lo constituye el campo eléctrico, que asigna a cada punto del espacio un vector 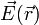 .
.
También es un vector ligado la velocidad, ya que va asociada a la posición instantánea que ocupa la partícula en movimiento.
2.2.2 Vectores deslizantes
El punto de aplicación de un vector ligado y la dirección del vector definen una recta, conocida como recta soporte.
Existen magnitudes físicas que aunque descritas en principio por vectores ligados, producen los mismos efectos si como punto de aplicación se toma cualquier otro situado en la misma recta soporte.
Un ejemplo de este tipo de vectores lo constituyen las fuerzas sobre un sólido. Es indiferente empujar un sólido por detrás o tirar de él desde delante, siempre que la recta soporte sea la misma.
Los vectores que cumplen esta propiedad se denominan vectores deslizantes (ya que pueden deslizarse libremente a lo largo de su recta soporte). Para especificar un vector deslizante, además del módulo, dirección y sentido, debe indicarse la recta soporte sobre la que se encuentra, pero no es necesario precisar un punto concreto de aplicación dentro de esta recta. O dicho de otra forma, que podemos elegir el punto de aplicación que queramos en la recta y si más adelante deseamos cambiarlo, podemos hacerlo mientras no nos salgamos de ella.
2.2.3 Vectores libres
Existen magnitudes físicas cuya descripción no requiere precisar un punto de aplicación, ni siquiera una recta soporte, pues para cualquier punto de aplicación en todo el espacio, sus consecuencias físicas son las mismas.
Un ejemplo lo tenemos en la resultante de todas las fuerzas que actúan sobre un sólido rígido.
En principio, cada magnitud física vectorial, según su naturaleza, puede ser representada por una de estas tres clases de vectores. Sin embargo, en ocasiones, es la naturaleza del problema físico concreto la que determina que una misma magnitud se describa mediante una u otra clase de vectores. Así, por ejemplo, una fuerza se comporta como un vector deslizante cuando actúa sobre un sólido rígido, y como un vector ligado cuando lo hace sobre un sólido deformable.
3 Operaciones básicas con vectores libres
3.1 Equivalencia de vectores
Dos vectores geométricos libres son equivalentes cuando poseen el mismo módulo, dirección y sentido.
3.2 Suma de vectores
Los vectores libres forman parte de un espacio vectorial, por lo que admiten la definición de las operaciones suma y producto por un escalar con una serie de propiedades algebraicas (definición algebraica de vector).
La suma de vectores libres,
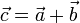
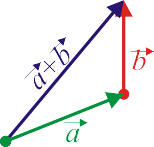
se define gráficamente de dos formas equivalentes:
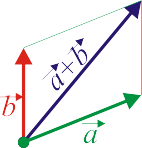
- Colocándolos con el mismo origen: la suma vectorial será la diagonal del paralelogramo que definen (regla del paralelogramo).
- Colocando uno a continuación del otro y uniendo el origen del primero con el extremo del segundo (regla del triángulo).
| 
|
| Regla del paralelogramo | Regla del triángulo |
|---|
Nótese que ambas definiciones requieren que los vectores sean libres, para que sus orígenes puedan trasladarse sin restricción.
Esta suma así definida presenta las siguientes propiedades algebraicas:
- Conmutativa
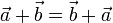
- Asociativa
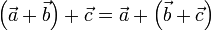
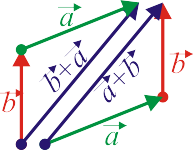
- Existencia de elemento neutro
- Existe un vector de módulo nulo,
 , tal que
, tal que
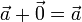
- Existencia de elemento opuesto
- Para cada vector no nulo,
 existe uno como el mismo módulo y dirección y sentido opuesto,
existe uno como el mismo módulo y dirección y sentido opuesto, 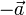 , tal que
, tal que
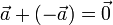
| Conmutativa | Asociativa |
|---|---|
| 
|
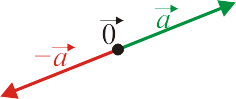
| Elemento neutro | Elemento simétrico |

| 
|
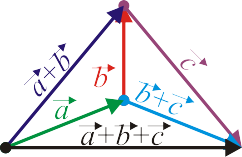
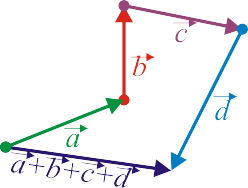
La propiedad asociativa, junto con la regla del triángulo, permite sumar n vectores a base de formar una línea quebrada disponiendo los vectores en sucesión y uniendo el origen del primero con el extremo del último.
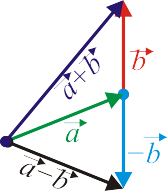
La operación suma, junto a la existencia de elemento opuesto, permite definir la resta o diferencia de vectores:
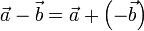
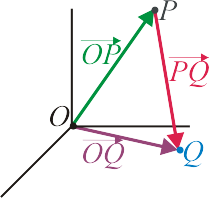
En particular, para los vectores de posición, dados dos puntos P y Q, la posición relativa de Q respecto a P es
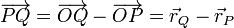
o, equivalentemente, el vector que va de O a Q es la suma vectorial del que va de O a P más el que va de P a Q:
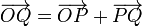
3.3 Producto por un escalar
El producto de un vector libre, , por un escalar, λ (número real), se define como un nuevo vector libre,
, por un escalar, λ (número real), se define como un nuevo vector libre, 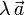 , cuyo módulo es igual al producto del escalar (en valor absoluto) por el módulo del vector original, cuya dirección es la misma que la del vector original, y cuyo sentido es el mismo o el opuesto al del vector original según el escalar sea positivo o negativo, respectivamente.
, cuyo módulo es igual al producto del escalar (en valor absoluto) por el módulo del vector original, cuya dirección es la misma que la del vector original, y cuyo sentido es el mismo o el opuesto al del vector original según el escalar sea positivo o negativo, respectivamente.
Esta operación presenta las siguientes propiedades algebraicas:
- Asociativa respecto al producto por escalar
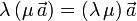
- Distributiva respecto a la suma de vectores
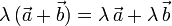
- Distributiva respecto a la suma de escalares
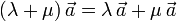
- Existencia de escalar unidad
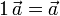
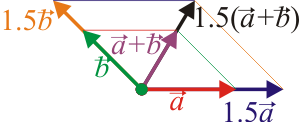
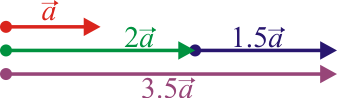
Combinando estas propiedades con las de la suma obtenemos, entre otras propiedades
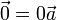
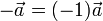
3.4 Normalización
Una vez definido el producto por un escalar, podemos obtener el vector unitario (de módulo unidad) en la dirección dada por un vector  como el vector
como el vector
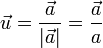
3.5 Bases
- Combinación lineal
- Uniendo las propiedades de la suma de vectores y el producto de un vector por un escalar, podemos definir una combinación lineal de n vectores mediante la expresión
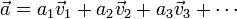
- En este caso se dice que el vector
 es linealmente dependiente de los vectores
es linealmente dependiente de los vectores 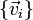 . Si no existe tal combinación lineal para obtener el vector
. Si no existe tal combinación lineal para obtener el vector  se dice que éste es linealmente independiente del conjunto.
se dice que éste es linealmente independiente del conjunto.
- Sistema generador
- Un conjunto de vectores que permiten obtener todos los demás mediante combinaciones lineales se denomina sistema generador del espacio.
- Base
- Un sistema generador cuyos vectores componentes son todos linealmente independientes entre sí (ninguno se puede poner como combinación lineal del resto) se denomina una base.
- Dimensión del espacio
- Todas las bases de un espacio vectorial poseen el mismo número de vectores. Este número es la dimensión del espacio que, en el espacio ordinario (llamado técnicamente E3) es 3.
- Desde un punto de vista geométrico, una base vectorial en el espacio ordinario E3 es cualquier terna de vectores que no sean colineales ni coplanarios.
- Base ortonormal
- Es aquella formada por tres vectores unitarios y ortogonales entre sí.
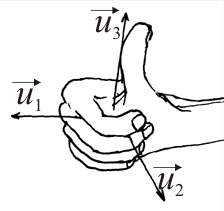
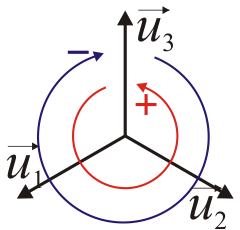
- Base ortonormal dextrógira
- Es aquella base
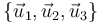 que, además de ser ortonormal tiene a sus tres vectores ordenados según la regla de la mano derecha: Si los dedos de la mano derecha van del primero al segundo, el pulgar apunta en la dirección y sentido del tercero.
que, además de ser ortonormal tiene a sus tres vectores ordenados según la regla de la mano derecha: Si los dedos de la mano derecha van del primero al segundo, el pulgar apunta en la dirección y sentido del tercero.
3.6 Componentes de un vector
Da una base B formada por la terna de vectores, 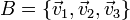 , todo vector libre,
, todo vector libre,  , se pueda expresar como una única combinación lineal de ellos, es decir:
, se pueda expresar como una única combinación lineal de ellos, es decir:
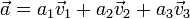
Se dice entonces que [a1,a2,a3] son las componentes del vector  en la base vectorial B.
en la base vectorial B.
Por tanto, un mismo vector tendrá una terna distinta de componentes en cada una de las infinitas bases posibles. Por ello, es importante recordar siempre qué base se está empleando para expresar dicho vector. Una forma de garantizar que esto siempre esté presente es, para todo vector, usar la expresión como combinación lineal de la base dada más arriba.
De la propiedad de que la expresión de un vector en una base sea única se deduce que dos vectores son iguales si y solo sí son iguales dos a dos sus componentes en la misma base.
3.7 Coordenadas de un punto
Los puntos del espacio pueden etiquetarse mediante letras, O, P, Q,… Sin embargo, para operar con ellos, es conveniente emplear coordenadas, que no son más que etiquetas numéricas que identifican cada punto de forma unívoca.
Existen muchos sistemas de coordenadas posibles. Las más sencillas son las coordenadas cartesianas
Dado un punto del espacio, O, que tomamos como origen de coordenadas, tomamos tres planos que pasan por dicho punto y que sean ortogonales entre sí, que denominaremos XY, XZ e YZ. Definimos entonces las coordenadas cartesianas de cualquier otro punto como las distancias (con signo), x, y, z a estos planos coordenados (x la distancia al YZ, y al XZ, y z al XY).
Los planos se cortan en tres rectas, también ortogonales entre sí, que denominamos ejes de coordenadas OX, OY y OZ (o simplemente X, Y y Z). Los vectores unitarios tangentes a estos ejes forman una base ortonormal  , de forma que la posición de cualquier punto P puede expresarse mediante su vector de posición, que es aquél que tiene como origen el de coordenadas y como extremo el punto P (es, por tanto, un vector ligado)
, de forma que la posición de cualquier punto P puede expresarse mediante su vector de posición, que es aquél que tiene como origen el de coordenadas y como extremo el punto P (es, por tanto, un vector ligado)
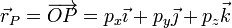
La posición del origen de coordenadas y la orientación de los ejes son arbitrarias. Por ello no hay que presuponer que, por ejemplo, “el eje Z es vertical”. Nadie se encuentra un eje Z por la calle. El eje Z será el que nosotros queramos que sea y si nos interesa que forme un ángulo de 37° respecto al suelo, pues así lo podemos tomar.
En forma abreviada, la posición del punto P se puede escribir en la forma P(px,py,pz)
La posición relativa del punto Q respecto al punto P la da el vector que tiene por origen P y por extremo Q. Es inmediato obtener las componentes de este vector en la base cartesiana, conocidas las coordenadas cartesianas del origen y del extremo. Basta restarle las primeras a las segundas. Si P(px,py,pz) y Q(qx,qy,qz), el vector 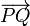 es:
es:
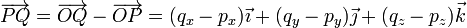
4 Productos entre vectores
4.1 Producto escalar
4.1.1 Definición
Dados dos vectores,  y
y  , que forman un ángulo θ (
, que forman un ángulo θ (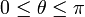 ), se denomina producto escalar,
), se denomina producto escalar, 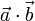 , al escalar (número real) que resulta de multiplicar los módulos de ambos vectores por el coseno del ángulo que forman:
, al escalar (número real) que resulta de multiplicar los módulos de ambos vectores por el coseno del ángulo que forman:
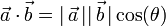
En la notación de producto escalar es importante el incluir el punto entre los vectores. También es crucial el recordar que toma dos vectores y produce como resultado una magnitud escalar.
A pesar de la similitud en el nombre, es importante no confundir el producto escalar de dos vectores con el producto de un vector por un escalar (que toma un vector y un escalar y da como resultado un vector).
4.1.2 Propiedades
El producto escalar presenta las siguientes propiedades algebraicas:
- Asociativa respecto al producto por un escalar
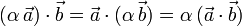
- Conmutativa
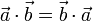
- Distributiva respecto a la suma
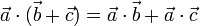
- Cancelativa
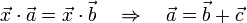 siendo
siendo  y por tanto
y por tanto 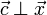
El producto escalar NO cumple la propiedad asociativa. Para empezar, porque el producto escalar de tres vectores ni siquiera está definido. En segundo lugar, porque se tiene que
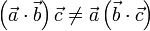
El primer miembro es el producto del vector 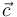 por un número, resultando un vector en la dirección de
por un número, resultando un vector en la dirección de 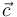 ; el segundo miembro apunta en la dirección de
; el segundo miembro apunta en la dirección de  . por tanto, no pueden ser iguales.
. por tanto, no pueden ser iguales.
El producto escalar presenta las siguientes propiedades geométricas:
- Condición de ortogonalidad: si
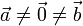 entonces
entonces
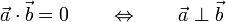
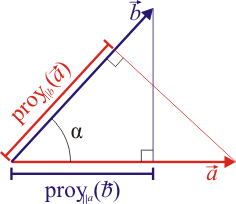
- Proyecciones paralelas:
![\vec{a}\cdot\vec{b}=|\,\vec{a}\,|\;\mbox{proy}_{\parallel\vec{a}}\,[\,\vec{b}\,]= |\,\vec{b}\,|\;\mbox{proy}_{\parallel\vec{b}}\,[\,\vec{a}\,]](/wiki/images/math/2/f/e/2fee7fc2f1e9d6fb197964401807fa3f.png)
- si
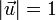 , entonces
, entonces ![\vec{a}\cdot\vec{u}=\mbox{proy}_{\parallel\vec{u}}\,[\,\vec{a}\,]\,](/wiki/images/math/6/d/0/6d00c65b125450daeb0a2763949361be.png)
4.1.3 Producto escalar en una base ortonormal
Una base 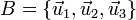 es ortonormal cuando sus vectores son ortogonales entre sí, y unitarios.
es ortonormal cuando sus vectores son ortogonales entre sí, y unitarios.
La condición de ortogonalidad se expresará
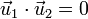
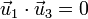
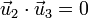
y la de que los vectores sean unitarios
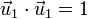
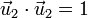
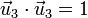
Estos resultados se pueden resumir como
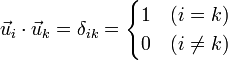
donde a δik se la denomina delta de Kronecker
Para el caso particular de la base canónica  podemos construir la siguiente tabla de multiplicar
podemos construir la siguiente tabla de multiplicar

| 
| 
| 
|
|---|---|---|---|

| 1 | 0 | 0 |

| 0 | 1 | 0 |

| 0 | 0 | 1 |
El producto escalar de un vector  por cada uno de los vectores de la base nos da la componente de dicho vector en la dirección del unitario correspondiente
por cada uno de los vectores de la base nos da la componente de dicho vector en la dirección del unitario correspondiente
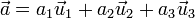
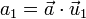
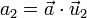
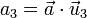
Estas relaciones son especialmente útiles, al hacer un cambio de base. Partiendo de la expresión en una determinada base ortonormal, si multiplicamos escalarmente por los unitarios de una base diferente, obtenemos las componentes en la nueva base.
Reuniendo los tres resultados
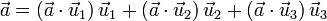
- En particular, para las coordenadas cartesianas de un punto P
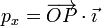
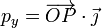
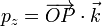
Si tenemos dos vectores expresados en una base ortonormal (en particular, la canónica), como
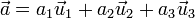
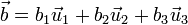
su producto escalar se compone, en principio de nueve sumandos. Sin embargo, la ortogonalidad expresada en la tabla anterior permite eliminar seis de ellos y reducir la expresión a
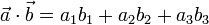
Al poder calcular el producto escalar de dos vectores a partir de sus componentes, sin necesidad de conocer previamente los módulos y el ángulo que forman, nos permite emplear este producto para medir distancias y ángulos:
- Módulo de un vector
 :
:
- Módulo de un vector
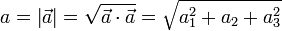
- Distancia entre dos puntos P y Q:
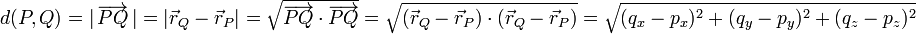
- Ángulo formado por dos vectores
 y
y  :
:
- Ángulo formado por dos vectores
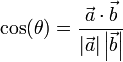
- Cosenos directores de una recta r:
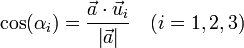
- obsérvese que:
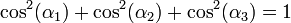
4.1.4 Ecuación vectorial del plano
Finalmente, como aplicación geométrica del producto escalar, se puede deducir la ecuación vectorial normal del plano, Π, que pasa por el punto P0(x0,y0,z0) con vector de posición
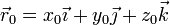
y que es normal al vector
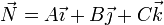
Si P(x,y,z) es un punto genérico del plano con vector de posición
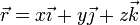
entonces
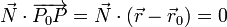
Esta es la ecuación vectorial del plano. Desarrollando obtenemos su ecuación implícita
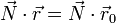

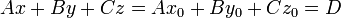
4.2 Producto vectorial
4.2.1 Definición
Dados dos vectores,  y
y  , que forman un ángulo θ (
, que forman un ángulo θ (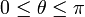 ), se denomina producto vectorial,
), se denomina producto vectorial, 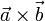 , a un nuevo vector tal que
, a un nuevo vector tal que
- Módulo
- Es igual al producto de los módulos de los dos vectores por el seno del ángulo que forman. Equivalentemente, es el área del paralelogramo que definen ambos vectores.
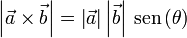
- Dirección
- la perpendicular al plano definido por los vectores
 y
y  .
.
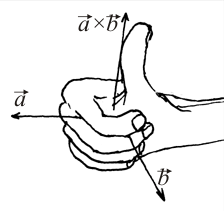
- Sentido
- el dado por la regla de la mano derecha: si colocamos nuestra mano derecha de forma que los dedos sigan el sentido de giro desde el primer vector,
 , hacia el segundo vector,
, hacia el segundo vector,  , por el camino más corto, entonces el pulgar extendido apunta en el sentido de
, por el camino más corto, entonces el pulgar extendido apunta en el sentido de 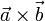 .
.
4.2.2 Propiedades
El producto vectorial presenta las siguientes propiedades algebraicas:
- No es asociativo
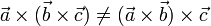
- Anticonmutativa
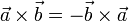
- Asociativa respecto al producto por un escalar
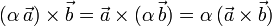
- Distributiva respecto a la suma
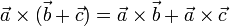
- Cancelativa
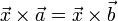

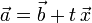 siendo t un parámetro real
siendo t un parámetro realEl producto vectorial presenta las siguientes propiedades geométricas:
- Condición de paralelismo: Si
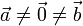

- Proyecciones ortogonales
![\left|\vec{a}\times\vec{b}\right|=\left|\vec{a}\right|\mbox{proy}_{\perp\vec{a}}\,[\,\vec{b}\,]=
\left|\vec{b}\right|\mbox{proy}_{\perp\vec{b}}\,[\,\vec{a}\,]](/wiki/images/math/a/7/0/a7059e7cc08e03bbe5ac6482cf20c751.png)
- Si
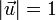 entonces:
entonces:
![\left|\vec{a}\times\vec{u}\right|=\mbox{proy}_{\perp\vec{u}}\,[\,\vec{a}\,]](/wiki/images/math/1/6/4/164dd723ce541e940b28d0c483e4e0b5.png)
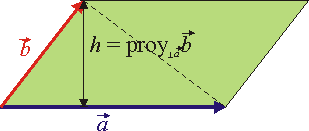
- El módulo del producto vectorial de dos vectores,
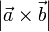 , es igual al área del paralelogramo que tiene como lados a ambos vectores, o -lo que es lo mismo- es igual al doble del área del triángulo que tiene a ambos vectores como dos de sus lados.
, es igual al área del paralelogramo que tiene como lados a ambos vectores, o -lo que es lo mismo- es igual al doble del área del triángulo que tiene a ambos vectores como dos de sus lados.
4.2.3 Producto en una base ortonormal
En una base ortonormal, el producto del primer vector de la base, 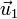 , por el segundo de ella,
, por el segundo de ella, 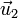 , produce un vector en la dirección ortogonal a ellos. Esta dirección es la del tercer vector
, produce un vector en la dirección ortogonal a ellos. Esta dirección es la del tercer vector 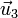 , pero, en principio, su sentido puede ser el de este tercer vector o el opuesto. En las aplicaciones en física se consideran exclusivamente bases ortonormales dextrógiras, en las que se verifica la regla de la mano derecha:
, pero, en principio, su sentido puede ser el de este tercer vector o el opuesto. En las aplicaciones en física se consideran exclusivamente bases ortonormales dextrógiras, en las que se verifica la regla de la mano derecha:
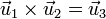
Más en general se tienen los productos:
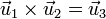
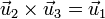
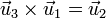
Si invertimos el orden de los vectores, cambia el signo de los resultados
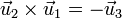
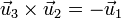
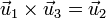
Vemos que es importante tener en cuenta el orden de los vectores de una base, que no se pueden dar de cualquier manera, si se quiere mantener su carácter dextrógiro.
Particularizando para la base canónica  obtenemos la siguiente tabla de multiplicar
obtenemos la siguiente tabla de multiplicar
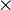
| 
| 
| 
|
|---|---|---|---|

| 
| 
| 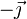
|

| 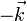
| 
| 
|

| 
| 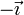
| 
|
- Producto vectorial de dos vectores arbitrarios,
 y
y  (se deduce del punto anterior y de las propiedades algebraicas):
(se deduce del punto anterior y de las propiedades algebraicas):
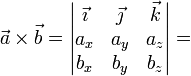
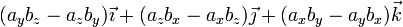
4.2.4 Ecuación vectorial de la recta
Finalmente, como aplicación geométrica del producto vectorial, se puede deducir la ecuación vectorial de la recta, r, que pasa por el punto P0(x0,y0,z0) con vector de posición
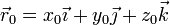
y que va en la dirección del vector
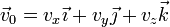
Si P(x,y,z) es un punto genérico de la recta r, con vector de posición
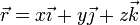
entonces
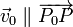

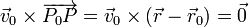
Esta es la ecuación vectorial de la recta.
Aplicando la propiedad cancelativa del producto vectorial obtenemos la ecuación paramétrica de la recta
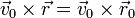

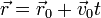
siendo t un parámetro real. Desarrollando en las componentes cartesianas obtenemos el sistema de ecuaciones paramétricas
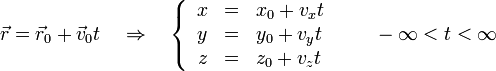
Eliminando el parámetro t llegamos a las ecuaciones contínuas
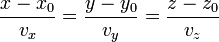
4.3 Producto mixto
4.3.1 Definición
Se define el producto mixto de tres vectores como la cantidad escalar
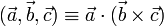
4.3.2 Propiedades
El producto mixto presenta las siguientes propiedades algebraicas:
- Permutabilidad cíclica:
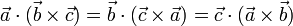
- Antipermutabilidad acíclica:
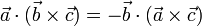
- Intercambio de signos
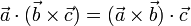
- Nótese que no basta con cambiar los paréntesis de sitio, también hay que intercambiar los signos de producto escalar y producto vectorial.
El producto mixto presenta las siguientes propiedades geométricas:
- El valor absoluto del producto mixto de tres vectores,
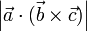 , es igual al volumen del paralelepípedo que tiene como aristas a esos tres vectores:
, es igual al volumen del paralelepípedo que tiene como aristas a esos tres vectores:
![\left|\vec{a}\cdot(\vec{b}\times\vec{c})\right|=\left|\vec{b}\times\vec{c}\right|\; \mbox{proy}_{\parallel(\vec{b}\times\vec{c})}\,[\,\vec{a}\,]=\mbox{Volumen}](/wiki/images/math/5/e/6/5e648d852ec84de53c1b83ac99ed5149.png)
- Condición de coplanariedad, para
 ,
,  y
y 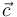 no nulos:
no nulos:

Aplicación:
- Tres vectores,
 ,
,  y
y 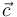 , constituyen una base vectorial del espacio ordinario E3 si, y sólo si,
, constituyen una base vectorial del espacio ordinario E3 si, y sólo si,
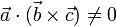
4.3.3 Producto en una base ortonormal
El producto mixto de tres vectores expresados en una base ortonormal dextrógira, en particular la canónica, se expresa:
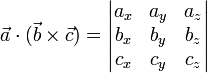
Aplicaciones:
- Producto mixto de los vectores de una base ortonormal dextrógira,
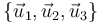 :
:
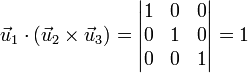
En particular
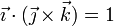
- Dependencia lineal. Si para tres vectores se anula su producto mixto
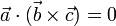
- entonces existen escalares λ, μ y ν no nulos tales que
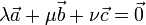
- Despejando, alguno de los vectores puede ponerse combinación lineal de los otros dos.
- Ecuación del plano, Π, que pasa por tres puntos no alineados, P1(x1,y1,z1), P2(x2,y2,z2) y P3(x3,y3,z3). Todo punto P(x,y,z) que pertenezca al plano Π debe satisfacer la ecuación:
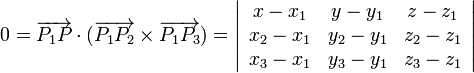
4.4 Doble producto vectorial
El producto vectorial de dos vectores se puede multiplicar por un tercero, resultando un nuevo vector
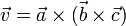
El resultado de este producto es un vector perpendicular a 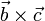 y por tanto contenido en el plano definido por
y por tanto contenido en el plano definido por  y
y 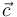 , esto es, debe ser de la forma
, esto es, debe ser de la forma
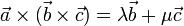
Puede demostrarse que
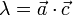
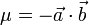
y el doble producto vectorial es igual a
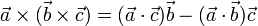
Este producto NO verifica la propiedad asociativa.
Empleando la propiedad anticonmutativa del producto vectorial se llega al resultado
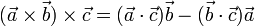
que no coincide con el anterior (éste está contenido en el plano definido por  y
y  .
.
En su lugar, el doble producto vectorial satisface la identidad de Jacobi
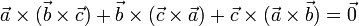
Aplicaciones:
- Desarrollo del producto escalar de dos productos vectoriales:
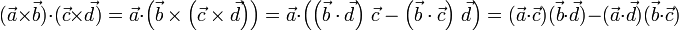
- Descomposición de un vector en componente paralela y componente ortogonal a otro vector: Dado un vector
 no nulo y un vector
no nulo y un vector  ,
,  se puede escribir como suma de un vector paralelo a
se puede escribir como suma de un vector paralelo a  y uno ortogonal a él se pueden hallar como
y uno ortogonal a él se pueden hallar como
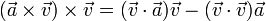
Despejando de aquí
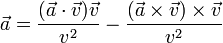
El primer término es paralelo a  , mientras que el segundo es ortogonal, por lo que la descomposición de
, mientras que el segundo es ortogonal, por lo que la descomposición de  es
es
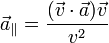
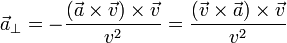
- Resolver, para la incógnita
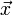 , el sistema de ecuaciones vectoriales
, el sistema de ecuaciones vectoriales