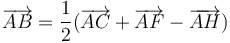No Boletín - Aplicación de la regla del paralelogramo (Ex.Oct/14)
De Laplace
1 Enunciado
Las ternas de vectores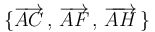 
y 
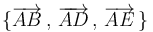están asociadas al paralelepípedo de la figura. Corresponden, respectivamente, a las diagonales de vértice común de tres caras contiguas y a las tres aristas que concurren en ese mismo vértice. Observe que la regla del
paralelogramo para la suma vectorial permite establecer relaciones entre los vectores de una y otra terna.
¿Cuál de las siguientes relaciones de equivalencia es correcta?
(NOTA: sólo una de las cuatro opciones es correcta).
- (1)
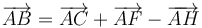
- (2)
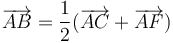
- (3)
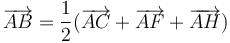
- (4)
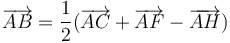
2 Solución
Las caras de un paralelepípedo son paralelogramos. Así que, observando la figura y conforme a la regla del paralelogramo para la suma vectorial, se pueden establecer las siguientes relaciones de equivalencia:
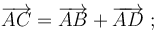
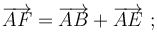
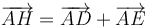
Entonces, si a la suma de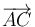 
y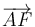 
le restamos 
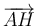, queda:
y, finalmente, despejando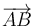 
, comprobamos que la relación de equivalencia correcta es la (4):
