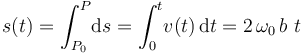Partícula en movimiento con trayectoria y ley horaria conocidas, Enero 2018 (F1 GIA)
De Laplace
Contenido |
1 Enunciado
Una partícula P se mueve respecto de un sistema de referencia cartesiano OXYZ, recorriendo la curva Γ descrita por la ecuación paramétrica:
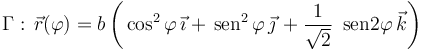
El movimiento de la partícula tiene lugar en el intervalo 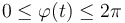 , según la ley horaria
, según la ley horaria 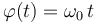 . Los parámetros b y ω0 tienen valores constantes conocidos.
. Los parámetros b y ω0 tienen valores constantes conocidos.
Obtenga las expresiones de las componentes intrínsecas y cartesianas de la velocidad y la aceleración, en función del tiempo. Obtenga también la ley horaria 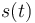 para el parámetro arco.
para el parámetro arco.
2 Solución
En el enunciado se nos proporciona una expresión vectorial paramétrica de la trayectoria Γ seguida por la partícula P, en términos de un parámetro geométrico  , que se corresponde con un determinado ángulo. Obsérvese que no se indica como se define dicho ángulo, sin embargo, no es necesario conocer esta información para resolver el ejercicio, pues es suficiente con saber cuál es la ley horaria
, que se corresponde con un determinado ángulo. Obsérvese que no se indica como se define dicho ángulo, sin embargo, no es necesario conocer esta información para resolver el ejercicio, pues es suficiente con saber cuál es la ley horaria  que describe cómo va recorriendo la partícula la trayectoria durante su movimiento. Como sabemos, la composición de una expresión paramétrica de la trayectoria con la ley horaria para dicho parámetro, proporciona la expresión vectorial que denominamos ecuaciones horarias y que consiste en el vector posición de la partícula medido con respecto de un punto fijo O y expresado como una función vectorial del tiempo:
que describe cómo va recorriendo la partícula la trayectoria durante su movimiento. Como sabemos, la composición de una expresión paramétrica de la trayectoria con la ley horaria para dicho parámetro, proporciona la expresión vectorial que denominamos ecuaciones horarias y que consiste en el vector posición de la partícula medido con respecto de un punto fijo O y expresado como una función vectorial del tiempo:
![\left.\begin{array}{r}\displaystyle P\in \Gamma: \!\ \vec{r}(\varphi)= b\!\ \bigg(\cos^2 \varphi
\!\ \vec{\imath}+\,\mathrm{sen}^2\,
\varphi\!\ \vec{\jmath}\!\ +\frac{1}{\sqrt{2}}\ \,\mathrm{sen} 2\varphi\!\ \vec{k}\bigg) \\ \\ \displaystyle \varphi (t)=\omega_0\!\ t\mathrm{;}\,\,\;\;\mathrm{con}\;\;\,\;\; 0\leq t \leq \frac{2\pi}{\omega_0}\end{array}\right\}\,\Longrightarrow\; \overrightarrow{OP}=\vec{r}\ [\varphi(t)]=x(t)\!\ \vec{\imath}+\!\ y(t)\!\ \vec{\jmath}+\!\ z(t)\!\ \vec{k}\mathrm{;}\;\;\,\mathrm{con}\;\; \left\{\begin{array}{l} x(t)=b\cos^2 (\omega_0\!\ t)\\ \\ y(t)=b\,\mathrm{sen}^2\, (\omega_0\!\ t)\\ \\ \displaystyle z(t)=\frac{b}{\sqrt{2}}\ \,\mathrm{sen}\, (2\!\ \omega_0\!\ t)\end{array}\right.](/wiki/images/math/a/a/1/aa1cb14a31c981c110e372cf3e63e6e7.png)
Es decir, las ecuaciones horarias que describen el movimiento de una partícula pueden considerarse como un caso particular de expresión paramétrica de la trayectoria, pero utilizando como parámetro la magnitud física tiempo, en lugar de una variable geométrica.
2.1 Expresiones de la velocidad instantánea
La velocidad instantánea de una partícula se define como la variación que por unidad de tiempo experimenta el radio vector que indica la posición de la partícula respecto del origen O del sistema de referencia. La expresión analítica de dicha magnitud vectorial se obtiene derivando con respecto al tiempo las ecuaciones horarias:
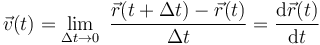
- Coordenadas cartesianas
Como las ecuaciones horarias están expresadas analíticamente en términos de la base cartesiana  asociada al sistema de referencia OXYZ, al derivar aquéllas con respecto al tiempo obtendremos la expresión analítica de la velocidad en dicha base vectorial. Nótese que la base cartesiana está ligada a un sistema de referencia fijo OXYZ por lo que sus vectores, además de tener módulo constante (igual a la unidad), tienen también dirección y sentido permanentes. Es decir, no son función del tiempo ni del parámetro geométrico
asociada al sistema de referencia OXYZ, al derivar aquéllas con respecto al tiempo obtendremos la expresión analítica de la velocidad en dicha base vectorial. Nótese que la base cartesiana está ligada a un sistema de referencia fijo OXYZ por lo que sus vectores, además de tener módulo constante (igual a la unidad), tienen también dirección y sentido permanentes. Es decir, no son función del tiempo ni del parámetro geométrico  , por lo que sus derivadas con respecto a cualquiera de estos parámetros son nulas. Por otra parte, como las ecuaciones horarias están expresadas en términos de la ley
, por lo que sus derivadas con respecto a cualquiera de estos parámetros son nulas. Por otra parte, como las ecuaciones horarias están expresadas en términos de la ley  , a efectos de cálculo puede resultar más cómodo realizar la derivación mediante la aplicación de la regla de la cadena:
, a efectos de cálculo puede resultar más cómodo realizar la derivación mediante la aplicación de la regla de la cadena:
![\vec{v}(t)=\frac{\mathrm{d}\vec{r}(t)}{\mathrm{d}t}=\frac{\mathrm{d}\vec{r}[\varphi(t)]}{\mathrm{d}t}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}\varphi}\ \frac{\mathrm{d}\varphi}{\mathrm{d}t}\mathrm{;}\,\;\;\,\mathrm{siendo}\,\;\;\left\{\begin{array}{l}\displaystyle \frac{\mathrm{d}\vec{r}}{\mathrm{d}\varphi}= b\!\ \bigg(-\,\mathrm{sen} 2\varphi
\ \vec{\imath}+\,\mathrm{sen}\,
2\varphi\ \vec{\jmath}\!\ +\frac{2}{\sqrt{2}}\ \cos 2\varphi\ \vec{k}\bigg) \\ \\ \displaystyle \frac{\mathrm{d}\varphi}{\mathrm{d}t}=\omega_0\mathrm{,}\,\;\;\mathrm{cte.}\end{array}\right.](/wiki/images/math/2/d/c/2dc6a58854238297f07659b62e813fce.png)
Se obtiene así la expresión analítica de la velocidad en la base cartesiana, como una función del tiempo y de la posición de la partícula, dada por el valor de la variable geométrica  en cada instante de tiempo:
en cada instante de tiempo:
![\vec{v}[\varphi(t)]=\omega_0\!\ b \!\ \bigg[-\mathrm{sen} 2\varphi(t)
\ \vec{\imath}+\,\mathrm{sen}\,
2\varphi(t)\ \vec{\jmath}\!\ +\sqrt{2}\!\ \cos 2\varphi(t)\ \vec{k}\bigg]=v_x(t)\ \vec{\imath}\!\ + \!\ v_y(t)\ \vec{\jmath}\!\ + \ v_z(t)\!\ \vec{k}\mathrm{;}\;\;\;\,\mathrm{siendo}\;\;\; \left\{\begin{array}{l} v_x(t)=\dot{x}(t)=-\omega_0\!\ b\,\mathrm{sen}\, (2\!\ \omega_0\!\ t)\\ \\ v_y(t)=\dot{y}(t)=\omega_0\!\ b\,\mathrm{sen}\, (2\!\ \omega_0\!\ t)\\ \\ \displaystyle v_z(t)=\dot{z}(t)=\omega_0\!\ b\ \sqrt{2}\ \,\mathrm{cos}\, (2\!\ \omega_0\!\ t)\end{array}\right.](/wiki/images/math/2/1/7/21702d7c7ee91340aea853d35d2cfb1b.png)
- Componentes intrínsecas
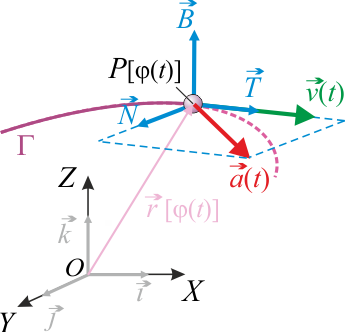
Sea una partícula o punto material 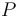 que se mueve en el espacio siguiendo una determinada trayectoria
que se mueve en el espacio siguiendo una determinada trayectoria 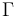 . En cada punto de dicha trayectoria se puede definir una base local ortonormal,
. En cada punto de dicha trayectoria se puede definir una base local ortonormal,
![\overrightarrow{OP}=\vec{r}(t)\mathrm{,}\;\;\,\mathrm{tal}\;\;\,\mathrm{que}\,\;\; \Gamma:\ \vec{r}\ [\lambda(t)]\;\;\longrightarrow\;\; \bigg\{\vec{T}(P)\mathrm{;}\ \vec{N}(P)\mathrm{;}\ \vec{B}(P)\bigg\}_{P\in\Gamma}](/wiki/images/math/8/9/8/898f3db913e6de92ac5c7ea91933dd2f.png)
que son, respectivamente, los vectores tangente, normal y binormal. La dirección y sentido de estos vectores depende de las propiedades geométricas de la curva 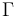 , por lo que a esta base del espacio vectorial real, euclídeo y tridimensional, es denominada como triedro intrínseco. En consecuencia, las componentes de una magnitud física de carácter vectorial, expresada analíticamente en dicha base local, son las componentes intrínsecas de la magnitud. Como se sabe, esta base intrínseca a la trayectoria, también llamada triedro de Frenet, es especialmente interesante para describir las magnitudes cinemáticas que describe el movimiento de una partícula o punto material.
, por lo que a esta base del espacio vectorial real, euclídeo y tridimensional, es denominada como triedro intrínseco. En consecuencia, las componentes de una magnitud física de carácter vectorial, expresada analíticamente en dicha base local, son las componentes intrínsecas de la magnitud. Como se sabe, esta base intrínseca a la trayectoria, también llamada triedro de Frenet, es especialmente interesante para describir las magnitudes cinemáticas que describe el movimiento de una partícula o punto material.
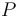 de la trayectoria Γ de una partícula es un vector unitario que tiene la dirección de la recta tangente a la curva Γ en el punto
de la trayectoria Γ de una partícula es un vector unitario que tiene la dirección de la recta tangente a la curva Γ en el punto 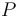 , y su sentido es el del movimiento de la partícula en dicho punto. En consecuencia, este vector debe ser colineal con el vector desplazamiento
, y su sentido es el del movimiento de la partícula en dicho punto. En consecuencia, este vector debe ser colineal con el vector desplazamiento 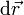 l entre la posición de la partícula en un instante t y la que ocupará en el instante inmediatamente posterior t + dt en que la distancia dsentre dichas posiciones coindice con el módulo del vector desplazamiento. En consecuencia, el vector tangente en cada punto de la trayectoria debe ser colineal con el vector velocidad instantánea, y como además debe ser un vector unitario...
l entre la posición de la partícula en un instante t y la que ocupará en el instante inmediatamente posterior t + dt en que la distancia dsentre dichas posiciones coindice con el módulo del vector desplazamiento. En consecuencia, el vector tangente en cada punto de la trayectoria debe ser colineal con el vector velocidad instantánea, y como además debe ser un vector unitario...

... se tendrá que, en todo instante y para toda posición, la velocidad instantánea de una partícula en movimiento tiene una única componente intrínseca: la componente en la dirección del vector tangente a la trayectoria en el punto 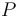 ocupado por la partícula en dicho instante. Además, dicha componente, habitualmente llamada celeridad, es igual al módulo del vector velocidad instantánea. En el caso analizado, cuando en un instante
ocupado por la partícula en dicho instante. Además, dicha componente, habitualmente llamada celeridad, es igual al módulo del vector velocidad instantánea. En el caso analizado, cuando en un instante  la partícula ocupa la posición dada
por el valor
la partícula ocupa la posición dada
por el valor  , la expresión de la velocidad instantánea de la partícula en el triedo intrínseco es:
, la expresión de la velocidad instantánea de la partícula en el triedo intrínseco es:
![\overrightarrow{OP}=\vec{r}\ [\varphi(t)]\;\Longrightarrow](/wiki/images/math/4/e/2/4e2aaa3b08400b5f1c2b833cc14a46eb.png)
![\vec{v}(t)=v(t)\ \vec{T}(P)\ \mathrm{,}\quad \mathrm{con}\;\left\{\begin{array}{l}\displaystyle v(t)=|\vec{v}(t)|=\omega_0\!\ b\!\ \sqrt{2\,\mathrm{sen}^2\,[2\!\ \varphi(t)]\ + \ 2\cos^2[2\!\ \varphi(t)]}=\sqrt{2}\ \omega_0\!\ b\\ \\
\displaystyle \vec{T}[P(\varphi)]=\frac{\vec{v}(t)}{|\vec{v}(t)|}=\frac{\mathrm{sen}\ [2\varphi(t)]}{\sqrt{2}}\ \big(-\vec{\imath}\ +\ \vec{\jmath}\!\ \big)\!\ +\!\ \cos [2\varphi(t)]\ \vec{k}\end{array}\right.](/wiki/images/math/9/f/7/9f7d57a8c6529f8953a71cd4b594f57d.png)
2.2 Expresiones de la aceleración instantánea
La aceleración instantánea de una partícula se define como la variación que por unidad de tiempo experimenta el vector velocidad instantánea. La expresión analítica de dicha magnitud vectorial se obtiene derivando con respecto al tiempo la expresión horaria de la velocidad:
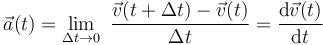
- Coordenadas cartesianas
Si tenemos la velocidad instantánea de la partícula expresada analíticamente en términos de la base cartesiana  , con sus componentes como funciones del tiempo, las derivadas temporales de dichas componentes serán las componentes cartesianas de la aceleración instantánea.
, con sus componentes como funciones del tiempo, las derivadas temporales de dichas componentes serán las componentes cartesianas de la aceleración instantánea.
En el sistema bajo estudio hemos obtenido una expresión de la velocidad instantánea en terminos de la posición que ocupa la partícula en un cierto instante, dada por el valor de la variable geométrica  . Por tanto, para obtenter la expresión cartesiana de la aceleración, podemos aplicar de nuevo la regla e la cadena:
. Por tanto, para obtenter la expresión cartesiana de la aceleración, podemos aplicar de nuevo la regla e la cadena:
![\vec{a}(t)=\frac{\mathrm{d}\vec{v}(t)}{\mathrm{d}t}=\frac{\mathrm{d}\vec{v}[\varphi(t)]}{\mathrm{d}t}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}\varphi}\ \frac{\mathrm{d}\varphi}{\mathrm{d}t}\mathrm{;}\,\;\;\,\mathrm{siendo}\,\;\;\left\{\begin{array}{l}\displaystyle \frac{\mathrm{d}\vec{v}}{\mathrm{d}\varphi}= 2\!\ \omega_0\!\ b\!\ \bigg(-\mathrm{cos}\ 2\!\ \varphi \ \vec{\imath}+\ \mathrm{cos}\ 2\!\ \varphi\ \vec{\jmath}\!\ -\sqrt{2}\ \mathrm{sen}\ 2\!\ \varphi\ \vec{k}\bigg) \\ \\ \displaystyle \frac{\mathrm{d}\varphi}{\mathrm{d}t}=\omega_0\mathrm{,}\,\;\;\mathrm{cte.}\end{array}\right.](/wiki/images/math/a/1/8/a18becb4847c82b8b20fe9cae9773a23.png)
Y combinando ambas derivadas se obtiene la expresión analítica de la aceleración en la base cartesiana, como una función del tiempo y de la posición de la partícula en cada instante de tiempo:
![\vec{a}[\varphi(t)]=2\!\ \omega_0^2\!\ b \!\ \bigg[-\mathrm{cos}\ 2\!\ \varphi(t)
\ \vec{\imath}+\ \mathrm{cos}\ 2\!\ \varphi(t)\ \vec{\jmath}\!\ -\sqrt{2}\ \mathrm{sen}\ 2\!\ \varphi(t)\ \vec{k}\bigg]=a_x(t)\ \vec{\imath}\!\ + \!\ a_y(t)\ \vec{\jmath}\!\ + \ a_z(t)\!\ \vec{k}\mathrm{;}\;\;\;\,\mathrm{siendo}\;\;\; \left\{\begin{array}{l} a_x(t)=\ddot{x}(t)=-2\!\ \omega_0^2\!\ b\,\mathrm{cos}\!\ (2\!\ \omega_0\!\ t)\\ \\ a_y(t)=\ddot{y}(t)=2\!\ \omega_0^2\!\ b\,\mathrm{cos}\!\ (2\!\ \omega_0^2\!\ t)\\ \\ \displaystyle a_z(t)=\ddot{z}(t)=-2\!\ \sqrt{2}\!\ \omega_0^2\!\ b \,\mathrm{sen}\!\ (2\!\ \omega_0\!\ t)\end{array}\right.](/wiki/images/math/5/a/2/5a217d6d05c6db3fbe4d43aef1958943.png)
- Componentes intrínsecas
![\overrightarrow{OP}=\vec{r} (t)\mathrm{,}\quad\mathrm{tal}\;\;\mathrm{que}\;\;\,\vec{v}(t)=v(t)\!\ \vec{T}[P(t)] \; \Longrightarrow \; \vec{a} (t)=\ \frac{\mathrm{d}\vec{v}(t)}{\mathrm{d}t}=\ \frac{\mathrm{d}v(t)}{\mathrm{d}t}\ \vec{T} \!\ + \!\ v(t)\ \frac{\mathrm{d}\vec{T}}{\mathrm{d}t}\bigg\rfloor_{P(t)}](/wiki/images/math/4/a/6/4a6bf59a87cb03f6d0d20f207a217d5a.png)
El vector normal  es el vector unitario cuya dirección y sentido coinciden con los de la variación que sufre el vector tangente a la trayectoria, cuando la partícula se desplaza desde la posición
es el vector unitario cuya dirección y sentido coinciden con los de la variación que sufre el vector tangente a la trayectoria, cuando la partícula se desplaza desde la posición  a la inmediatamente posterior,
a la inmediatamente posterior,  . Por tanto, la aceleración instantánea de una partícula en movimiento, expresada en el triedro intrínseco, tendrá dos componentes, en general: una en la dirección del vector tangente, denominada aceleración tangencial, y otra en la dirección del vector normal, llamada por eso aceleración normal:
. Por tanto, la aceleración instantánea de una partícula en movimiento, expresada en el triedro intrínseco, tendrá dos componentes, en general: una en la dirección del vector tangente, denominada aceleración tangencial, y otra en la dirección del vector normal, llamada por eso aceleración normal:
![\vec{N}(P)\,\|\, \mathrm{d}\vec{T}=\vec{T}[P(t+\mathrm{d}t)]-\vec{T}[P(t)]\quad\Longrightarrow
\vec{a} (t)=a_{{}_T}\!\ \vec{T}(P)\!\ + \!\ a_{{}_N}\!\ \vec{N}(P)](/wiki/images/math/e/f/6/ef6192756f978850d9e86479cd4ab1ee.png)
La componente tangencial  , da cuenta de la variación por unidad de tiempo de la celeridad (es decir, del módulo de la velocidad). La componente normal
, da cuenta de la variación por unidad de tiempo de la celeridad (es decir, del módulo de la velocidad). La componente normal  , describe cómo cambia la dirección de la velocidad por unidad de tiempo; como se sabe, ésta componente depende de la celeridad instantánea de la partícula y de una propiedad geométrica de la trayectoria llamada curvatura
, describe cómo cambia la dirección de la velocidad por unidad de tiempo; como se sabe, ésta componente depende de la celeridad instantánea de la partícula y de una propiedad geométrica de la trayectoria llamada curvatura  (o de su inversa: el radio de curvatura
(o de su inversa: el radio de curvatura 
![\vec{a}(t)=a_{{}_T}\!\ \vec{T}(P)\!\ + \!\ a_{{}_N}\!\ \vec{N}(P)=\frac{\mathrm{d}v(t)}{\mathrm{d}t}\ \vec{T} [P(t)]\!\ + \!\ v^2(t)\!\ \kappa (P)\!\ \vec{N} [P(t)]\mathrm{,}\quad\forall\,P\in\Gamma](/wiki/images/math/9/9/6/996dfc7bb70364c0d5c90718f1bb24a2.png)
Procedamos a calcular las componentes intrínsecas de la aceleración instantánea en el movimiento bajo estudio. En el caso de la componente tangencial...
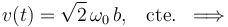
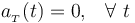
En consecuencia, la aceleración instantánea de la partícula es, en todo momento, exclusivamente normal a la trayectoria. Así, a partir de la expresión analítica cartesiana de esta magnitud vectorial, podemos determinar tanto la componente normal como el vector unitario normal a la trayectoria, para cada posición instantánea de la partícula:
![\vec{a}[\varphi(t)]=2\!\ \omega_0^2\!\ b \!\ \bigg[-\mathrm{cos}\ 2\!\ \varphi(t)
\ \vec{\imath}+\ \mathrm{cos}\ 2\!\ \varphi(t)\ \vec{\jmath}\!\ -\sqrt{2}\ \mathrm{sen}\ 2\!\ \varphi(t)\ \vec{k}\bigg]= a_{{}_N}(t)\!\ \vec{N} [\varphi]\; \;\Longrightarrow](/wiki/images/math/0/1/8/018f0baf46dcc925e732eba968082310.png)
![\begin{array}{l} \displaystyle a_{{}_N}(t)=|\vec{a}(t)|=2\!\ \sqrt{2}\!\ \omega_0^2\!\ b\mathrm{,}\quad\mathrm{cte.}\\ \\ \displaystyle \vec{N}[P(\varphi)]=\frac{\vec{a}(t)}{|\vec{a}(t)|}=\frac{ \mathrm{cos}\ [2\varphi(t)]}{\sqrt{2}}\ \big(-\vec{\imath}\ +\ \vec{\jmath}\!\ \big)\!\ -\!\ \mathrm{sen}\ [2\varphi(t)]\ \vec{k} \end{array}](/wiki/images/math/e/d/0/ed081dbf8197d853da5db1e2c034fc30.png)
3 Ley horaria para el parámetro arco
Como se comentó anteriormente, el vector desplazamiento elemental 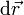 queda definido por la posición de la partícula en un cierto instante, y otra en un instante inmediatamente posterior. Por tanto,
queda definido por la posición de la partícula en un cierto instante, y otra en un instante inmediatamente posterior. Por tanto, sería la distancia recorrida por la partícula entre esas dos posiciones inifinitamente próximas. Entonces...
sería la distancia recorrida por la partícula entre esas dos posiciones inifinitamente próximas. Entonces...
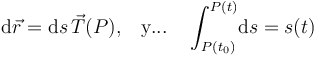
donde 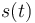 es la distancia recorrida por la partícula entre el instante inicial t0 y el instante t o, lo que es lo mismo, la distancia entre los puntos P0 y P, medida a lo largo de la trayectoria. Esta magnitud física escalar se denomina parámetro arco. La relación de éste con la celeridad de la partícula es fácil de determinar:
es la distancia recorrida por la partícula entre el instante inicial t0 y el instante t o, lo que es lo mismo, la distancia entre los puntos P0 y P, medida a lo largo de la trayectoria. Esta magnitud física escalar se denomina parámetro arco. La relación de éste con la celeridad de la partícula es fácil de determinar:
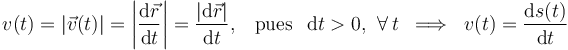
Consideremos que en el sistema bajo estudio, la partícula se encuentra en el instante inicialt0 = 0 en una determinada posición P0. La distancia recorrida hasta la posición P(t) que ocupa en un instante posterior será: