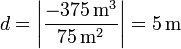No Boletín - Cálculo de distancia entre dos rectas

De Laplace

1 Enunciado

Sean las rectas $r 1$ , que pasa por los puntos $A ( - 2,5,1)$ y $B (7, - 7,1)$ , y $r 2$ que pasa por $C (5,4, - 3)$ y $D (5,4,2)$ (todas las unidades en el SI). Empleando el álgebra vectorial, determine la distancia entre estas dos rectas.

2 Solución

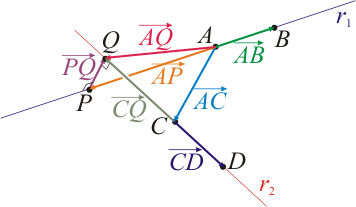
La distancia entre dos rectas es la correspondiente a la que hay entre los puntos más próximos de una y de otra. Estos dos puntos se encuentran sobre la perpendicular común a ambas rectas.

Se trata entonces de hallar la distancia entre dos puntos $P$ y $Q$ tales que $P$ pertenece a $r 1$ , $Q$ pertenece a $r 2$ y 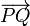$\overrightarrow{PQ}$ es ortogonal a los vectores directores de ambas rectas.

Si $P$ pertenece a la recta $r 1$ , se cumple

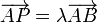
$\overrightarrow{AP}=\lambda\overrightarrow{AB}$

y si $Q$ pertenece a $r 2$

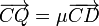
$\overrightarrow{CQ}=\mu\overrightarrow{CD}$

El vector de posición relativo entre ambos puntos será

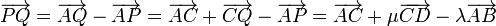
$\overrightarrow{PQ}=\overrightarrow{AQ}-\overrightarrow{AP}=\overrightarrow{AC}+\overrightarrow{CQ}-\overrightarrow{AP}=\overrightarrow{AC}+\mu\overrightarrow{CD}-\lambda\overrightarrow{AB}$

Este vector debe ser ortogonal tanto al vector 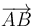$\overrightarrow{AB}$ como al vector 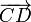$\overrightarrow{CD}$ y por tanto será paralelo al producto vectorial de ambos

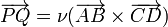
$\overrightarrow{PQ}=\nu(\overrightarrow{AB}\times\overrightarrow{CD})$

La distancia entre las rectas será el módulo de este vector

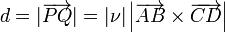
$d = |\overrightarrow{PQ}| = |\nu|\left|\overrightarrow{AB}\times\overrightarrow{CD}\right|$

Por tanto, solo necesitamos hallar el parámetro $ν$ . Igualando las dos expresiones para el vector $\overrightarrow{PQ}$

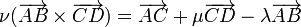
$\nu(\overrightarrow{AB}\times\overrightarrow{CD}) = \overrightarrow{AC}+\mu\overrightarrow{CD}-\lambda\overrightarrow{AB}$

Multiplicando escalarmente por 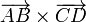$\overrightarrow{AB}\times\overrightarrow{CD}$ nos queda simplemente

$\nu \left|\overrightarrow{AB}\times\overrightarrow{CD}\right|^2 = \overrightarrow{AC}\cdot(\overrightarrow{AB}\times\overrightarrow{CD})$

y por tanto la distancia que buscamos es

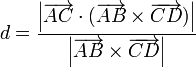
$d = \frac{\left|\overrightarrow{AC}\cdot(\overrightarrow{AB}\times\overrightarrow{CD})\right|}{\left|\overrightarrow{AB}\times\overrightarrow{CD}\right|}$

Nótese que el resultado final no requiere localizar los puntos $P$ y $Q$ sino que hemos llegado a una expresión para la distancia que solo depende de los cuatro puntos dados.

Sustituyendo los valores tenemos

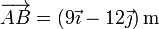
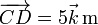
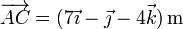
$\overrightarrow{AB}=(9\vec{\imath}-12\vec{\jmath})\,\mathrm{m}$ $\overrightarrow{CD}=5\vec{k}\,\mathrm{m}$ $\overrightarrow{AC}=(7\vec{\imath}-\vec{\jmath}-4\vec{k})\,\mathrm{m}$

Hallando los productos vectoriales y mixto

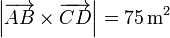
$\overrightarrow{AB}\times\overrightarrow{CD}=\left(-60\vec{\imath}-45\vec{\jmath}\right)\,\mathrm{m}^2$ $\left|\overrightarrow{AB}\times\overrightarrow{CD}\right| = 75\,\mathrm{m}^2$ $\overrightarrow{AC}\cdot(\overrightarrow{AB}\times\overrightarrow{CD}) = -375\,\mathrm{m}^3$

por lo que la distancia entre las rectas es

$d = \left|\frac{-375\,\mathrm{m}^3}{75\,\mathrm{m}^2}\right|=5\,\mathrm{m}$

No Boletín - Cálculo de distancia entre dos rectas

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES