No Boletín - Sistema de ecuaciones vectoriales

De Laplace

Contenido

1 Enunciado
2 Introducción
3 Propiedades cancelativas
4 Solución geométrica
5 Doble producto vectorial

1 Enunciado

Demuestre que si se cumplen simultáneamente las condiciones

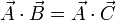
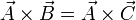
$\vec{A}\cdot\vec{B} = \vec{A}\cdot\vec{C}$ $\vec{A}\times\vec{B} = \vec{A}\times\vec{C}$

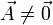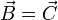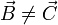siendo $\vec{A}\neq \vec{0}$ , entonces $\vec{B} = \vec{C}$ ; pero si se cumple una de ellas y la otra no, entonces $\vec{B}\neq\vec{C}$ .

2 Introducción

Existen varias formas de abordar este problema:

Empleando las propiedades cancelativas.
Mediante argumentos geométricos.
Empleando el doble producto vectorial.

Veremos cada uno de estos tres métodos por separado.

3 Propiedades cancelativas

Si en la igualdad de los productos vectoriales pasamos todo al primer miembro nos queda

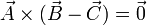
$\vec{A}\times(\vec{B}-\vec{C})=\vec{0}$

Esto quiere decir que el vector 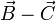$\vec{B}-\vec{C}$ es paralelo al vector $\vec{A}$ (pudiendo también ser nula la diferencia). Por ello puede escribirse

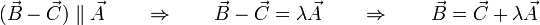
$(\vec{B}-\vec{C})\parallel\vec{A}\qquad\Rightarrow\qquad \vec{B}-\vec{C}=\lambda\vec{A}\qquad\Rightarrow\qquad \vec{B}=\vec{C}+\lambda\vec{A}$

Si ahora multiplicamos escalarmente este resultado por $\vec{A}$ nos queda

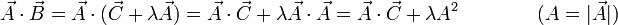
$\vec{A}\cdot\vec{B} = \vec{A}\cdot(\vec{C}+\lambda\vec{A}) = \vec{A}\cdot\vec{C}+\lambda \vec{A}\cdot\vec{A}=\vec{A}\cdot\vec{C}+\lambda A^2\qquad\qquad (A = |\vec{A}|)$

Pero, al ser también iguales los productos escalares

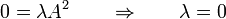
$0 = \lambda A^2\qquad \Rightarrow\qquad \lambda=0$

ya que el módulo de $\vec{A}$ no es nulo. Por tanto

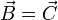
$\vec{B}=\vec{C}$

Si el producto escalar no es coincidente, ya esta igualdad no se cumple

$\vec{A}\cdot\vec{B}\neq\vec{A}\cdot\vec{C} \qquad\Rightarrow\qquad 0 \neq \lambda A^2\qquad\Rightarrow\qquad \lambda\neq 0\qquad\Rightarrow\qquad \vec{B}\neq\vec{C}$

Si no coinciden los productos vectoriales

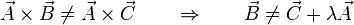
$\vec{A}\times\vec{B}\neq\vec{A}\times\vec{C} \qquad\Rightarrow\qquad \vec{B} \neq \vec{C}+ \lambda \vec{A}$

Multiplicando aquí escalarmente por $\vec{A}$

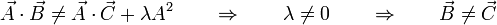
$\vec{A}\cdot\vec{B}\neq \vec{A}\cdot\vec{C}+\lambda A^2 \qquad\Rightarrow\qquad \lambda\neq 0\qquad\Rightarrow\qquad \vec{B}\neq\vec{C}$

4 Solución geométrica

Consideremos que $\vec{B}$ y $\vec{C}$ representan vectores de posición de dos puntos $B$ y $C$ respecto a un cierto origen de coordenadas fijo. En ese caso la ecuación vectorial

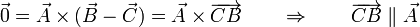
$\vec{0}=\vec{A}\times(\vec{B}-\vec{C}) = \vec{A}\times\overrightarrow{CB}\qquad\Rightarrow\qquad \overrightarrow{CB} \parallel \vec{A}$

Esto quiere decir que el vector que une los puntos $B$ y $C$ va en la dirección de $\vec{A}$ o, geométricamente, que $B$ se encuentra sobre una recta que pasa por $C$ y va en la dirección de $\vec{A}$ (ecuación vectorial de la recta).

Por otro lado, de la igualdad de productos escalares

$0 = \vec{0}=\vec{A}\cdot(\vec{B}-\vec{C}) = \vec{A}\cdot\overrightarrow{CB}\qquad\Rightarrow\qquad \overrightarrow{CB} \perp \vec{A}$

Este resultado nos dice que el vector que une los puntos $C$ y $B$ es perpendicular al vector $\vec{A}$ y por tanto $B$ se encuentra en un plano que pasa por $C$ y tiene por vector normal a $\vec{A}$ (ecuación vectorial del plano).

Ahora bien, dado que ambas ecuaciones se cumplen simultáneamente, tenemos que $B$ se encuentra en la intersección de una recta que pasa por $C$ y un plano que pasa por $C$ , siendo la recta normal al plano. La única intersección posible es el propio punto $C$ , ambos puntos son el mismo y

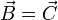
$\vec{B}=\vec{C}$

Inversamente, si alguna de las igualdades no se cumple, entonces $B$ no se encuentra sobre la recta o no se encuentra sobre el plano, y no puede coincidir con el punto $C$ , por lo que los vectores son diferentes.

5 Doble producto vectorial

Veamos primero una propiedad general. Si multiplicamos un vector $\vec{B}$ por un vector $\vec{A}$ y al resultado lo volvemos a multiplicar por el mismo vector $\vec{A}$ , el resultado es, aplicando las propiedades del doble producto vectorial

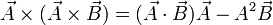
$\vec{A}\times(\vec{A}\times\vec{B}) = (\vec{A}\cdot\vec{B})\vec{A} - A^2\vec{B}$

Del segundo miembro podemos despejar el vector $\vec{B}$ , ya que el módulo de $\vec{A}$ es no nulo

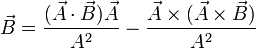
$\vec{B} = \frac{(\vec{A}\cdot\vec{B})\vec{A}}{A^2} - \frac{\vec{A}\times(\vec{A}\times\vec{B})}{A^2}$

En esta expresión, el primer término del segundo miembro va en la dirección de $\vec{A}$ , mientras que el segundo es ortogonal a este vector. Por ello esta fórmula nos da la descomposición de un vector en sus componentes paralela y normal a otro (como se hace, por ejemplo, al hallar las componentes intrínsecas de la aceleración).

Aplicando esta misma fórmula al vector $\vec{C}$ en lugar de $\vec{B}$ obtenemos

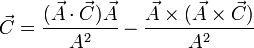
$\vec{C} = \frac{(\vec{A}\cdot\vec{C})\vec{A}}{A^2} - \frac{\vec{A}\times(\vec{A}\times\vec{C})}{A^2}$

pero, de acuerdo con el enunciado,

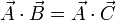
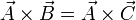
$\vec{A}\cdot\vec{B}=\vec{A}\cdot\vec{C}$ $\vec{A}\times\vec{B}=\vec{A}\times\vec{C}$

por lo que, sustituyendo, nos queda

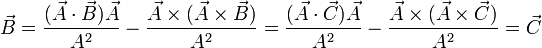
$\vec{B} = \frac{(\vec{A}\cdot\vec{B})\vec{A}}{A^2} - \frac{\vec{A}\times(\vec{A}\times\vec{B})}{A^2}=\frac{(\vec{A}\cdot\vec{C})\vec{A}}{A^2} - \frac{\vec{A}\times(\vec{A}\times\vec{C})}{A^2}=\vec{C}$

Y los dos vectores son iguales. Geométricamente, las identidades del enunciado conducen a que son iguales las componentes paralelas y normales a $\vec{A}$ y dos vectores son iguales si y solo si son iguales sus componentes.

Inversamente si alguno de los dos productos son diferentes, los vectores se diferenciarán o bien en su componente paralela o bien en su componente normal y por tanto no podrán ser iguales.

No Boletín - Sistema de ecuaciones vectoriales

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Propiedades cancelativas

4 Solución geométrica

5 Doble producto vectorial

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES