No Boletín - Identificación de lugar geométrico (Ex.Nov/16)
De Laplace
1 Enunciado
Sea  la recta que pasa por el punto
la recta que pasa por el punto 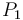 y es paralela al vector
y es paralela al vector 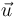 , y sea
, y sea  un punto que no pertenece a
un punto que no pertenece a  .
.
¿Cuál es el lugar geométrico de los puntos  que satisfacen la ecuación
que satisfacen la ecuación  ?
?
2 Solución
Como aplicación del producto escalar de vectores, se ha estudiado en la teoría que la ecuación del plano perpendicular al vector  y que pasa por el punto
y que pasa por el punto  viene dada por:
viene dada por:
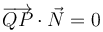
Pues bien, la ecuación que nos propone el enunciado del presente ejercicio se reduce a esta forma mediante una sencilla operación de resta:
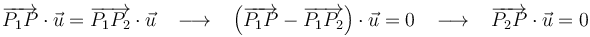
Por tanto, el lugar geométrico de los puntos  que satisfacen dicha ecuación es el plano perpendicular a la recta
que satisfacen dicha ecuación es el plano perpendicular a la recta  y que pasa por el punto
y que pasa por el punto  (nótese que
(nótese que  es paralela a
es paralela a 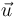 ).
).
3 Solución alternativa
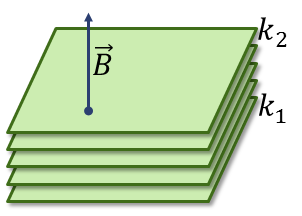
La ecuación vectorial de un plano perpendicular al vector  es de la forma general
es de la forma general
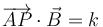
siendo A un punto fijo y k una constante. Tomando distintos valores de k obtenemos planos paralelos.
En nuestro caso la ecuación tiene esta forma si tomamos 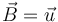 . Es decir se trata de un plano perpendicular al vector
. Es decir se trata de un plano perpendicular al vector  y por tanto a la recta r.
y por tanto a la recta r.
Para hallar un punto de este plano simplemente observamos que la ecuación se cumple para P = P2 ya que trivialmente
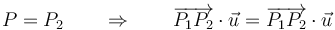
Por tanto, se trata de un plano perpendicular a la recta r y que pasa por el punto P2.