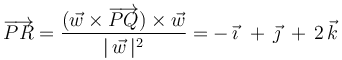No Boletín - Camino más corto entre un punto y una recta (Ex.Oct/14)

De Laplace

1 Enunciado

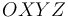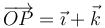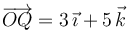En un sistema cartesiano $OXYZ\,$ se define el punto $P\,$ (de posición $\overrightarrow{OP}=\vec{\imath}+\vec{k}\,$ ) y la recta $r\,$ (que pasa por el punto $Q\,$ de posición $\overrightarrow{OQ}=3\,\vec{\imath}+5\,\vec{k}\,$ , y es paralela al vector 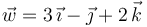$\vec{w}=3\,\vec{\imath}-\vec{\jmath}+2\,\vec{k}\,$ ). Determine el vector que coincide con el camino más corto que lleva desde el punto $P\,$ hasta la recta $r\,$ .

2 Solución

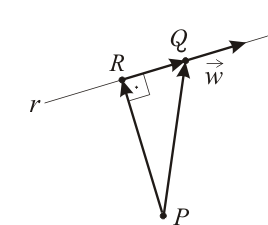
El camino más corto que lleva desde el punto $P\,$ hasta la recta $r\,$ coincide con un vector ortogonal a $r\,$ que tiene su origen en $P\,$ y su extremo en un punto de $r\,$ (punto al que llamaremos $R\,$ ). Por tanto, nuestro objetivo en este ejercicio consiste en calcular dicho vector 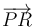$\overrightarrow{PR}\,$ .

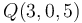Sabemos que la recta $r\,$ pasa por el punto $Q(3,0,5)\,$ y admite como vector director a 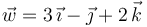$\vec{w}=3\,\vec{\imath}-\vec{\jmath}+2\,\vec{k}\,$ . Por tanto, las coordenadas de un punto genérico de dicha recta (ecuaciones $λ$ -paramétricas de $r\,$ ) son:

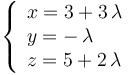
$\left\{\begin{array}{l} x=3+3\,\lambda \\ y=-\,\lambda \\ z=5+2\,\lambda \end{array}\right.$

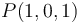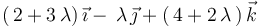Si a las coordenadas de este punto genérico de $r\,$ les restamos las coordenadas del punto $P(1,0,1)\,$ , deducimos que el vector que va desde $P\,$ hasta un punto genérico de $r\,$ vale $(\,2+3\,\lambda)\,\vec{\imath}-\,\lambda\,\vec{\jmath}+(\,4+2\,\lambda\,)\,\vec{k}\,$ .

Finalmente, determinamos el vector 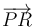$\overrightarrow{PR}\,$ exigiendo su ortogonalidad a $r\,$ y, por tanto, al vector 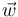$\vec{w}\,$ :

$\overrightarrow{PR}\perp\vec{w}\,\,\,\rightarrow\,\,\,\overrightarrow{PR}\,\cdot\,\vec{w}=\left[\,(\,2+3\,\lambda)\,\vec{\imath}-\,\lambda\,\vec{\jmath}+(\,4+2\,\lambda\,)\,\vec{k}\,\right]\,\cdot\left(\,3\,\vec{\imath}-\vec{\jmath}+2\,\vec{k}\,\right)=14\,\lambda\,+\,14=0\,\,\,\rightarrow\,\,\,\lambda=-\,1\,\,\,\rightarrow\,\,\,\overrightarrow{PR}=-\,\vec{\imath}\,\,+\,\vec{\jmath}\,\,+\,2\,\vec{k}$

3 Procedimiento alternativo

Un procedimiento alternativo consiste en descomponer el vector 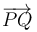$\overrightarrow{PQ}\,$ como la suma de dos vectores: uno perpendicular a 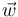$\vec{w}\,$ y otro paralelo a 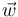$\vec{w}\,$ (en la teoría se ha deducido una fórmula para este tipo de descomposición), y a continuación darse cuenta de que el vector 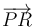$\overrightarrow{PR}\,$ buscado coincide precisamente con el vector perpendicular a 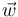$\vec{w}\,$ de la citada descomposición:

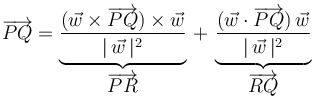
$\overrightarrow{PQ}=\underbrace{\frac{(\vec{w}\times\overrightarrow{PQ})\times\vec{w}}{|\,\vec{w}\,|^2}}_{\overrightarrow{PR}}\,+\,\underbrace{\frac{(\vec{w}\cdot\overrightarrow{PQ})\,\vec{w}}{|\,\vec{w}\,|^2}}_{\overrightarrow{RQ}}$

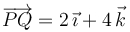Así que, restando las coordenadas de $P\,$ a las coordenadas de $Q\,$ , determinamos el vector $\overrightarrow{PQ}=2\,\vec{\imath}+4\,\vec{k}\,$ ; y, aplicando la fórmula correspondiente, obtenemos: