No Boletín - Cálculo de una diagonal (Ex.Ene/13)

De Laplace

1 Enunciado

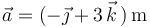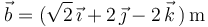Sea el rombo cuyos lados quedan definidos por los vectores $\vec{a}=(-\vec{\jmath}+3\,\vec{k}\,)\,\mathrm{m}\,$ y $\vec{b}=(\sqrt{2}\,\vec{\imath}+2\,\vec{\jmath}-2\,\vec{k}\,)\,\mathrm{m}\,$ . ¿Cuál es la longitud de su diagonal mayor?

2 Solución

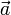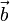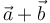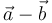Si $\vec{a}\,$ y $\vec{b}\,$ definen los lados de un rombo, es trivial comprobar (por las definiciones geométricas de suma y resta de vectores) que las diagonales del rombo vienen dadas por los vectores $\vec{a}+\vec{b}\,$ y $\vec{a}-\vec{b}\,$ :

$\vec{a}+\vec{b}=(\sqrt{2}\,\,\vec{\imath}+\vec{\jmath}+\vec{k}\,)\,\mathrm{m}\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}-\vec{b}=(-\sqrt{2}\,\,\vec{\imath}-3\,\vec{\jmath}+5\,\vec{k}\,)\,\mathrm{m}$

Las longitudes de las diagonales se calculan tomando módulos:

$|\vec{a}+\vec{b}\,|=2\,\mathrm{m}\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, |\vec{a}-\vec{b}\,|=6\,\mathrm{m}$

Y, comparando las dos longitudes, comprobamos que la diagonal mayor es la que mide 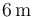$6\,\mathrm{m}\,$ .

Cabe señalar que el ejercicio se resolvería del mismo modo para un paralelogramo arbitrario. El hecho de que se trate particularmente de un rombo no ha tenido relevancia alguna en el procedimiento. No obstante, podemos comprobar por gusto que en efecto se trata de un rombo, es decir, que sus lados tienen la misma longitud y no son ortogonales:

$|\vec{a}|=|\vec{b}\,|=\sqrt{10}\,\,\mathrm{m}\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}\cdot\vec{b}\neq 0$

No Boletín - Cálculo de una diagonal (Ex.Ene/13)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES