No Boletín - Identificación de lugar geométrico II (Ex.Oct/18)
De Laplace
1 Enunciado
Sea  la recta que pasa por el punto
la recta que pasa por el punto 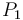 y es paralela al vector
y es paralela al vector 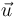 , y sea
, y sea  un punto que no pertenece a
un punto que no pertenece a  . Responda a la siguiente pregunta aplicando la propiedad cancelativa del producto vectorial.
. Responda a la siguiente pregunta aplicando la propiedad cancelativa del producto vectorial.
¿Cuál es el lugar geométrico de los puntos  que satisfacen la ecuación
que satisfacen la ecuación 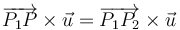 ?
?
2 Solución
Aplicando la propiedad cancelativa del producto vectorial, se deduce que:

y mediante una sencilla operación de resta:
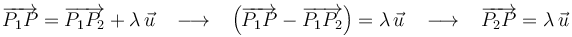
El paralelismo de los vectores 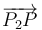 y
y 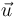 (relacionados mediante el factor escalar paramétrico
(relacionados mediante el factor escalar paramétrico 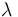 ) implica que
) implica que  se halla necesariamente en la recta paralela a
se halla necesariamente en la recta paralela a 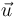 que pasa por
que pasa por  .
.
Por tanto, el lugar geométrico de los puntos  que satisfacen la ecuación dada en la pregunta del enunciado es la recta paralela a la recta
que satisfacen la ecuación dada en la pregunta del enunciado es la recta paralela a la recta  que pasa por el punto
que pasa por el punto  (nótese que
(nótese que  es paralela a
es paralela a 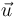 ).
).





