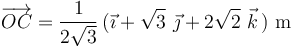No Boletín - Arista de un tetraedro II (Ex.Oct/15)
De Laplace
1 Enunciado
Los puntos  ,
,  ,
,  y
y 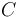 son los vértices de un tetraedro regular cuyas caras son triángulos equiláteros con lados de longitud igual a
son los vértices de un tetraedro regular cuyas caras son triángulos equiláteros con lados de longitud igual a 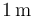 . Se elige el triedro cartesiano
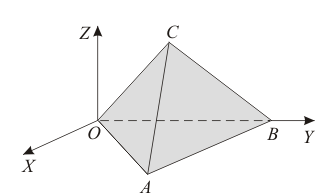
. Se elige el triedro cartesiano 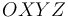 de la figura, de tal modo que las aristas
de la figura, de tal modo que las aristas 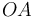 y
y 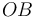 del tetraedro quedan definidas por los vectores:
del tetraedro quedan definidas por los vectores:
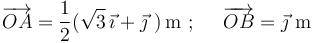
Determine el vector 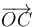 , por el que queda definida la arista
, por el que queda definida la arista 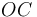 del tetraedro.
del tetraedro.
2 Solución
Por comodidad, prescindiremos de las unidades hasta llegar a la solución final (son todas unidades del SI). Sabemos que todas las caras del tetraedro son triángulos equiláteros con lados de longitud igual a 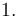 Así que
Así que 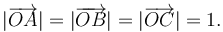 Y sabemos que los ángulos internos de un triángulo equilátero valen
Y sabemos que los ángulos internos de un triángulo equilátero valen 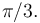 Todo esto nos permite calcular el valor de los siguientes productos escalares (por definición):
Todo esto nos permite calcular el valor de los siguientes productos escalares (por definición):
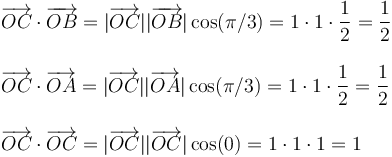
Conocemos en base cartesiana los vectores 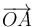 y
y 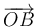 , y queremos determinar el vector
, y queremos determinar el vector 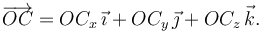
Realizando los productos escalares anteriores a partir de las componentes cartesianas de los correspondientes vectores, y exigiendo que los resultados así obtenidos coincidan con los valores antes obtenidos por definición, determinamos las componentes cartesianas de 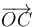 :
:
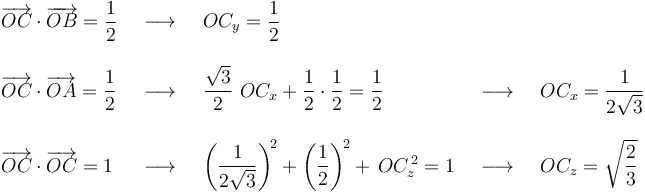
habiéndose elegido la raíz positiva (y descartado la negativa) como solución de 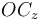 por coherencia con la figura del enunciado.
por coherencia con la figura del enunciado.
Asi que: