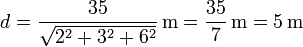1.5. Ejemplo de ecuación vectorial de un plano

De Laplace

1 Enunciado

Obtenga la ecuación del plano perpendicular al vector libre 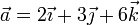$\vec{a}= 2\vec{\imath}+3\vec{\jmath}+6\vec{k}$ y que contiene a un punto $P$ , cuya posición respecto del origen de un sistema de referencia $O X Y Z$ viene dada por el radiovector 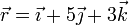$\vec{r} = \vec{\imath} + 5\vec{\jmath} + 3\vec{k}$ . Calcule la distancia que separa a dicho plano del origen $O$ . (Unidades del SI)

2 Ecuación del plano

La propiedad que caracteriza a cada punto Q del plano es que el vector que va del punto $P$ al $Q$ es ortogonal al vector normal al plano, esto es,

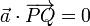
$\vec{a}\cdot\overrightarrow{PQ} = 0$

Si el vector de posición del punto $Q$ respecto al origen es

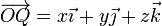
$\overrightarrow{OQ}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}$

el vector de posición relativo al punto $P$ es (midiendo todas las distancias en metros)

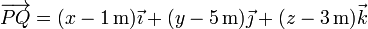
$\overrightarrow{PQ}=(x-1\,\mathrm{m})\vec{\imath}+(y-5\,\mathrm{m})\vec{\jmath}+(z-3\,\mathrm{m})\vec{k}$

La condición de ortogonalidad al vector normal al plano la podemos desarrollar escribiendo el producto escalar como suma de productos de componentes

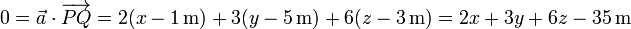
$0 = \vec{a}\cdot\overrightarrow{PQ}=2(x-1\,\mathrm{m}) + 3(y-5\,\mathrm{m}) + 6(z-3\,\mathrm{m}) = 2x + 3y + 6z -35\,\mathrm{m}$

lo que nos da la ecuación implícita del plano

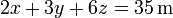
$2x + 3y + 6z = 35\,\mathrm{m}$

Alternativamente, podemos llegar a esta ecuación imponiendo que

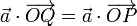
$\vec{a}\cdot\overrightarrow{OQ} = \vec{a}\cdot\overrightarrow{OP}$

que, geométricamente, significa que para cada punto del plano tiene el mismo valor la proyección de su vector de posición sobre el vector $\vec{a}$ .

3 Distancia al origen

La distancia de un punto O a un plano Π, se toma como la mínima de las distancias de O a los diferentes puntos del plano. El punto que se encuentra a la mínima distancia es el que se halla en la intersección del plano con la recta normal a él que pasa por O. Sea A este punto de intersección. Se cumple entonces

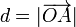
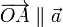
$d = |\overrightarrow{OA}|$ $\overrightarrow{OA}\parallel\vec{a}$

Esta distancia coincide con el valor absoluto de la proyección del vector $\overrightarrow{OA}$ sobre el vector $\vec{a}$

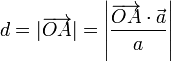
$d = |\overrightarrow{OA}| = \left|\frac{\overrightarrow{OA}\cdot\vec{a}}{a}\right|$

pero hemos dicho antes que la proyección sobre este vector es la misma para todos los puntos del plano, esto es, que no precisamos determinar la posición del punto A, sino que cualquier otro punto del plano nos vale para calcular esta distancia. Por ejemplo, el punto P que ya conocemos

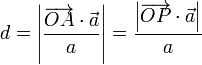
$d = \left|\frac{\overrightarrow{OA}\cdot\vec{a}}{a}\right|= \frac{\left|\overrightarrow{OP}\cdot\vec{a}\right|}{a}$

Sustituyendo los valores

$d = \frac{35}{\sqrt{2^2+3^2+6^2}}\,\mathrm{m}= \frac{35}{7}\,\mathrm{m} = 5\,\mathrm{m}$

1.5. Ejemplo de ecuación vectorial de un plano

De Laplace

1 Enunciado

2 Ecuación del plano

3 Distancia al origen

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES