No Boletín - Volumen de un paralelepípedo II (Ex.Oct/14)
De Laplace
1 Enunciado
Sea 
el ángulo formado por dos vectores libres 
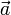y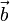 
. ¿Cuál es el volumen del paralelepípedo cuyas aristas vienen definidas por la terna 
?
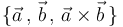2 Solución
El volumen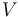 
de un paralelepípedo es igual al valor absoluto del producto mixto de los tres vectores-aristas que definen el paralelepípedo. Así que, en este caso, tendremos:
![V=\left|\,\vec{a}\cdot\left[\,\vec{b}\times\left(\vec{a}\times\vec{b}\,\right)\right]\right|](/wiki/images/math/0/b/f/0bf0329122690ed7f6f5f2e4b70ce962.png)
Pero desarrollando el doble producto vectorial que aparece entre corchetes, llegamos a:
![V=\left|\,\vec{a}\cdot\left[(\vec{b}\cdot\vec{b}\,)\,\vec{a}-(\vec{b}\cdot\vec{a}\,)\,\vec{b}\,\right]\right|](/wiki/images/math/0/2/6/026c4cc377a5e147afe0caa53954c1c1.png)
Aplicando la propiedad distributiva del producto escalar respecto a la suma de vectores para eliminar los corchetes, y teniendo en cuenta que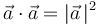 
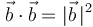, que 
y que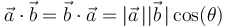 
, obtenemos:
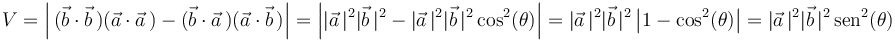
Al mismo resultado se llega de forma más rápida si se utiliza la propiedad de permutabilidad cíclica del producto mixto de partida:
![V=\left|\,\vec{a}\cdot\left[\,\vec{b}\times\left(\vec{a}\times\vec{b}\,\right)\right]\right|=\left|\left(\vec{a}\times\vec{b}\,\right)\cdot\left(\vec{a}\times\vec{b}\,\right)\right|=\left|\vec{a}\times\vec{b}\,\right|^2=|\vec{a}\,|^2|\vec{b}\,|^2\,\mathrm{sen}^2(\theta)](/wiki/images/math/9/1/4/91424d288cf94f5e468a1d5771688c26.png)
donde se ha tenido en cuenta que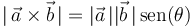 
.
