No Boletín - Cálculo de la altura de un paralelepípedo (Ex.Jun/13)
De Laplace
1 Enunciado
Sea el paralelepípedo que tiene como aristas a los tres vectores siguientes:
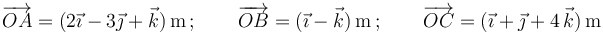
¿Cuánto mide la altura de este paralelepípedo si se considera que su base es la cara que tiene como lados a
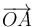y 
?
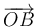2 Solución
El volumen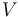 
de un paralelepípedo se calcula como el valor absoluto del producto mixto de los tres vectores que definen sus aristas:
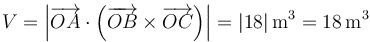
Por otra parte, si la base del paralelepípedo es la cara que tiene como lados a
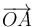y 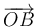, se sabe que el área 
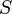de dicho paralelogramo viene dada por el módulo del producto vectorial de esos dos vectores:
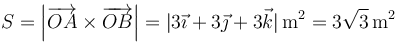
Finalmente, calculamos la altura 
del paralelepípedo como el cociente entre su volumen 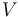y el área 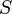de su base:
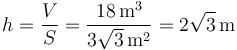
Veamos ahora un procedimiento alternativo para hallar la altura. Se calcula un vector 
normal a la base del paralelepípedo, y dividiéndolo por su módulo (normalización) se obtiene un vector unitario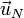 
en su misma dirección:
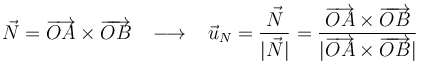
A continuación, se observa por inspección geométrica que la altura del paralelepípedo coincide con el valor absoluto de la proyección del vector-arista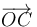 
sobre la dirección normal a la base. Así que dicha altura se puede calcular como el valor absoluto del producto escalar del vector 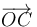por el vector unitario :
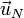![h=\left|\mathrm{proy}_{\parallel\vec{N}}\left[\overrightarrow{OC}\right]\right|=\left|\overrightarrow{OC}\cdot\vec{u}_N\right|=\left|\overrightarrow{OC}\cdot\frac{\overrightarrow{OA}\times\overrightarrow{OB}}{|\overrightarrow{OA}\times\overrightarrow{OB}|}\right|=\frac{|\overrightarrow{OC}\cdot(\overrightarrow{OA}\times\overrightarrow{OB})|}{|\overrightarrow{OA}\times\overrightarrow{OB}|}=\frac{|\overrightarrow{OA}\cdot(\overrightarrow{OB}\times\overrightarrow{OC})|}{|\overrightarrow{OA}\times\overrightarrow{OB}|}=\frac{V}{S}](/wiki/images/math/b/e/d/beda8030acef7c72d582114086cf7ed2.png)
expresión que, como puede comprobarse, es equivalente (por permutabilidad cíclica del producto mixto) a la del procedimiento anterior.
