Problemas de cinemática del punto material (G.I.T.I.)
De Laplace
1 Ejemplo de movimiento plano en 3D
Una partícula describe un movimiento según la ecuación horaria
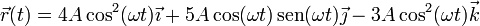
- Calcule la velocidad y la aceleración instantáneas de este movimiento.
- Determine el parámetro arco como función del tiempo y escriba la ecuación de la trayectoria como función del parámetro arco.
- Calcule el triedro de Frenet asociado a la trayectoria en cada instante, así como las componentes intrínsecas de la aceleración.
- Halle el radio de curvatura y la posición del centro de curvatura en cada instante. ¿Qué tipo de movimiento describe la partícula?
2 Evolvente de una circunferencia
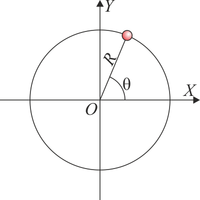
La evolvente de una circunferencia es la curva plana que se obtiene cuando se desenrolla un hilo tenso de un carrete circular. Suponga que se tiene una bobina de radio A que se va desenrollando a ritmo constante, de forma que el punto C donde el hilo deja de hacer contacto con el carrete forma un ángulo θ = ωt con el eje OX. Una partícula material se encuentra en el punto P situado en el extremo del hilo, moviéndose con este extremo a medida que el hilo se va desenrollando.
- Determine el vector de posición de la partícula.
- Calcule la velocidad y la aceleración de la partícula.
- Determine la ley horaria s = s(t).
- Halle los vectores tangente y normal a la trayectoria.
- Halle el radio de curvatura y el centro de curvatura.
3 Movimiento de partícula sujeta de un hilo
Una barra rígida AB de longitud L se mueve en un plano vertical OXY, manteniendo su extremo A articulado en un punto del eje horizontal de coordenadas 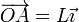 , y verificando la ley horaria θ(t) = 2ωt, con
, y verificando la ley horaria θ(t) = 2ωt, con 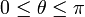 y siendo ω = cte. Un hilo inextensible de longitud 2L tiene uno de sus extremos conectado al origen del sistema de referencia (punto O), mientras que del otro cuelga una partícula P que mantiene al hilo siempre tenso. El hilo se apoya sobre una pequeña polea de radio despreciable situada en el extremo B de la barra, de forma que el tramo
y siendo ω = cte. Un hilo inextensible de longitud 2L tiene uno de sus extremos conectado al origen del sistema de referencia (punto O), mientras que del otro cuelga una partícula P que mantiene al hilo siempre tenso. El hilo se apoya sobre una pequeña polea de radio despreciable situada en el extremo B de la barra, de forma que el tramo 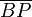 permanece siempre paralelo al eje OY (ver figura). Se pide:
permanece siempre paralelo al eje OY (ver figura). Se pide:
- Ecuaciones horarias del punto P,
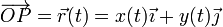 .
.
- Instante del tiempo tM en que la partícula alcanza su altura máxima.
- Radio de curvatura de la trayectoria seguida por P, en el instante considerado en el apartado anterior.
4 Ejemplo de movimiento rectilíneo
Una partícula efectúa un movimiento rectilíneo tal que si x(t) es la posición a lo largo de la recta y vx(t) la componente de la velocidad en dicha dirección, se cumple en todo instante

- Determine la aceleración en cada punto. ¿Qué tipo de movimiento efectúa la partícula?
- Si en t = 0 la partícula se encuentra en x = x0, ¿cuál es su posición en cualquier instante posterior?
5 Rectilíneo con desaceleración creciente (Ex.Nov/11)
Una partícula está recorriendo el eje OX en sentido positivo con una celeridad constante de 25 m/s. En un instante dado (t=0) se detecta un obstáculo en su trayectoria a 50 m por delante de ella. A partir de dicho instante se le aplica a la partícula una desaceleración creciente en el tiempo según la fórmula 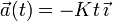 , donde
, donde 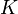 es una constante de valor igual a 8.00 m/s3. ¿Cuánto tiempo tardará en detenerse la partícula? ¿A qué distancia del obstáculo se detendrá?
es una constante de valor igual a 8.00 m/s3. ¿Cuánto tiempo tardará en detenerse la partícula? ¿A qué distancia del obstáculo se detendrá?
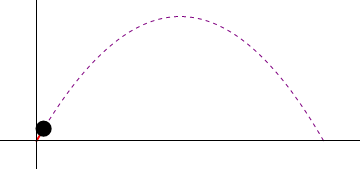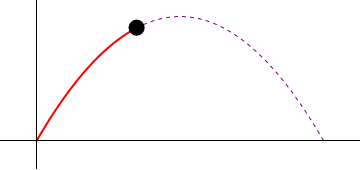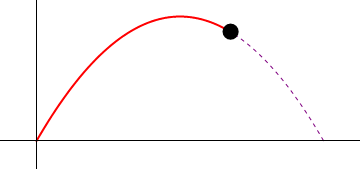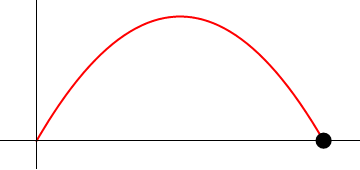
6 Tiro parabólico
Supóngase el movimiento de un proyectil que se caracteriza por poseer una aceleración constante

una posición inicial nula (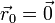 ) y una velocidad inicial que forma un ángulo α con la horizontal y tiene rapidez inicial v0.
) y una velocidad inicial que forma un ángulo α con la horizontal y tiene rapidez inicial v0.
- Determine el vector de posición, la velocidad y la aceleración en cada instante.
- Calcule la celeridad y el vector tangente en el instante en el cual el proyectil se encuentra a máxima altura.
- Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal, en el mismo instante del apartado anterior.
- Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria.
7 Movimiento circular en torno a un eje oblicuo
Una partícula gira alrededor de un eje que pasa por el origen de coordenadas y está orientado según la dirección y el sentido del vector 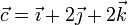 . La aceleración angular de este movimiento es constante y de módulo 1 rad/s². La velocidad angular inicial es nula. Si en
. La aceleración angular de este movimiento es constante y de módulo 1 rad/s². La velocidad angular inicial es nula. Si en  la partícula se encuentra en
la partícula se encuentra en 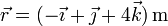 calcule, para este instante
calcule, para este instante
- La velocidad y la aceleración.
- Las componentes intrínsecas de la aceleración.
8 Ejemplo de movimiento helicoidal
Una partícula se mueve a lo largo de la hélice descrita por la ecuación paramétrica
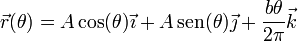
donde A y b son constantes conocidas. El movimiento de la partícula sigue la ley horaria
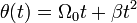
donde Ω0 y β son constantes conocidas.
- Determine el parámetro arco de la hélice descrita, como función del parámetro θ y del tiempo.
- Halle la rapidez del movimiento.
- Calcule la componente tangencial de la aceleración de la partícula en todo instante.
- Para el instante t = 0 calcule la velocidad y la aceleración de la partícula.
- Para el mismo instante, halle los vectores del triedro de Frenet, así como el radio de curvatura de la partícula y su aceleración normal.
9 Movimiento descrito en coordenadas polares
En un plano descrito mediante coordenadas polares, se mueve una partícula conforme a las ecuaciones horarias
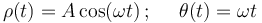
donde A y ω son constantes conocidas.
- Calcule la rapidez del movimiento.
- Halle el vector aceleración y sus componentes intrínsecas.
- Determine los vectores tangente y normal a la trayectoria en cada instante.
- Calcule el radio de curvatura.
10 Movimiento en espiral descrito en polares (Ex.Nov/11)
Una partícula recorre una espiral logarítmica, estando su posición en cada instante de tiempo descrita en coordenadas polares mediante las ecuaciones horarias:
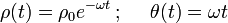
donde 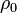 y
y 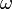 son constantes conocidas.
son constantes conocidas.
- Calcule el vector velocidad y la rapidez del movimiento.
- Halle el vector aceleración y sus componentes intrínsecas.
- Calcule el radio de curvatura.
11 No Boletín - Aceleración a partir de ley horaria y radio de curvatura (Ex.Oct/14)
Una partícula recorre cierta curva parametrizada naturalmente, conociéndose la ley horaria y el valor del radio de curvatura (que es constante):
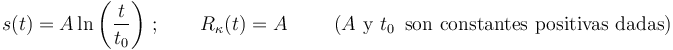
- ¿Cuánto vale el módulo de su aceleración?
- Los datos conocidos permiten saber con certeza que este movimiento es... (Nota: Sólo una opción es correcta)
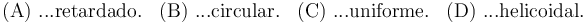
12 No Boletín - Adelantamiento entre vehículos (Ex.Nov/11)
Dos vehículos (A y B) avanzan por una misma carretera con celeridades variables en el tiempo pero tales que en todo instante se cumple que 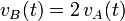 . El vehículo lento (A) va inicialmente por delante porque partió de un punto más adelantado. En cierto instante, y justo en una curva, el vehículo rápido (B) da alcance al lento (A). ¿Cuáles son las relaciones entre las respectivas aceleraciones tangenciales y entre las respectivas aceleraciones normales de ambos vehículos en el preciso instante del adelantamiento? ¿Son dichas relaciones necesariamente ciertas también para todo instante anterior o posterior al adelantamiento?
. El vehículo lento (A) va inicialmente por delante porque partió de un punto más adelantado. En cierto instante, y justo en una curva, el vehículo rápido (B) da alcance al lento (A). ¿Cuáles son las relaciones entre las respectivas aceleraciones tangenciales y entre las respectivas aceleraciones normales de ambos vehículos en el preciso instante del adelantamiento? ¿Son dichas relaciones necesariamente ciertas también para todo instante anterior o posterior al adelantamiento?
13 No Boletín - Anilla ensartada en dos varillas (Ex.Nov/10)
Una pequeña anilla P se encuentra ensartada en la intersección de dos barras giratorias. Los extremos fijos de las barras distan una cantidad L y giran en el mismo sentido con la misma velocidad angular de módulo constante Ω de forma que describen los ángulos indicados en la figura:
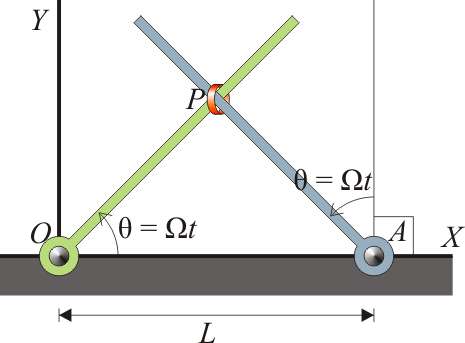
- ¿Cuáles son las ecuaciones horarias de P?
- ¿Qué clase de trayectoria describe?
- ¿Qué tipo de movimiento realiza?
14 No Boletín - Automóviles con m.r.u. y m.r.u.a. (Ex.Nov/12)
Un automóvil A recorre el eje OX con una velocidad constante 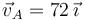 km/h, hallándose en el punto
km/h, hallándose en el punto 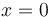 en el instante
en el instante 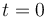 . En ese mismo instante un segundo automóvil B, que se encontraba en reposo en el punto
. En ese mismo instante un segundo automóvil B, que se encontraba en reposo en el punto 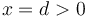 , comienza a moverse con una aceleración constante
, comienza a moverse con una aceleración constante 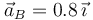 m/s2.
m/s2.
¿Cuál era la distancia 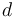 que separaba a ambos automóviles en el instante inicial si observamos que A logra alcanzar a B por un momento pero no llega a adelantarlo?
que separaba a ambos automóviles en el instante inicial si observamos que A logra alcanzar a B por un momento pero no llega a adelantarlo?
15 No Boletín - Bólido con m.c.u. (Ex.Nov/12)
La gravedad media en la superficie terrestre (g = 9.80665 m/s2) es utilizada a veces como unidad de aceleración. Sea un bólido que recorre con celeridad constante un circuito circular de diámetro igual a 1500 yardas (1 yd = 0.9144 m) y que tarda exactamente 1 minuto en completar cada vuelta. ¿Cuánto vale la aceleración (en módulo) de dicho bólido expresada en la unidad g?
16 No Boletín - Celeridad media a partir de celeridad instantánea (Ex.Nov/12)
Un punto material recorre cierta trayectoria con una celeridad que varía en el tiempo según la fórmula:

siendo 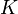 una constante de valor igual a
una constante de valor igual a 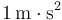
¿Cuál es la celeridad media del punto material en el intervalo de tiempo transcurrido entre 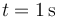 y
y 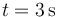 ?
?
17 No Boletín - Celeridad media a partir de ley horaria (Ex.Oct/13)
Un punto material recorre cierta trayectoria parametrizada naturalmente con la siguiente ley horaria:

siendo 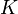 y
y 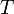 sendas constantes conocidas.
sendas constantes conocidas.
¿Cuál es la celeridad media del punto material en el intervalo de tiempo transcurrido entre 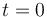 y
y 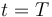 ?
?
18 No Boletín - Celeridad media a partir de ley horaria II (Ex.Oct/15)
Una partícula realiza un movimiento armónico simple con la siguiente ecuación horaria:
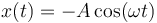
donde la amplitud 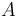 y la pulsación
y la pulsación 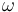 son constantes conocidas.
son constantes conocidas.
¿Cuál es la celeridad media de la partícula en el intervalo de tiempo transcurrido entre 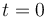 y
y 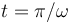 ?
?
19 No Boletín - Celeridad media de un vehículo (Ex.Ene/12)
Un automóvil recorre cierto trayecto del siguiente modo: la mitad de su longitud con celeridad constante de 120 km/h, y la otra mitad con celeridad constante de 60 km/h. ¿Cuál ha sido su celeridad media en el recorrido total?
20 No Boletín - Celeridad media en viaje mixto (Ex.Jun/13)
Un automóvil realiza un viaje de 100 km que consta de una primera parte sobre una carretera asfaltada y una segunda parte sobre un carril de tierra. En la carretera asfaltada avanza con una celeridad constante de 120 km/h, mientras que en el carril de tierra lo hace con una celeridad constante de 30 km/h. Sabiendo que la celeridad media en el trayecto total es de 75 km/h, ¿cuál es la longitud recorrida sobre el carril de tierra?
21 No Boletín - Celeridad, aceleración tangencial y radio de curvatura (Ex.Nov/12)
En el plano OXY, una partícula 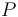 recorre la trayectoria:
recorre la trayectoria:
![\overrightarrow{OP}\equiv\vec{r}(\psi)=R\,[1+\mathrm{cos}(\psi)\,]\,\vec{\imath}\,+R\,[\psi+\mathrm{sen}(\psi)\,]\,\vec{\jmath}](/wiki/images/math/4/3/f/43f8f1e3d6682867c434ff44ecf2524d.png) (
( es una constante conocida)
es una constante conocida)siguiendo la ley horaria:
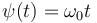 (
(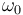 es otra constante conocida)
es otra constante conocida)Las tres preguntas siguientes se refieren al instante en el que 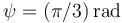 .
.
- ¿Cuál es la celeridad de la partícula en dicho instante?
- ¿Cuánto vale la componente tangencial de la aceleración en dicho instante?
- ¿Cuál es el radio de curvatura de la trayectoria en dicho instante?
22 No Boletín - Celeridad, aceleración tangencial y radio de curvatura II (Ex.Oct/14)
En el plano OXY, una partícula  se mueve conforme a la ecuación horaria:
se mueve conforme a la ecuación horaria:
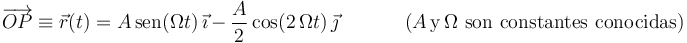
Las tres preguntas siguientes se refieren al instante 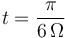 .
.
- ¿Cuál es la celeridad de la partícula en dicho instante?
- ¿Cuánto vale la componente tangencial de su aceleración en dicho instante?
- ¿Cuál es el radio de curvatura de su trayectoria en dicho instante?
23 No Boletín - Centro de curvatura y período de un circular uniforme (Ex.Oct/15)
Desde un triedro cartesiano 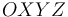 , se observa a una partícula que realiza un movimiento circular uniforme. Periódicamente, la partícula pasa por el punto
, se observa a una partícula que realiza un movimiento circular uniforme. Periódicamente, la partícula pasa por el punto  (origen de coordenadas) con los siguientes valores instantáneos de velocidad y
aceleración:
(origen de coordenadas) con los siguientes valores instantáneos de velocidad y
aceleración:

- ¿Cuáles son las coordenadas del centro de curvatura de la trayectoria?
- ¿Cuál es el período del movimiento?
24 No Boletín - Componentes intrínsecas en un movimiento circular (Ex.Jun/13)
El ángulo 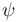 que forman entre sí los vectores velocidad y aceleración de una partícula puede determinarse a partir del cociente entre las componentes intrínsecas de su aceleración:
que forman entre sí los vectores velocidad y aceleración de una partícula puede determinarse a partir del cociente entre las componentes intrínsecas de su aceleración:
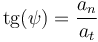
Sea una partícula  que recorre la circunferencia de radio
que recorre la circunferencia de radio  :
:
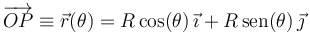
¿Para cuál de las siguientes leyes horarias se mantiene constante a lo largo del tiempo el ángulo 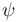 formado por la velocidad y la aceleración de la partícula? (Nota:
formado por la velocidad y la aceleración de la partícula? (Nota: 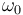 ,
, 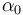 y
y  son constantes positivas conocidas.)
son constantes positivas conocidas.)
1) 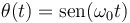
2) 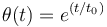
3) 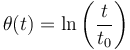
4) 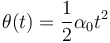
25 No Boletín - Cuestión sobre componentes intrínsecas de la aceleración (Ex.Nov/16)
Una partícula, cuya celeridad inicial es 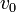 , recorre una hélice de radio de curvatura
, recorre una hélice de radio de curvatura 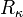 parametrizada naturalmente, de tal modo que se cumple la condición de que la suma de sus aceleraciones tangencial y normal es
nula en todo instante de tiempo:
parametrizada naturalmente, de tal modo que se cumple la condición de que la suma de sus aceleraciones tangencial y normal es
nula en todo instante de tiempo:
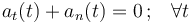
¿Para cuál de las siguientes leyes horarias se cumple dicha condición?
- (1)
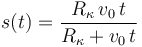
- (2)
![s(t)=R_{\kappa}\,[\,e^{(v_0t/R_{\kappa})}-1\,]\,](/wiki/images/math/6/5/6/6562f73cd5a42f6361f6886489ed12e9.png)
- (3)
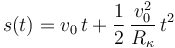
- (4)
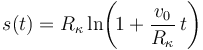
26 No Boletín - Cuestión sobre movimiento de aceleración constante (Ex.Oct/14)
Si una partícula se mueve de tal modo que su aceleración es un vector constante en el tiempo, ¿cuál de las siguientes afirmaciones es necesariamente cierta? (NOTA: sólo una de las cuatro opciones es correcta).
1) La celeridad de la partícula varía linealmente con el tiempo.
2) La partícula realiza un movimiento rectilíneo uniformemente acelerado.
3) Es imposible que la partícula alcance un reposo instantáneo.
4) La trayectoria de la partícula es plana, aunque puede no ser recta.
27 No Boletín - Cuestión sobre radio de curvatura (Ex.Oct/15)
Una partícula, que se hallaba en reposo en el instante inicial (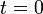 ), se mueve de tal modo que su aceleración tangencial y su aceleración normal son ambas constantes no nulas:
), se mueve de tal modo que su aceleración tangencial y su aceleración normal son ambas constantes no nulas:

¿Cómo evoluciona el radio de curvatura de la trayectoria de esta partícula? (NOTA: sólo una de las cuatro opciones es correcta).
- (a) Es constante.
- (b) Aumenta linealmente con el tiempo.
- (c) Aumenta cuadráticamente con el tiempo.
- (d) Aumenta cúbicamente con el tiempo.
28 No Boletín - Cuestión sobre velocidad y aceleración en el triedro de Frenet (Ex.Oct/13)
Para un instante dado, se representan la velocidad  y la aceleración
y la aceleración 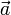 de una partícula en sus orientaciones relativas a algún plano del triedro de Frenet
de una partícula en sus orientaciones relativas a algún plano del triedro de Frenet 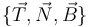 . (Nota: se utiliza
. (Nota: se utiliza  para vectores perpendiculares al plano del papel y de sentido saliente, y
para vectores perpendiculares al plano del papel y de sentido saliente, y  para vectores perpendiculares al plano del papel y de sentido entrante).
para vectores perpendiculares al plano del papel y de sentido entrante).
¿Cuál es el diagrama correcto si se sabe que el movimiento es uniforme no rectilíneo?
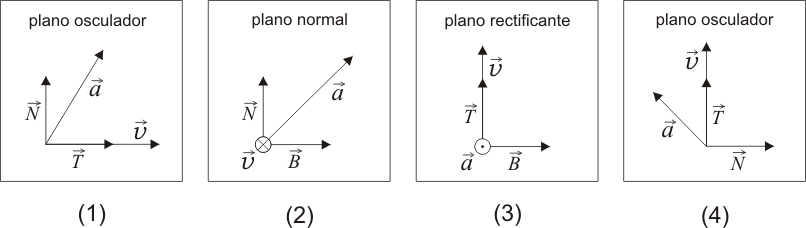
29 No Boletín - Descripción vectorial de un movimiento circular (Ex.Nov/16)
Desde un triedro cartesiano 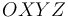 , se observa el movimiento circular de una partícula
, se observa el movimiento circular de una partícula  cuyo eje de giro pasa
por el origen de coordenadas
cuyo eje de giro pasa
por el origen de coordenadas  . En cierto instante, los vectores de posición, velocidad angular y aceleración angular de
. En cierto instante, los vectores de posición, velocidad angular y aceleración angular de  valen:
valen:
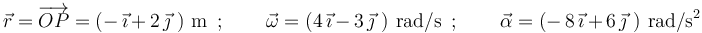
- ¿Cuánto vale la aceleración de la partícula en dicho instante?
- ¿Cuál es el radio de curvatura de su trayectoria?
30 No Boletín - Dos móviles sobre el eje OX acercándose (Ex.Oct/14)
Un móvil A recorre el eje OX con una velocidad constante 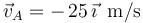 , hallándose en el punto
, hallándose en el punto 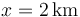 en el instante inicial
en el instante inicial 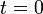 . En ese mismo instante un segundo móvil B, que se encuentra en reposo en el punto
. En ese mismo instante un segundo móvil B, que se encuentra en reposo en el punto 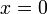 , comienza a moverse con una aceleración creciente en el tiempo según la fórmula:
, comienza a moverse con una aceleración creciente en el tiempo según la fórmula:
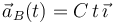
donde  es una constante de valor igual a
es una constante de valor igual a 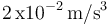 .
.
- ¿Cuánto tiempo transcurre hasta el instante en el que la celeridad de B alcanza el mismo valor que la celeridad de A?
- ¿Qué distancia hay entre los móviles A y B en el instante al que se refiere la pregunta anterior?
31 No Boletín - Ejemplo de movimiento circular no uniforme (Ex.Sep/11)
Una partícula de masa m describe un movimiento circular de radio R, tal que su velocidad angular instantánea cumple

con k una constante y θ el ángulo que el vector de posición instantánea forma con el eje OX.
- Determine la aceleración angular de la partícula como función del ángulo θ.
- Halle las componentes intrínsecas de la aceleración lineal.
32 No Boletín - Identificación de movimiento (Ex.Nov/10)
Una partícula se mueve según las ecuaciones horarias

- ¿Qué trayectoria sigue la partícula?
- Determine la ley horaria s(t). Suponga que s(0) = 0.
- ¿Qué tipo de movimiento describe la partícula?
33 No Boletín - Identificación de movimiento II (Ex.Nov/11)
Un punto material se mueve con ecuación horaria:
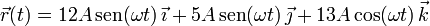
donde  y
y 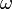 son constantes conocidas.
son constantes conocidas.
- Determine la ley horaria s(t) suponiendo que s(0) = 0.
- Determine el triedro de Frenet y el radio de curvatura en cada instante.
- Identifique el tipo de movimiento.
34 No Boletín - Identificación de movimiento III (Ex.Oct/13)
En el triedro cartesiano 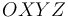 , una partícula
, una partícula  se mueve conforme a la ecuación horaria:
se mueve conforme a la ecuación horaria:
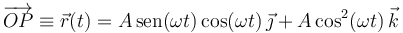
donde  y
y 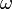 son constantes conocidas.
son constantes conocidas.
- ¿Qué trayectoria sigue la partícula?
- ¿Con qué tipo de movimiento es recorrida dicha trayectoria?
35 No Boletín - Movimiento circular con celeridad variable en el tiempo (Ex.Dic/12)
Una partícula realiza un movimiento circular con celeridad variable en el tiempo conforme a la ley:
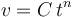
donde  es una constante de valor igual a
es una constante de valor igual a 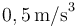 .
.
- ¿Cuál es el valor del exponente
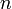 ?
?
- ¿Cómo varía durante este movimiento el cociente entre la aceleración normal y la aceleración tangencial de la partícula?
36 No Boletín - Movimiento en espiral descrito en polares II (Ex.Oct/15)
Una partícula recorre una espiral de Arquímedes, estando su posición en cada instante de tiempo descrita en coordenadas polares mediante las ecuaciones horarias:
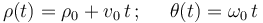
donde 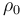 ,
, 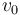 y
y 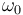 son constantes positivas conocidas.
son constantes positivas conocidas.
- Determine la aceleración de la partícula expresada en la base polar.
- Calcule la aceleración tangencial de la partícula.
37 No Boletín - Otro movimiento de partícula sujeta de un hilo (Ex.Sep/12)
La barra rígida 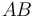 , de longitud
, de longitud  , se halla contenida en el plano vertical
, se halla contenida en el plano vertical 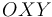 y rota alrededor de su extremo fijo
y rota alrededor de su extremo fijo  , cuya posición viene dada por
, cuya posición viene dada por 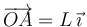 . Un hilo inextensible, de longitud
. Un hilo inextensible, de longitud 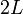 , tiene uno de sus extremos conectado a un deslizador puntual
, tiene uno de sus extremos conectado a un deslizador puntual  que puede desplazarse sobre el eje vertical
que puede desplazarse sobre el eje vertical 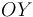 , mientras que del otro extremo cuelga una partícula P que mantiene al hilo tenso.
, mientras que del otro extremo cuelga una partícula P que mantiene al hilo tenso.
El hilo se apoya sobre una pequeña polea de radio despreciable situada en el extremo B de la barra, y el movimiento del mecanismo es tal que el tramo 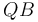 permanece siempre paralelo al eje
permanece siempre paralelo al eje  , y el tramo
, y el tramo 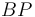 permanece siempre paralelo al eje
permanece siempre paralelo al eje 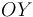 (ver figura).
(ver figura).
- Determine el vector de posición de la partícula en función del ángulo que forma la barra
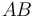 con el eje
con el eje  , es decir,
, es decir, 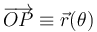 .
.
- Para la ley horaria
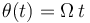 (donde
(donde 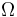 es una constante positiva conocida, y
es una constante positiva conocida, y 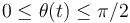 ), halle los vectores velocidad y aceleración de la partícula P en función del tiempo.
), halle los vectores velocidad y aceleración de la partícula P en función del tiempo.
- Sólo para el instante en que
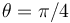 , determine las componentes intrínsecas de la aceleración y el radio de curvatura de la partícula P.
, determine las componentes intrínsecas de la aceleración y el radio de curvatura de la partícula P.
38 No Boletín - Otro tiro parabólico (Ex.Sep/15)
Un proyectil se mueve en el plano vertical 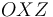 . Se conoce su aceleración constante (debida a su propio peso), y también su posición y su velocidad en el instante inicial (
. Se conoce su aceleración constante (debida a su propio peso), y también su posición y su velocidad en el instante inicial (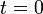 ):
):
![\vec{a}(t)=-g\,\vec{k}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\vec{r}(0)=h\,\vec{k}\,\,\,;
\,\,\,\,\,\,\,\,\,\,\,\,\vec{v}(0)=v_0\,[\,\mathrm{cos}(\theta)\,\vec{\imath}+
\mathrm{sen}(\theta)\,\vec{k}\,]](/wiki/images/math/d/e/9/de9c3ce06bffd9ab7a69070c76c7c6b8.png)
donde  ,
,  y
y 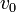 tienen valores positivos, y
tienen valores positivos, y  está comprendido en el intervalo
está comprendido en el intervalo 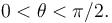
- Determine el radio de curvatura de la trayectoria del proyectil en el instante inicial.
- Determine la celeridad del proyectil en el instante en el que su trayectoria corta al eje
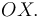
39 No Boletín - Otro tiro parabólico II (proyectil y ave) (Ex.Nov/16)
Un proyectil y un ave se mueven simultáneamente en el plano vertical 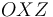 . El proyectil tiene una aceleración constante (de módulo
. El proyectil tiene una aceleración constante (de módulo  ) debida a la gravedad, y su posición y su velocidad iniciales son las correspondientes a un lanzamiento desde el
origen de coordenadas con celeridad inicial
) debida a la gravedad, y su posición y su velocidad iniciales son las correspondientes a un lanzamiento desde el
origen de coordenadas con celeridad inicial 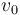 y con un ángulo
y con un ángulo 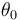 sobre el eje horizontal
sobre el eje horizontal  (siendo
(siendo 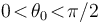 ):
):
![\vec{a}(t)=-\,g\,\vec{k}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\vec{r}\,(0)=\vec{0}\,\,\,;
\,\,\,\,\,\,\,\,\,\,\,\,\vec{v}\,(0)=v_{0}\,[\,\mathrm{cos}(\theta_0)\,\vec{\imath}+
\mathrm{sen}(\theta_0)\,\vec{k}\,]](/wiki/images/math/b/f/b/bfbc1212e30dc0f75be9e1c4f279a2f1.png)
Por otra parte, el ave vuela con celeridad constante 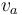 y manteniendo una altura constante
y manteniendo una altura constante  , y su posición inicial está en la vertical del punto de lanzamiento del proyectil, es decir:
, y su posición inicial está en la vertical del punto de lanzamiento del proyectil, es decir:

Considerando que  ,
, 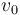 y
y  tienen valores positivos conocidos, y sabiendo que el ave recibe el impacto del proyectil justo en el instante en el que éste alcanza la posición de máxima altura en su trayectoria parabólica, determine (en función de
tienen valores positivos conocidos, y sabiendo que el ave recibe el impacto del proyectil justo en el instante en el que éste alcanza la posición de máxima altura en su trayectoria parabólica, determine (en función de  ,
, 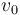 y
y  ):
):
- El ángulo
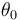 de lanzamiento del proyectil.
de lanzamiento del proyectil.
- La celeridad constante
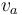 del ave.
del ave.
40 No Boletín - Rectilíneo con aceleración creciente (Ex.Oct/13)
Una partícula, inicialmente en reposo en el origen de coordenadas, se mueve con una aceleración creciente en el tiempo según la fórmula:
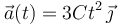
siendo  una constante de valor igual a
una constante de valor igual a 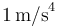 .
¿A qué distancia del origen de coordenadas se hallará la partícula en el instante
.
¿A qué distancia del origen de coordenadas se hallará la partícula en el instante 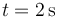 ?
?
41 No Boletín - Rectilíneo con aceleración exponencialmente decreciente (Ex.Oct/15)
Una partícula, que se hallaba en reposo en el instante inicial (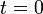 ), se mueve con una aceleración exponencialmente
decreciente en el tiempo según la fórmula:
), se mueve con una aceleración exponencialmente
decreciente en el tiempo según la fórmula:
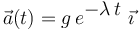
donde 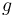 y
y 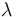 son constantes positivas conocidas.
son constantes positivas conocidas.
¿Hacia qué valor límite tiende la velocidad de dicha partícula cuando se deja pasar mucho tiempo (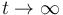 ) ?
) ?
42 No Boletín - Rotación y traslación terrestres
La Tierra rota uniformemente con respecto a su eje con velocidad angular ω constante. Encuentre en función de la latitud λ, la velocidad y la aceleración de un punto sobre la superficie terrestre, debidas a dicha rotación (radio de la Tierra: 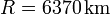 )
)
Compare los módulos de los valores anteriores para el caso de un punto en el Ecuador, con los correspondientes al movimiento de traslación alrededor del Sol (distancia Tierra-Sol aproximadamente constante e igual a 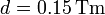 ).
).
43 No Boletín - Tipo de movimiento rectilíneo (Ex.Nov/16)
Una partícula se mueve a lo largo del eje  y, por tanto, sus vectores de posición, velocidad y aceleración vienen dados,
respectivamente, por las expresiones
y, por tanto, sus vectores de posición, velocidad y aceleración vienen dados,
respectivamente, por las expresiones 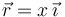 ,
, 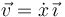 y
y 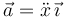 .
.
Se sabe que en todo instante de tiempo se verifica la siguiente relación entre su velocidad y su posición:
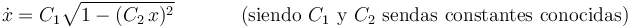
Determine su aceleración para poder elegir la respuesta correcta a la pregunta que se plantea a continuación.
¿Qué tipo de movimiento rectilíneo realiza esta partícula?
- (a) Uniforme.
- (b) Armónico simple.
- (c) Uniformemente acelerado.
- (d) Ninguno de los otros tres.
44 No Boletín - Valores instantáneos de velocidad y aceleración (Ex.Oct/13)
En un instante dado, la velocidad y la aceleración de una partícula son las siguientes:
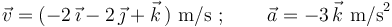
- ¿Cuánto vale en ese instante su aceleración tangencial?
- ¿Cuál es el radio de curvatura de la trayectoria en ese instante?