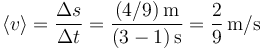No Boletín - Celeridad media a partir de celeridad instantánea (Ex.Nov/12)

De Laplace

1 Enunciado

Un punto material recorre cierta trayectoria con una celeridad que varía en el tiempo según la fórmula:

$v(t)=\frac{K}{t^3}\;\;\;\;\; \mathrm{(para}\,\,t>0\mathrm{)}$

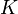siendo $K\,$ una constante de valor igual a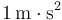 $1 \,\mathrm{m}\cdot\mathrm{s}^2\,$

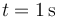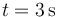¿Cuál es la celeridad media del punto material en el intervalo de tiempo transcurrido entre $t=1\,\mathrm{s}\,$ y $t=3\,\mathrm{s}\,$ ?

2 Solución

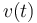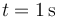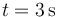La celeridad instantánea $v(t)\,$ nos proporciona la derivada del parámetro arco respecto al tiempo en cada instante. Por tanto, mediante su integración podemos obtener la longitud de trayectoria recorrida por el punto material durante el intervalo de tiempo transcurrido entre $t=1\,\mathrm{s}\,$ y $t=3\,\mathrm{s}\,$ (es decir, el incremento del parámetro arco durante dicho intervalo):

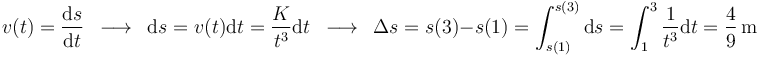
$v(t)=\frac{\mathrm{d}s}{\mathrm{d}t}\,\,\,\longrightarrow\,\,\,\mathrm{d}s=v(t)\mathrm{d}t=\frac{K}{t^3}\mathrm{d}t\,\,\,\longrightarrow\,\,\,\Delta s=s(3)-s(1)=\int_{s(1)}^{s(3)}\mathrm{d}s=\int_{1}^{3}\frac{1}{t^3}\mathrm{d}t=\frac{4}{9}\,\mathrm{m}$

La celeridad media del punto material en dicho intervalo de tiempo viene dada por el siguiente cociente:

$\left\langle v\right\rangle = \frac{\Delta s}{\Delta t}=\frac{(4/9)\,\mathrm{m}}{(3-1)\,\mathrm{s}}=\frac{2}{9}\,\mathrm{m/s}$

No Boletín - Celeridad media a partir de celeridad instantánea (Ex.Nov/12)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES