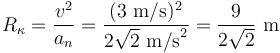No Boletín - Valores instantáneos de velocidad y aceleración (Ex.Oct/13)
De Laplace
1 Enunciado
En un instante dado, la velocidad y la aceleración de una partícula son las siguientes:
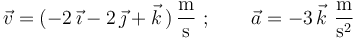
- ¿Cuánto vale en ese instante su aceleración tangencial?
- ¿Cuál es el radio de curvatura de la trayectoria en ese instante?
2 Aceleración tangencial
Calculamos en primer lugar la celeridad instantánea (módulo del vector velocidad):
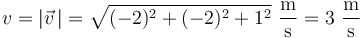
y el módulo del vector aceleración instantánea:
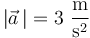
La aceleración tangencial en el instante de interés puede calcularse a partir de la velocidad y la aceleración mediante la fórmula:
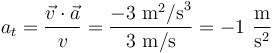
NOTA: La aceleración tangencial también puede calcularse como derivada temporal de la celeridad, pero para ello necesitaríamos conocer la celeridad como función del tiempo. Nótese que la celeridad que conocemos en este ejercicio es la celeridad en un instante concreto. Por eso, sería un disparate tratar de calcular la aceleración tangencial derivando respecto al tiempo esa "celeridad constante", ya que no se trata en realidad de una "función constante" sino del valor que toma una función (que desconocemos) en un instante concreto.
3 Radio de curvatura
Calculamos ahora la aceleración normal de la partícula en el instante de interés a partir de la aceleración tangencial y del módulo del vector aceleración:
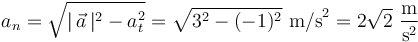
Nótese que dicha aceleración normal también puede calcularse a partir de la velocidad y la aceleración mediante la fórmula:
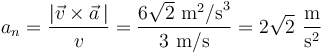
Finalmente, a partir de la aceleración normal y la celeridad, obtenemos el valor del radio de curvatura de la trayectoria en el instante analizado: