2.7. Movimiento circular en torno a un eje oblicuo
De Laplace
Contenido |
1 Enunciado
Una partícula gira alrededor de un eje que pasa por el origen de coordenadas y está orientado según la dirección y el sentido del vector 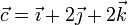 . La aceleración angular de este movimiento es constante y de módulo 1 rad/s². La velocidad angular
inicial es nula. Si en
. La aceleración angular de este movimiento es constante y de módulo 1 rad/s². La velocidad angular
inicial es nula. Si en  la partícula se encuentra en
la partícula se encuentra en 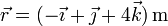 calcule, para este instante
calcule, para este instante
- La velocidad y la aceleración.
- Las componentes intrínsecas de la aceleración.
2 Velocidad y aceleración
2.1 Velocidad
La velocidad de una partícula que describe un movimiento circular en torno a un eje puede escribirse en la forma
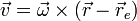
siendo 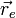 un punto del eje de giro (no necesariamente el centro de la circunferencia). De acuerdo con el enunciado, podemos tomar este punto como el origen de coordenadas
un punto del eje de giro (no necesariamente el centro de la circunferencia). De acuerdo con el enunciado, podemos tomar este punto como el origen de coordenadas
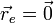
La velocidad angular la hallamos sabiendo que la aceleración angular es constante (se trata de un movimiento uniformemente acelerado)
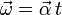
La aceleración angular (suponiendo que su sentido es el mismo que el del vector 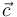 ) es
) es
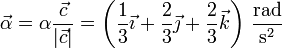
por lo que en  la velocidad angular vale
la velocidad angular vale
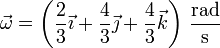
Multiplicando vectorialmente por el vector de posición obtenemos la velocidad

2.2 Aceleración
La aceleración en un movimiento circular se compone de un término asociado a la velocidad angular y otro a la aceleración angular.
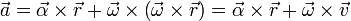
Calculándolos por separado, tenemos, para el primer término
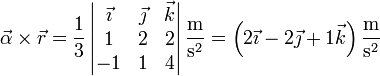
y para el segundo
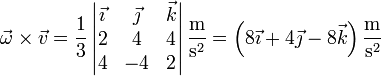
Sumando las dos contribuciones
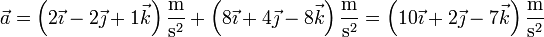
3 Componentes de la aceleración
La aceleración de la partícula se compone de dos sumandos. Uno es claramente perpendicular a la velocidad, mientras que el otro es paralelo a ella, por ser la velocidad y la aceleración angular vectores paralelos. Por tanto, tenemos
3.1 Aceleración tangencial
El vector aceleración tangencial corresponde al término
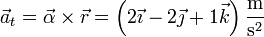
siendo la componente tangencial de la aceleración
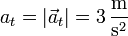
NOTA: Calcular at como el módulo de 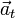 sólo se puede hacer cuando se tiene certeza de que la aceleración tangencial es positiva (movimiento acelerado), lo cual ocurre en este caso dado que los vectores
sólo se puede hacer cuando se tiene certeza de que la aceleración tangencial es positiva (movimiento acelerado), lo cual ocurre en este caso dado que los vectores 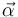 y
y  tienen el mismo sentido. En caso de duda sobre el signo de at, ésta tendrá que calcularse como el producto escalar de
tienen el mismo sentido. En caso de duda sobre el signo de at, ésta tendrá que calcularse como el producto escalar de  (o bien
(o bien 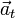 ) por el vector unitario tangente
) por el vector unitario tangente 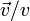 .
.
3.2 Aceleración normal
El vector aceleración normal lo da el término perpendicular a la velocidad

siendo su módulo