2.9. Movimiento descrito en coordenadas polares

De Laplace

Contenido

1 Enunciado
2 Rapidez del movimiento
3 Vector aceleración y sus componentes intrínsecas
4 Vectores tangente y normal a la trayectoria
5 Radio de curvatura

1 Enunciado

En un plano descrito mediante coordenadas polares, se mueve una partícula conforme a las ecuaciones horarias

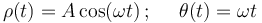
$\rho(t)=A\cos(\omega t)\,;\,\,\,\,\,\,\,\,\theta(t)=\omega t\,$

donde $A$ y $ω$ son constantes conocidas.

Calcule la rapidez del movimiento.
Halle el vector aceleración y sus componentes intrínsecas.
Determine los vectores tangente y normal a la trayectoria en cada instante.
Calcule el radio de curvatura.

2 Rapidez del movimiento

La velocidad en componentes polares viene dada por la expresión

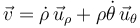
$\vec{v} = \dot{\rho}\,\vec{u}_{\rho}+\rho\dot{\theta}\,\vec{u}_{\theta}$

Calculamos, por tanto, las primeras derivadas respecto al tiempo de las ecuaciones horarias

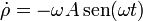
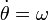
$\dot{\rho}=-\omega A\,\mathrm{sen}(\omega t)$ $\dot{\theta}=\omega$

y sustituimos

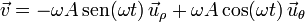
$\vec{v} = -\omega A\,\mathrm{sen}(\omega t)\,\vec{u}_{\rho}+\omega A\cos(\omega t)\,\vec{u}_{\theta}$

Finalmente, tomando módulo del vector velocidad obtenemos la rapidez del movimiento

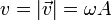
$v = |\vec{v}|=\omega A$

Se observa que hemos obtenido una rapidez constante (independiente del tiempo). Por tanto, estamos ante un movimiento uniforme.

3 Vector aceleración y sus componentes intrínsecas

La aceleración en componentes polares viene dada por la expresión

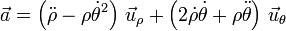
$\vec{a} = \left(\ddot{\rho}-\rho{\dot{\theta}}^2\right)\,\vec{u}_{\rho}+\left(2\dot{\rho}\dot{\theta}+\rho\ddot{\theta}\right)\,\vec{u}_{\theta}$

Necesitamos también, por tanto, las segundas derivadas respecto al tiempo de las ecuaciones horarias

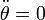
$\ddot{\rho}=-\omega^{2}\! A\cos(\omega t)$ $\ddot{\theta}=0$

y sustituyendo y operando

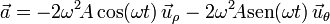
$\vec{a} = -2\omega^{2}\! A\cos(\omega t)\,\vec{u}_{\rho}-2\omega^{2}\! A\mathrm{sen}(\omega t)\,\vec{u}_{\theta}$

Para calcular la componente tangencial de la aceleración podríamos proyectar el vector aceleración sobre la dirección del vector velocidad (dirección tangente a la trayectoria), pero optaremos por una deducción más inmediata y que nos va a evitar operaciones. Sabemos que la aceleración tangencial es la derivada respecto al tiempo de la rapidez, y la rapidez ha sido previamente calculada resultando ser constante. En consecuencia

$a_t=\dot{v}=0$

Se deduce, pues, que en este caso el vector aceleración tiene dirección normal y, en consecuencia, su módulo coincide con la componente normal de la aceleración

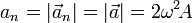
$\vec{a}_n=\vec{a}$ $a_n=|\vec{a}_n|=|\vec{a}|=2\omega^{2}\! A$

4 Vectores tangente y normal a la trayectoria

El vector tangente unitario se obtiene por normalización del vector velocidad

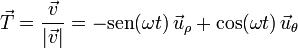
$\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\mathrm{sen}(\omega t)\,\vec{u}_{\rho}+\cos(\omega t)\,\vec{u}_{\theta}$

Al ser nula la componente tangencial de la aceleración, el vector normal principal se puede obtener por normalización del vector aceleración

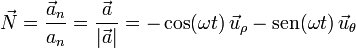
$\vec{N}=\frac{\vec{a}_n}{a_n}=\frac{\vec{a}}{|\vec{a}|}=-\cos(\omega t)\,\vec{u}_{\rho}-\mathrm{sen}(\omega t)\,\vec{u}_{\theta}$

5 Radio de curvatura

El radio de curvatura se puede calcular a partir del conocimiento de la componente normal de la aceleración y de la rapidez del movimiento

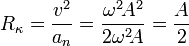
$R_{\kappa}=\frac{v^{2}}{a_n}=\frac{\omega^{2}\! A^{2}}{2\omega^{2}\! A}=\frac{A}{2}$

El hecho de que el radio de curvatura obtenido sea constante, unido a que se trata de una curva plana, nos permite saber que la trayectoria es una circunferencia. Como además vimos antes que la celeridad es constante, podemos concluir que estamos ante un movimiento circular uniforme. Si tenemos la curiosidad de ubicar el centro de la circunferencia descrita por la partícula, basta determinar la posición del centro de curvatura

$\vec{r}_c=\vec{r}+ R_{\kappa}\vec{N}$

donde $\vec{r}$ es el vector de posición de un punto genérico de la trayectoria, que en polares viene dado por

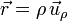
$\vec{r}=\rho\,\vec{u}_{\rho}$

Sustituyendo las expresiones ya conocidas, se obtiene

$\vec{r}_c=A\cos(\omega t)\,\vec{u}_{\rho}+\frac{A}{2}[-\mbox{cos}(\omega t)\,\vec{u}_{\rho}-\mathrm{sen}(\omega t)\,\vec{u}_{\theta}]=\frac{A}{2}[\mbox{cos}(\omega t)\,\vec{u}_{\rho}-\mathrm{sen}(\omega t)\,\vec{u}_{\theta}]$

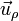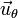La expresión obtenida puede sorprender inicialmente, ya que de una circunferencia esperábamos un centro de curvatura fijo (con vector de posición independiente del tiempo). Pero no debemos olvidar que la expresión obtenida viene dada en la base polar, cuyos vectores $\vec{u}_{\rho}$ y $\vec{u}_{\theta}$ son variables con la posición de la partícula y, por tanto, dependen también del tiempo

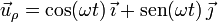
$\vec{u}_{\rho}=\mbox{cos}(\omega t)\,\vec{\imath}+\mathrm{sen}(\omega t)\,\vec{\jmath}$ $\vec{u}_{\theta}=-\mathrm{sen}(\omega t)\,\vec{\imath}+\cos(\omega t)\,\vec{\jmath}$

Recalculando la posición del centro de curvatura de la trayectoria en la base cartesiana, se obtiene

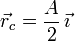
$\vec{r}_c=\frac{A}{2}\,\vec{\imath}$

Comprobamos, pues, que la circunferencia descrita por la partícula tiene su centro de curvatura en una posición fija, sobre la parte positiva del eje $O X$ y a una distancia $A / 2$ del origen de coordenadas (polo).

2.9. Movimiento descrito en coordenadas polares

De Laplace

Contenido

1 Enunciado

2 Rapidez del movimiento

3 Vector aceleración y sus componentes intrínsecas

4 Vectores tangente y normal a la trayectoria

5 Radio de curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES