No Boletín - Cuestión sobre radio de curvatura (Ex.Oct/15)
De Laplace
1 Enunciado
Una partícula, que se hallaba en reposo en el instante inicial (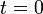 ), se mueve de tal modo que su aceleración tangencial y su aceleración normal son ambas constantes no nulas:
), se mueve de tal modo que su aceleración tangencial y su aceleración normal son ambas constantes no nulas:

¿Cómo evoluciona el radio de curvatura de la trayectoria de esta partícula? (NOTA: sólo una de las cuatro opciones es correcta).
- (a) Es constante.
- (b) Aumenta linealmente con el tiempo.
- (c) Aumenta cuadráticamente con el tiempo.
- (d) Aumenta cúbicamente con el tiempo.
2 Solución
La aceleración tangencial de una partícula viene dada por la derivada temporal de su celeridad. Así que, conocida la aceleración tangencial en todo instante 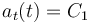 y conocida la celeridad en el instante inicial
y conocida la celeridad en el instante inicial 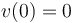 (nula por hallarse la partícula en reposo), podemos determinar la celeridad para
(nula por hallarse la partícula en reposo), podemos determinar la celeridad para 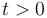 integrando la aceleración tangencial entre el instante inicial y un instante genérico:
integrando la aceleración tangencial entre el instante inicial y un instante genérico:

Por otra parte, la aceleración normal de una partícula viene dada por el cociente entre el cuadrado de su celeridad y el radio de curvatura de su trayectoria. Así que, conocidas en todo instante la celeridad 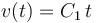 y la aceleración normal
y la aceleración normal 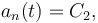 podemos determinar el radio de curvatura de la trayectoria como función del tiempo:
podemos determinar el radio de curvatura de la trayectoria como función del tiempo:
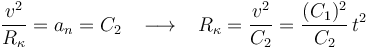
Observamos que, en el caso que nos ocupa, el radio de curvatura aumenta cuadráticamente con el tiempo. La respuesta correcta es la (c).





