No Boletín - Identificación de movimiento II (Ex.Nov/11)
De Laplace
Contenido |
1 Enunciado
Un punto material se mueve con ecuación horaria:
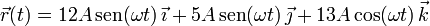
donde 
y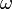 
son constantes conocidas.
- Determine la ley horaria s(t) suponiendo que s(0) = 0.
- Determine el triedro de Frenet y el radio de curvatura en cada instante.
- Identifique el tipo de movimiento.
2 Velocidad, celeridad y ley horaria
Derivando una vez el vector de posición respecto al tiempo, obtenemos el vector velocidad:
![\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\omega A\left[12\,\mathrm{cos}(\omega t)\,\vec{\imath}+5\,\mathrm{cos}(\omega t)\,\vec{\jmath}-13\,\mathrm{sen}(\omega t)\,\vec{k}\,\right]](/wiki/images/math/2/6/d/26db938f82a0c6ce4a60a1cec35b9cf4.png)
Y tomando módulo, calculamos la celeridad:
![v=|\vec{v}\,|=\omega A\sqrt{144\,\mbox{cos}^2(\omega t)+25\,\mbox{cos}^2(\omega t)+169\,\mbox{sen}^2(\omega t)}=\omega A\sqrt{169\,\left[\mbox{cos}^2(\omega t)+\mbox{sen}^2(\omega t)\right]}=13\,\omega A](/wiki/images/math/7/6/1/761a1bbafa5acb927a5b8aea32abdbd9.png)
Para deducir la ley horaria, basta recordar que la celeridad es precisamente la derivada temporal del parámetro arco:
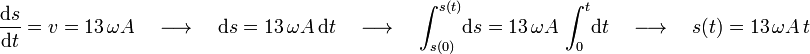
Al ser la celeridad de la partícula constante, se trata de un movimiento uniforme.
3 Aceleración y sus componentes intrínsecas
Derivando respecto al tiempo el vector velocidad, obtenemos el vector aceleración:
![\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=-\omega^2\! A\left[12\,\mathrm{sen}(\omega t)\,\vec{\imath}+5\,\mathrm{sen}(\omega t)\,\vec{\jmath}+13\,\mathrm{cos}(\omega t)\,\vec{k}\right]](/wiki/images/math/9/2/9/929813ebbfcd15cf30876df94f0f4b89.png)
Al tratarse de un movimiento uniforme, la aceleración tangencial es nula:
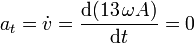
y entonces la aceleración normal (siempre positiva) coincide con el módulo del vector aceleración:
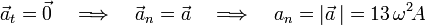
4 Triedro de Frenet
Obtenemos el vector tangente como un vector unitario en la dirección de la velocidad:
Dado que sabemos que toda la aceleración es normal (no existe componente tangencial), obtenemos el vector normal simplemente normalizando el vector aceleración:
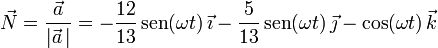
Por último, conocidos el vector tangente y el vector normal, hallamos el vector binormal como producto vectorial de ambos:
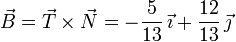
Vemos que resulta un vector binormal constante y, por tanto, podemos asegurar que la trayectoria es plana.
Nótese que otro procedimiento posible habría sido determinar primero el vector binormal normalizando el producto vectorial de velocidad por aceleración, y después calcular el vector normal como producto vectorial del binormal por el tangente.
5 Radio de curvatura
Hallamos el radio de curvatura a partir de la celeridad y la aceleración normal:
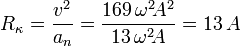
Obsérvese que el radio de curvatura resulta ser constante.
6 Identificación del movimiento
Puesto que la trayectoria es plana (vector binormal constante) y el radio de curvatura es constante, llegamos a la conclusión de que se trata de un movimiento circular. Es más, dado que la rapidez es constante, podemos asegurar que el movimiento es circular uniforme.
