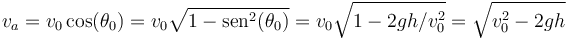No Boletín - Otro tiro parabólico II (proyectil y ave) (Ex.Nov/16)
De Laplace
1 Enunciado
Un proyectil y un ave se mueven simultáneamente en el plano vertical 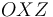 . El proyectil tiene una aceleración constante (de módulo
. El proyectil tiene una aceleración constante (de módulo  ) debida a la gravedad, y su posición y su velocidad iniciales son las correspondientes a un lanzamiento desde el
origen de coordenadas con celeridad inicial
) debida a la gravedad, y su posición y su velocidad iniciales son las correspondientes a un lanzamiento desde el
origen de coordenadas con celeridad inicial 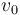 y con un ángulo
y con un ángulo 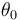 sobre el eje horizontal
sobre el eje horizontal  (siendo
(siendo 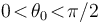 ):
):
![\vec{a}(t)=-\,g\,\vec{k}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\vec{r}\,(0)=\vec{0}\,\,\,;
\,\,\,\,\,\,\,\,\,\,\,\,\vec{v}\,(0)=v_{0}\,[\,\mathrm{cos}(\theta_0)\,\vec{\imath}+
\mathrm{sen}(\theta_0)\,\vec{k}\,]](/wiki/images/math/b/f/b/bfbc1212e30dc0f75be9e1c4f279a2f1.png)
Por otra parte, el ave vuela con celeridad constante 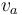 y manteniendo una altura constante
y manteniendo una altura constante  , y su posición inicial está en la vertical del punto de lanzamiento del proyectil, es decir:
, y su posición inicial está en la vertical del punto de lanzamiento del proyectil, es decir:

Considerando que  ,
, 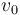 y
y  tienen valores positivos conocidos, y sabiendo que el ave recibe el impacto del proyectil justo en el instante en el que éste alcanza la posición de máxima altura en su trayectoria parabólica, determine (en función de
tienen valores positivos conocidos, y sabiendo que el ave recibe el impacto del proyectil justo en el instante en el que éste alcanza la posición de máxima altura en su trayectoria parabólica, determine (en función de  ,
, 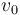 y
y  ):
):
- El ángulo
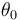 de lanzamiento del proyectil.
de lanzamiento del proyectil.
- La celeridad constante
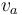 del ave.
del ave.
2 Ángulo de lanzamiento del proyectil
Las definiciones de velocidad instantánea y aceleración instantánea establecen que:

En el caso que nos ocupa, conocemos los valores iniciales de la posición 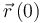 y de la velocidad
y de la velocidad 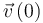 del proyectil, y además conocemos su aceleración en todo instante, la cual tiene valor constante:
del proyectil, y además conocemos su aceleración en todo instante, la cual tiene valor constante:
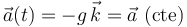
Determinar la velocidad y la posición del proyectil para 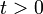 se reduce a integrar la aceleración una y dos veces, respectivamente, entre el instante inicial y un instante genérico:
se reduce a integrar la aceleración una y dos veces, respectivamente, entre el instante inicial y un instante genérico:
![\begin{array}{lllll} \mathrm{d}\vec{v}=\vec{a}\,\mathrm{d}t & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{v}(0)}^{\vec{v}(t)}\!\mathrm{d}\vec{v}=\vec{a}\displaystyle\int_{0}^{\, t}\mathrm{d}t & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{v}(t)=\vec{v}(0)+\vec{a}\,t \\ \\
\mathrm{d}\vec{r}=[\vec{v}(0)+\vec{a}\,t\,]\,\mathrm{d}t & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{r}(0)}^{\vec{r}(t)}\!\mathrm{d}\vec{r}=\vec{v}(0)\displaystyle\int_{0}^{\, t}\mathrm{d}t+\vec{a}\displaystyle\int_{0}^{\, t}\!t\,\mathrm{d}t & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{r}(t)=\vec{r}(0)+\vec{v}(0)\,t+\displaystyle\frac{1}{2}\,\vec{a}\,t^2\end{array}](/wiki/images/math/5/6/d/56dbaf75daf1c76dbb64c9e7fc54f8c8.png)
Sustituyendo los valores dados de 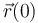 y
y 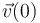 , obtenemos:
, obtenemos:
![\vec{v}(t)=v_0\,\mathrm{cos}(\theta_0)\,\vec{\imath}\,\,+\,\left[v_0\,\mathrm{sen}(\theta_0)-gt\,\right]\vec{k}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\vec{r}(t)=v_0\,\mathrm{cos}(\theta_0)\,t\,\,\vec{\imath}\,\,+\left[v_0\,\mathrm{sen}(\theta_0)\,t-\displaystyle\frac{1}{2}\,gt^2\right]\vec{k}](/wiki/images/math/5/f/a/5fa8cb80eb7f0ed687c099371e922967.png)
El proyectil alcanzará la posición de máxima altura en el instante 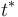 en el que la componente vertical de su velocidad se anule (condición de máximo para la coordenada
en el que la componente vertical de su velocidad se anule (condición de máximo para la coordenada  del proyectil):
del proyectil):
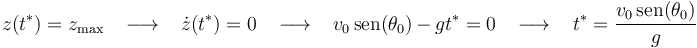
Por tanto, la máxima altura del proyectil es:
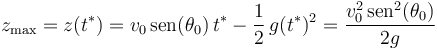
Y exigiendo que la máxima altura del proyectil coincida con la altura  a la que vuela el ave, determinamos el ángulo
a la que vuela el ave, determinamos el ángulo 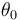 de lanzamiento del proyectil:
de lanzamiento del proyectil:
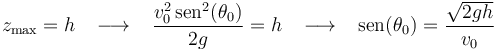
3 Celeridad constante del ave
Las componentes horizontales de las velocidades del proyectil (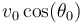 ) y del ave (
) y del ave (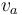 ) son ambas constantes. Por tanto, tienen que ser iguales entre sí para que las coordenadas
) son ambas constantes. Por tanto, tienen que ser iguales entre sí para que las coordenadas  del proyectil y del ave (coincidentes en
del proyectil y del ave (coincidentes en 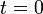 ) coincidan también en el instante del impacto:
) coincidan también en el instante del impacto: