No Boletín - Celeridad media en viaje mixto (Ex.Jun/13)

De Laplace

1 Enunciado

Un automóvil realiza un viaje de 100 km que consta de una primera parte sobre una carretera asfaltada y una segunda parte sobre un carril de tierra. En la carretera asfaltada avanza con una celeridad constante de 120 km/h, mientras que en el carril de tierra lo hace con una celeridad constante de 30 km/h. Sabiendo que la celeridad media en el trayecto total es de 75 km/h, ¿cuál es la longitud recorrida sobre el carril de tierra?

2 Solución

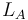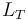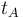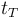Llamaremos $L_A\,$ y $L_T\,$ a las longitudes (en kilómetros) recorridas por el automóvil sobre asfalto y sobre tierra, respectivamente. Y llamaremos $t_A\,$ y $t_T\,$ a los tiempos (en horas) invertidos respectivamente en dichos recorridos.

Es dato la longitud total del viaje:

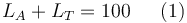
$L_A+L_T=100 \,\,\,\,\,\,\,\,\, (1)$

También sabemos por el enunciado que las celeridades en cada tramo son constantes y conocidas, lo cual nos permite relacionar longitud recorrida y tiempo invertido en cada parte del viaje:

$\frac{L_A}{t_A} = 120 \,\,\Longrightarrow\,\, t_A=\frac{L_A}{120}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{L_T}{t_T} = 30 \,\,\Longrightarrow\,\, t_T=\frac{L_T}{30}$

Por último, también es conocida la celeridad media en el trayecto total, es decir, el cociente entre la longitud total del viaje y el tiempo total empleado por el automóvil en realizarlo:

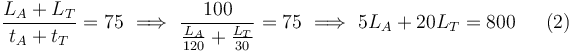
$\frac{L_A+L_T}{t_A+t_T} = 75 \,\,\Longrightarrow\,\, \frac{100}{\frac{L_A}{120}+\frac{L_T}{30}}=75 \,\,\Longrightarrow\,\, 5L_A+20L_T=800 \,\,\,\,\,\,\,\,\, (2)$

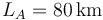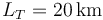
Resolviendo el sistema de ecuaciones (1)-(2), obtenemos los siguientes valores de las incógnitas: $\,\,L_A=80\,\mathrm{km}\,$ y $\,\,L_T=20\,\mathrm{km}\,$