2.10. Movimiento en espiral descrito en polares (Ex.Nov/11)

De Laplace

Contenido

1 Enunciado
2 Vector velocidad y rapidez del movimiento
3 Vector aceleración y sus componentes intrínsecas
4 Radio de curvatura

1 Enunciado

Una partícula recorre una espiral logarítmica, estando su posición en cada instante de tiempo descrita en coordenadas polares mediante las ecuaciones horarias:

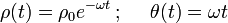
$\rho(t)=\rho_0e^{-\omega t}\,;\,\,\,\,\,\,\,\, \theta(t)=\omega t\,$

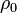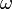donde $\rho_0\,$ y $\omega\,$ son constantes conocidas.

Calcule el vector velocidad y la rapidez del movimiento.
Halle el vector aceleración y sus componentes intrínsecas.
Calcule el radio de curvatura.

2 Vector velocidad y rapidez del movimiento

La velocidad en componentes polares viene dada por la expresión

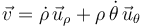
$\vec{v} = \dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta}$

Calculamos, por tanto, las primeras derivadas respecto al tiempo de las ecuaciones horarias

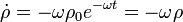
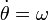
$\dot{\rho}=-\omega\rho_0 e^{-\omega t}=-\omega\rho$ $\dot{\theta}=\omega$

y sustituimos

$\vec{v} = -\omega\rho\,\vec{u}_{\rho}+\omega\rho\,\vec{u}_{\theta}$

Tomando módulo del vector velocidad, obtenemos la rapidez del movimiento

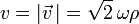
$v = |\vec{v}\,|=\sqrt{2}\,\omega\rho$

3 Vector aceleración y sus componentes intrínsecas

La aceleración en componentes polares viene dada por la expresión

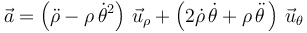
$\vec{a} = \left(\ddot{\rho}-\rho\,{\dot{\theta}}^2\right)\,\vec{u}_{\rho}+\left(2\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta}\,\right)\,\vec{u}_{\theta}$

Necesitamos también, por tanto, las segundas derivadas respecto al tiempo de las ecuaciones horarias

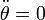
$\ddot{\rho}=\omega^{2}\! \rho_0 e^{-\omega t}=\omega^{2}\! \rho$ $\ddot{\theta}=0$

y sustituyendo y operando

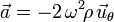
$\vec{a} = -2\,\omega^{2}\!\rho\,\vec{u}_{\theta}$

Para calcular la componente tangencial de la aceleración tenemos dos posibilidades: proyectar el vector aceleración sobre la dirección del vector velocidad (dirección tangente a la trayectoria), o bien derivar respecto al tiempo la rapidez previamente calculada:

$a_t=\frac{\vec{a}\cdot\vec{v}}{v}=\frac{-2\omega^3\!\rho^2}{\sqrt{2}\,\omega\rho}=-\sqrt{2}\,\omega^2\!\rho$ $a_t=\dot{v}=\sqrt{2}\,\omega\dot{\rho}=-\sqrt{2}\,\omega^2\!\rho$

Y entonces, la componente normal de la aceleración (siempre positiva) la podemos determinar a partir de:

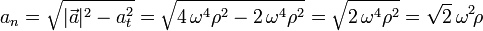
$a_n=\sqrt{|\vec{a}|^2-a_t^2}=\sqrt{4\,\omega^4\rho^2-2\,\omega^4\rho^2}=\sqrt{2\,\omega^4\rho^2}=\sqrt{2}\,\omega^2\!\rho$

4 Radio de curvatura

El radio de curvatura se puede calcular a partir del conocimiento de la componente normal de la aceleración y de la rapidez del movimiento:

$R_{\kappa}=\frac{v^{2}}{a_n}=\frac{2\,\omega^{2}\rho^2}{\sqrt{2}\,\omega^{2}\rho}=\sqrt{2}\,\rho$

2.10. Movimiento en espiral descrito en polares (Ex.Nov/11)

De Laplace

Contenido

1 Enunciado

2 Vector velocidad y rapidez del movimiento

3 Vector aceleración y sus componentes intrínsecas

4 Radio de curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES