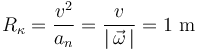No Boletín - Descripción vectorial de un movimiento circular (Ex.Nov/16)
De Laplace
1 Enunciado
Desde un triedro cartesiano  , se observa el movimiento circular de una partícula
, se observa el movimiento circular de una partícula  cuyo eje de giro pasa
por el origen de coordenadas
cuyo eje de giro pasa
por el origen de coordenadas  . En cierto instante, los vectores de posición, velocidad angular y aceleración angular de
. En cierto instante, los vectores de posición, velocidad angular y aceleración angular de  valen:
valen:
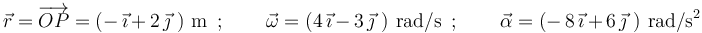
- ¿Cuánto vale la aceleración de la partícula en dicho instante?
- ¿Cuál es el radio de curvatura de su trayectoria?
2 Solución
Utilizando las fórmulas estudiadas en la teoría (descripción vectorial de un movimiento circular cuyo eje de giro pasa por el origen de coordenadas), podemos determinar la velocidad  , la aceleración tangencial
, la aceleración tangencial 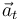 y la aceleración normal
y la aceleración normal 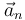 en el instante de interés:
en el instante de interés:

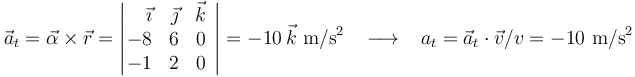
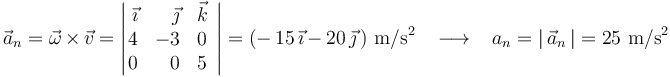
Por tanto, la aceleración 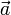 de la partícula en dicho instante vale:
de la partícula en dicho instante vale:
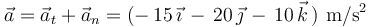
Y el radio de curvatura 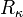 de su trayectoria (constante, por tratarse de una circunferencia) vale:
de su trayectoria (constante, por tratarse de una circunferencia) vale: