No Boletín - Rectilíneo con aceleración exponencialmente decreciente (Ex.Oct/15)
De Laplace
1 Enunciado
Una partícula, que se hallaba en reposo en el instante inicial (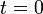 ), se mueve con una aceleración exponencialmente
decreciente en el tiempo según la fórmula:
), se mueve con una aceleración exponencialmente
decreciente en el tiempo según la fórmula:
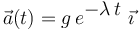
donde 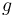 y
y 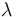 son constantes positivas conocidas.
son constantes positivas conocidas.
¿Hacia qué valor límite tiende la velocidad de dicha partícula cuando se deja pasar mucho tiempo (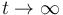 ) ?
) ?
2 Solución
Conforme a la definición de aceleración instantánea, podemos escribir:
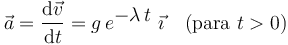
Conocemos también la velocidad inicial (la partícula se hallaba en reposo en 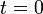 ):
):
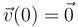
Determinamos la velocidad de la partícula para 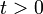 integrando su aceleración entre el instante inicial y un instante genérico:
integrando su aceleración entre el instante inicial y un instante genérico:

Por tanto, el valor límite hacia el que tiende la velocidad de la partícula cuando se deja pasar mucho tiempo (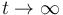 ) es:
) es:
![\vec{v}\,(\infty)=\lim_{t\rightarrow\infty}\vec{v}(t)=\lim_{t\rightarrow\infty}\left[\,\frac{g}{\lambda}\left(1-e^{\displaystyle -\lambda\, t}\right)\,\vec{\imath}\,\,\right]=\displaystyle\frac{g}{\lambda}\,\,\vec{\imath}](/wiki/images/math/3/f/5/3f59d4e63676add7f5f6c05b6d49d566.png)





