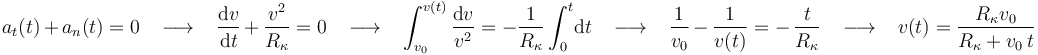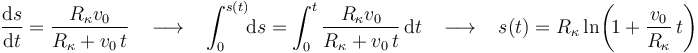No Boletín - Cuestión sobre componentes intrínsecas de la aceleración (Ex.Nov/16)

De Laplace

1 Enunciado

Una partícula, cuya celeridad inicial es 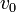$v_0\,$ , recorre una hélice de radio de curvatura 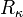$R_{\kappa}\,$ parametrizada naturalmente, de tal modo que se cumple la condición de que la suma de sus aceleraciones tangencial y normal es nula en todo instante de tiempo:

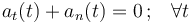
$a_t(t)+a_n(t)=0\,;\,\,\,\,\,\forall t$

¿Para cuál de las siguientes leyes horarias se cumple dicha condición?

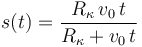
(1) $s(t)=\displaystyle\frac{R_{\kappa}\,v_0\,t}{R_{\kappa}+v_0\,t}\,$

(2) $s(t)=R_{\kappa}\,[\,e^{(v_0t/R_{\kappa})}-1\,]\,$

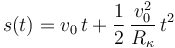
(3) $s(t)=v_0\,t+\displaystyle\frac{1}{2}\,\frac{v_0^2}{R_{\kappa}}\,t^2\,$

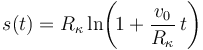
(4) $s(t)=R_{\kappa}\,\mathrm{ln}\!\left(\!1+\displaystyle\frac{v_0}{R_{\kappa}}\,t\right)\,$

2 Solución (por ensayo y error)

A partir de una ley horaria 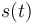$s(t)\,$ y del radio de curvatura 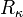$R_{\kappa}\,$ (constante en este caso, por tratarse de una hélice), podemos calcular la celeridad 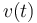$v(t)\,$ , la aceleración tangencial 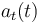$a_t(t)\,$ y la aceleración normal 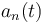$a_n(t)\,$ de la partícula:

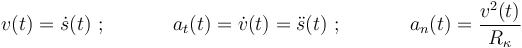
$v(t)=\dot{s}(t)\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a_t(t)=\dot{v}(t)=\ddot{s}(t)\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a_n(t)=\frac{v^2(t)}{R_{\kappa}}$

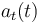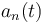Así que, tal como está planteado el ejercicio, basta con determinar $a_t(t)\,$ y $a_n(t)\,$ para cada una de las cuatro leyes horarias propuestas y comprobar en qué caso suman cero.

Para la ley horaria (1):

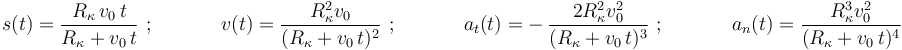
$s(t)=\displaystyle\frac{R_{\kappa}\,v_0\,t}{R_{\kappa}+v_0\,t}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, v(t)=\displaystyle\frac{R_{\kappa}^2 v_0}{(R_{\kappa}+v_0\,t)^2}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a_t(t)=-\,\displaystyle\frac{2 R_{\kappa}^2 v_0^2}{(R_{\kappa}+v_0\,t)^3}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a_n(t)=\displaystyle\frac{R_{\kappa}^3 v_0^2}{(R_{\kappa}+v_0\,t)^4}$

Para la ley horaria (2):

$s(t)=R_{\kappa}\,[\,e^{(v_0t/R_{\kappa})}-1\,]\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, v(t)=v_0\,e^{(v_0t/R_{\kappa})}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a_t(t)=\displaystyle\frac{v_0^2}{R_{\kappa}}\,e^{(v_0t/R_{\kappa})}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a_n(t)=\displaystyle\frac{v_0^2}{R_{\kappa}}\,e^{(2\,v_0t/R_{\kappa})}$

Para la ley horaria (3):

$s(t)=v_0\,t\,+\,\displaystyle\frac{1}{2}\,\frac{v_0^2}{R_{\kappa}}\,t^2\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, v(t)=v_0\,+\,\displaystyle\frac{v_0^2}{R_{\kappa}}\,t\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a_t(t)=\displaystyle\frac{v_0^2}{R_{\kappa}}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a_n(t)=\displaystyle\frac{1}{R_{\kappa}}\left(v_0+\displaystyle\frac{v_0^2}{R_{\kappa}}\,t\right)^2$

Para la ley horaria (4):

$s(t)=R_{\kappa}\,\mathrm{ln}\!\left(\!1+\displaystyle\frac{v_0}{R_{\kappa}}\,t\right)\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, v(t)=\displaystyle\frac{R_{\kappa}v_0}{R_{\kappa}+v_0\,t}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a_t(t)=-\,\displaystyle\frac{R_{\kappa}v_0^2}{(R_{\kappa}+v_0\,t)^2}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a_n(t)=\displaystyle\frac{R_{\kappa}v_0^2}{(R_{\kappa}+v_0\,t)^2}$

Es evidente que la condición $a_t(t)+a_n(t)=0\,$ sólo se verifica para la ley horaria (4).

3 Deducción directa de la ley horaria mediante integración

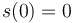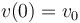A continuación, vamos a ver cómo se determinaría de forma directa la ley horaria que satisface la condición impuesta. Para ello, habría que integrar dos veces. Eso sí, para obtener una ley horaria concreta (sin constantes indeterminadas) es necesario que nos den las condiciones iniciales (en este caso, $s(0)=0\,$ , $v(0)=v_0\,$ ).

$a_t(t)\,+\,a_n(t)=0\,\,\,\,\,\longrightarrow\,\,\,\,\,\displaystyle\frac{\mathrm{d}v}{\mathrm{d}t}\,+\,\frac{v^2}{R_{\kappa}}=0\,\,\,\,\,\longrightarrow\,\,\,\,\,\int_{v_0}^{v(t)}\displaystyle\frac{\mathrm{d}v}{v^2}=-\frac{1}{R_{\kappa}}\int_{0}^{t}\!\mathrm{d}t\,\,\,\,\,\longrightarrow\,\,\,\,\,\displaystyle\frac{1}{v_0}\,-\,\frac{1}{v(t)}=-\,\frac{t}{R_{\kappa}}\,\,\,\,\,\longrightarrow\,\,\,\,\,v(t)=\frac{R_{\kappa}v_0}{R_{\kappa}+v_0\, t}$

$\frac{\mathrm{d}s}{\mathrm{d}t}=\frac{R_{\kappa}v_0}{R_{\kappa}+v_0\, t}\,\,\,\,\,\longrightarrow\,\,\,\,\,\int_{0}^{s(t)}\!\!\mathrm{d}s=\int_{0}^{t}\frac{R_{\kappa}v_0}{R_{\kappa}+v_0\, t}\,\mathrm{d}t\,\,\,\,\,\longrightarrow\,\,\,\,\,s(t)=R_{\kappa}\,\mathrm{ln}\!\left(\!1+\displaystyle\frac{v_0}{R_{\kappa}}\,t\right)$

No Boletín - Cuestión sobre componentes intrínsecas de la aceleración (Ex.Nov/16)

De Laplace

1 Enunciado

2 Solución (por ensayo y error)

3 Deducción directa de la ley horaria mediante integración

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES