No Boletín - Componentes intrínsecas en un movimiento circular (Ex.Jun/13)
De Laplace
1 Enunciado
El ángulo 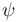 que forman entre sí los vectores velocidad y aceleración de una partícula puede determinarse a partir del cociente entre las componentes intrínsecas de su aceleración:
que forman entre sí los vectores velocidad y aceleración de una partícula puede determinarse a partir del cociente entre las componentes intrínsecas de su aceleración:
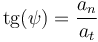
Sea una partícula  que recorre la circunferencia de radio
que recorre la circunferencia de radio  :
:
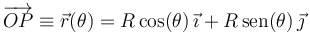
¿Para cuál de las siguientes leyes horarias se mantiene constante a lo largo del tiempo el ángulo 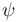 formado por la velocidad y la aceleración de la partícula? (Nota:
formado por la velocidad y la aceleración de la partícula? (Nota: 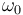 ,
, 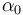 y
y  son constantes positivas conocidas.)
son constantes positivas conocidas.)
1) 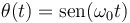
2) 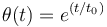
3) 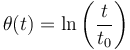
4) 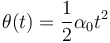
2 Solución
Al estudiar en la teoría la descripción angular del movimiento circular de una partícula, utilizábamos precisamente la ecuación  -paramétrica de la circunferencia a la que se refiere el enunciado de este problema. Y definíamos la velocidad angular
-paramétrica de la circunferencia a la que se refiere el enunciado de este problema. Y definíamos la velocidad angular 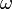 y la aceleración angular
y la aceleración angular 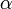 de la partícula como las derivadas temporales de primer y segundo orden, respectivamente, de la ley horaria
de la partícula como las derivadas temporales de primer y segundo orden, respectivamente, de la ley horaria 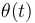 . También se dedujeron sendas expresiones para las componentes tangencial y normal de la aceleración de la partícula:
. También se dedujeron sendas expresiones para las componentes tangencial y normal de la aceleración de la partícula:

Entonces, conforme a la afirmación inicial del enunciado, el ángulo 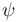 que forman entre sí los vectores velocidad y aceleración de una partícula que realiza el movimiento circular propuesto se determina mediante el siguiente cociente:
que forman entre sí los vectores velocidad y aceleración de una partícula que realiza el movimiento circular propuesto se determina mediante el siguiente cociente:
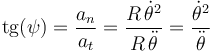
Por tanto, averiguaremos para cuál de las cuatro leyes horarias propuestas en el enunciado se mantiene constante a lo largo del tiempo el ángulo 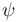 formado por la velocidad y la aceleración de la partícula investigando en cuál de ellas desaparece el tiempo al realizar el citado cociente:
formado por la velocidad y la aceleración de la partícula investigando en cuál de ellas desaparece el tiempo al realizar el citado cociente:
1) 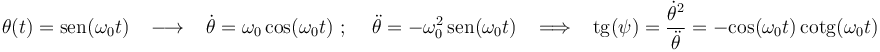
2) 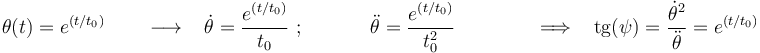
3) 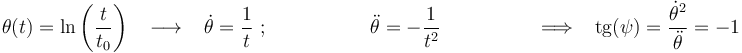
4) 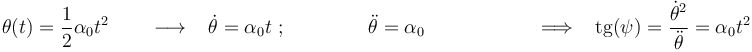
Como puede observarse, la respuesta correcta es la opción número 3.





