No Boletín - Celeridad media de un vehículo (Ex.Ene/12)

De Laplace

1 Enunciado

Un automóvil recorre cierto trayecto del siguiente modo: la mitad de su longitud con celeridad constante de 120 km/h, y la otra mitad con celeridad constante de 60 km/h. ¿Cuál ha sido su celeridad media en el recorrido total?

2 Solución

Si llamamos $L\,$ a la longitud total del trayecto, y $t\,$ al tiempo total empleado por el automóvil en recorrerlo, la celeridad media en el recorrido total es el cociente:

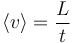
$\left\langle v\right\rangle = \frac{L}{t}$

Pero sabemos que la primera mitad de esa longitud se ha recorrido con una celeridad constante de 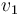$v_1\,$ = 120 km/h. ¿Qué tiempo $t 1$ habrá invertido el automóvil en recorrer esa primera mitad? La respuesta es inmediata dado que sabemos que la celeridad ha sido constante:

$v_1 = \frac{L/2}{t_1}\,\,\Longrightarrow\,\, t_1=\frac{L}{2v_1}$

¿Y qué tiempo $t 2$ habrá invertido el automóvil en recorrer la segunda mitad de la longitud del trayecto a una celeridad constante de 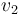$v_2\,$ = 60 km/h? Pues:

$v_2 = \frac{L/2}{t_2}\,\,\Longrightarrow\,\, t_2=\frac{L}{2v_2}$

Entonces, teniendo en cuenta que 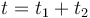$t=t_1+t_2\,$ y sustituyendo en la expresión inicial, obtenemos la celeridad media:

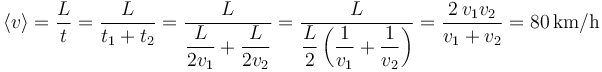
$\left\langle v\right\rangle = \frac{L}{t}=\frac{L}{t_1+t_2}=\frac{L}{\displaystyle\frac{L}{2v_1}+\displaystyle\frac{L}{2v_2}}=\frac{L}{\displaystyle\frac{L}{2}\left(\displaystyle\frac{1}{v_1}+\displaystyle\frac{1}{v_2}\right)}=\frac{2\,v_1v_2}{v_1+v_2}=80\, \mbox{km/h}$

Este resultado también se puede escribir en la forma más simétrica

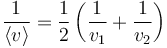
$\frac{1}{\langle v\rangle} = \frac{1}{2}\left(\frac{1}{v_1}+\frac{1}{v_2}\right)$

es decir, la media aritmética de las inversas de las celeridades es la inversa de la celeridad media.

No Boletín - Celeridad media de un vehículo (Ex.Ene/12)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES