Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Dos móviles sobre el eje OX acercándose (Ex.Oct/14)

De Laplace

Contenido

1 Enunciado

Un móvil A recorre el eje OX con una velocidad constante 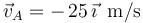\vec{v}_{A}=-\,25\,\vec{\imath}\,\,\,\mathrm{m}/\mathrm{s}\,, hallándose en el punto 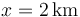x=2\,\mathrm{km}\, en el instante inicial 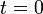t=0\,. En ese mismo instante un segundo móvil B, que se encuentra en reposo en el punto 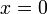x=0\,, comienza a moverse con una aceleración creciente en el tiempo según la fórmula:

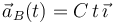
\vec{a}_B(t)=C\, t\,\vec{\imath}

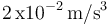donde C\, es una constante de valor igual a 2\,\mathrm{x}10^{-2}\,\mathrm{m}/\mathrm{s}^{3}\,.

  1. ¿Cuánto tiempo transcurre hasta el instante en el que la celeridad de B alcanza el mismo valor que la celeridad de A?
  2. ¿Qué distancia hay entre los móviles A y B en el instante al que se refiere la pregunta anterior?

2 Posiciones y velocidades en función del tiempo

Comenzaremos estudiando la cinemática del móvil B.

Conforme a las definiciones de velocidad instantánea y aceleración instantánea, podemos escribir:

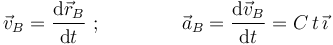
\vec{v}_B=\frac{\mathrm{d}\vec{r}_B}{\mathrm{d}t}\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}_B=\frac{\mathrm{d}\vec{v}_B}{\mathrm{d}t}=C\, t\,\vec{\imath}

Conocemos también las condiciones iniciales de posición y velocidad:

\vec{r}_B(0)=\vec{0}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{v}_B(0)=\vec{0}

Por tanto, determinar la velocidad y la posición del móvil B en función del tiempo se reduce a integrar su aceleración una y dos veces, respectivamente, entre el instante inicial y el instante genérico t\,:

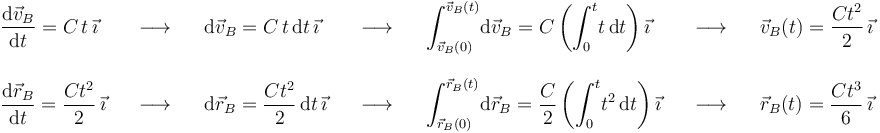
\begin{array}{lllllll}\displaystyle\frac{\mathrm{d}\vec{v}_B}{\mathrm{d}t}=C\, t\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \mathrm{d}\vec{v}_B=C\, t\,\mathrm{d}t\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{v}_B(0)}^{\vec{v}_B(t)}\!\mathrm{d}\vec{v}_B=C\left(\displaystyle\int_{0}^{t}\!t\,\mathrm{d}t\right)\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{v}_B(t)=\displaystyle\frac{Ct^2}{2}\,\vec{\imath} \\ \\ \displaystyle\frac{\mathrm{d}\vec{r}_B}{\mathrm{d}t}=\frac{Ct^2}{2}\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \mathrm{d}\vec{r}_B=\displaystyle\frac{Ct^2}{2}\,\mathrm{d}t\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{r}_B(0)}^{\vec{r}_B(t)}\!\mathrm{d}\vec{r}_B=\frac{C}{2}\left(\displaystyle\int_{0}^{t}\!t^2\,\mathrm{d}t\right)\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{r}_B(t)=\displaystyle\frac{Ct^3}{6}\,\vec{\imath}\end{array}

La cinemática del móvil A es más sencilla, dado que realiza un movimiento rectilíneo uniforme:

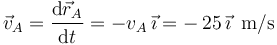
\vec{v}_A=\frac{\mathrm{d}\vec{r}_A}{\mathrm{d}t}=-v_A\,\vec{\imath}=-\,25\,\vec{\imath}\,\,\,\mathrm{m}/\mathrm{s}

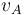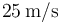donde hemos llamado v_A\, a la celeridad constante del móvil A (cuyo valor es 25\,\mathrm{m}/\mathrm{s}\,).

Conocemos también la condición inicial de posición:

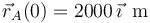
\vec{r}_A(0)=2000\,\vec{\imath}\,\,\,\mathrm{m}

La posición del móvil A en función del tiempo se obtiene integrando su velocidad entre el instante inicial y el instante genérico t\,:

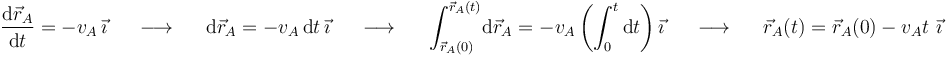
\begin{array}{lllllll} \displaystyle\frac{\mathrm{d}\vec{r}_A}{\mathrm{d}t}=-v_A\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \mathrm{d}\vec{r}_A=-v_A\,\mathrm{d}t\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{r}_A(0)}^{\vec{r}_A(t)}\!\mathrm{d}\vec{r}_A=-v_A\left(\displaystyle\int_{0}^{t}\mathrm{d}t\right)\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{r}_A(t)=\vec{r}_A(0)-v_A t\,\,\vec{\imath}\end{array}

3 Instante en el que se igualan las celeridades de los dos móviles

Conocidas las velocidades de A y B en función del tiempo:

\vec{v}_A(t)=-v_A\,\vec{\imath}\,\,; \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{v}_B(t)=\displaystyle\frac{Ct^2}{2}\,\vec{\imath}

es fácil determinar en qué instante (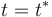\,t=t^*\,) la celeridad de B alcanza el mismo valor que la celeridad de A:

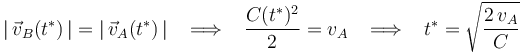
|\,\vec{v}_B(t^*)\,|=|\,\vec{v}_A(t^*)\,|\,\,\,\,\,\Longrightarrow\,\,\,\,\,\frac{C(t^*)^2}{2}=v_A\,\,\,\,\,\Longrightarrow\,\,\,\,\,t^*=\sqrt{\frac{2\,v_A}{C}}

y sustituyendo los datos numéricos:

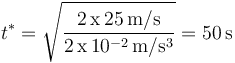
t^*=\sqrt{\frac{2\,\mathrm{x}\,25\,\mathrm{m}/\mathrm{s}}{2\,\mathrm{x}\,10^{-2}\,\mathrm{m}/\mathrm{s}^{3}}}=50\,\mathrm{s}

4 Distancia entre ambos móviles en dicho instante

Conocidas las posiciones de A y B en función del tiempo:

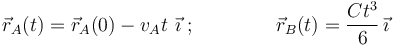
\vec{r}_A(t)=\vec{r}_A(0)-v_A t\,\,\vec{\imath}\,\,; \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{r}_B(t)=\displaystyle\frac{Ct^3}{6}\,\vec{\imath}

es fácil determinar la distancia 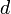d\, existente entre ambos móviles en el instante t=t^*\,:

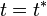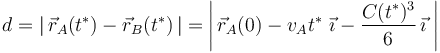
d=|\,\vec{r}_A(t^*)-\vec{r}_B(t^*)\,|=\left|\,\vec{r}_A(0)-v_A t^*\,\,\vec{\imath}-\frac{C(t^*)^3}{6}\,\vec{\imath}\,\,\right|

y sustituyendo los datos numéricos:

d=\left|\,\left[\,2000\,\mathrm{m}-25\,\mathrm{m}/\mathrm{s}\,\,\mathrm{x}\,\, 50\,\mathrm{s}-\frac{2\,\mathrm{x}\,10^{-2}\,\mathrm{m}/\mathrm{s}^{3}\,\,\mathrm{x}\,\,(50\,\mathrm{s})^3}{6}\,\right]\vec{\imath}\,\,\right|=333.3\,\mathrm{m}
Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Dos_m%C3%B3viles_sobre_el_eje_OX_acerc%C3%A1ndose_(Ex.Oct/14)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 13:47, 16 mar 2015. - Esta página ha sido visitada 3.706 veces. - Aviso legal - Acerca de Laplace