Electrostática en el vacío
De Laplace
(→Principio de superposición de campos) |
(→Densidad de carga) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 15: | Línea 15: | ||
\varepsilon_0 = 8.85\times 10^{-12}\frac{\mathrm{C}^2}{\mathrm{N}{\cdot}\mathrm{m}}=\frac{1}{36\pi\times 10^9} \frac{\mathrm{C}^2}{\mathrm{N}{\cdot}\mathrm{m}}</math></center> | \varepsilon_0 = 8.85\times 10^{-12}\frac{\mathrm{C}^2}{\mathrm{N}{\cdot}\mathrm{m}}=\frac{1}{36\pi\times 10^9} \frac{\mathrm{C}^2}{\mathrm{N}{\cdot}\mathrm{m}}</math></center> | ||
| - | ==Principio de superposición | + | ==Principio de superposición== |
| - | El segundo pilar es el principio de superposición, que establece que si tenemos un conjunto de cargas <math>q_i</math>. La fuerza sobre una de ellas, <math>q_0</math>, es la suma vectorial de las fuerzas producidas por las demás, calculadas separadamente según la ley de Coulomb. | + | El segundo pilar es el ''principio de superposición'', que establece que si tenemos un conjunto de cargas <math>q_i</math>. La fuerza sobre una de ellas, <math>q_0</math>, es la suma vectorial de las fuerzas producidas por las demás, calculadas separadamente según la ley de Coulomb. |
==Densidad de carga== | ==Densidad de carga== | ||
| + | En situaciones macroscópicas, en lugar de tratar la ingente cantidad de cargas de la materia de forma individual, se define la densidad de carga | ||
| + | |||
| + | <center><math>\rho(\mathbf{r}) = \frac{1}{\Delta\tau}\sum_{q_i\in\Delta\tau} q_i</math></center> | ||
| + | |||
| + | Este promedio se calcula sumando todas las cargas contenidas en un elemento de volumen <math>\Delta\tau</math>, lo suficientemente pequeño para ser considerado como microscópico, y lo bastante grande como para contener miles de cargas (un tamaño típico puede ser <math>\Delta\tau \sim 1\,\mu\mathrm{m}^3</math>). El elemento de volumen se encuentra centrado en un punto <math>\mathbf{r}'</math>, de esta forma la densidad de carga se trata como un campo escalar <math>\rho(\mathbf{r}')</math>. | ||
| + | |||
| + | Si las cargas están concentradas en una superficie o a lo largo de una curva, se definen las densidades de carga superficial y lineal | ||
| + | |||
| + | <center><math>\sigma_s(\mathbf{r}') = \frac{1}{\Delta S}\sum_{q_i\in\Delta S} q_i</math>{{qquad}}{{qquad}}<math>\lambda(\mathbf{r}') = \frac{1}{\Delta l}\sum_{q_i\in\Delta l} q_i</math></center> | ||
| + | |||
| + | Varios tipos de distribuciones pueden coexistir. | ||
| + | |||
==Campo eléctrico de cargas en reposo== | ==Campo eléctrico de cargas en reposo== | ||
última version al 20:17 6 feb 2010
1 Concepto de carga eléctrica
2 Ley de Coulomb
Los principios básicos de interacción entre cargas puntuales son dos.
El primero, establecido por Cavendish y por Coulomb, recibe el nombre de este último y da la fuerza entre dos cargas puntuales
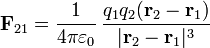
siendo 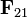 la fuerza que experimenta la carga 2 debida a la
carga 1. La fuerza
la fuerza que experimenta la carga 2 debida a la
carga 1. La fuerza 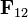 es igual, pero de sentido contrario.
es igual, pero de sentido contrario.
En el sistema internacional las cargas se miden en culombios, y la constante universal  tiene por valor
tiene por valor
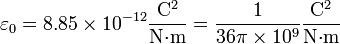
3 Principio de superposición
El segundo pilar es el principio de superposición, que establece que si tenemos un conjunto de cargas qi. La fuerza sobre una de ellas, q0, es la suma vectorial de las fuerzas producidas por las demás, calculadas separadamente según la ley de Coulomb.
4 Densidad de carga
En situaciones macroscópicas, en lugar de tratar la ingente cantidad de cargas de la materia de forma individual, se define la densidad de carga
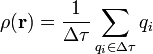
Este promedio se calcula sumando todas las cargas contenidas en un elemento de volumen Δτ, lo suficientemente pequeño para ser considerado como microscópico, y lo bastante grande como para contener miles de cargas (un tamaño típico puede ser 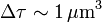 ). El elemento de volumen se encuentra centrado en un punto
). El elemento de volumen se encuentra centrado en un punto 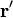 , de esta forma la densidad de carga se trata como un campo escalar
, de esta forma la densidad de carga se trata como un campo escalar 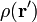 .
.
Si las cargas están concentradas en una superficie o a lo largo de una curva, se definen las densidades de carga superficial y lineal
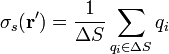
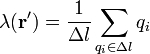
Varios tipos de distribuciones pueden coexistir.





