Energía de esferas concéntricas

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Halle la energía electrostática almacenada en una superficie esférica de radio

a

, que almacena una carga

Q

, distribuida uniformemente sobre ella.

Calcule la energía electrostática almacenada en un sistema de dos superficies esféricas concéntricas de radios $a$ y $b$ , cargadas, respectivamente con cargas $+ Q$ y $- Q$ , distribuidas uniformemente.

¿Se verifica el principio de superposición, esto es, es la energía de las dos esferas la suma de las energías de cada esfera por separado?

2 Solución

2.1 Energía de una superficie esférica

La energía electrostática de una distribución de carga superficial viene dada por

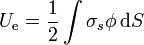
$U_\mathrm{e} = \frac{1}{2}\int \sigma_s \phi\,\mathrm{d}S$

siendo $\phi\,$ el potencial en los puntos en que se encuentran las cargas. En el caso de una superficie esférica cargada uniformemente, el potencial que crea en todos los puntos del espacio, tal como se ve en otro problema es

$\phi = \begin{cases}\displaystyle\frac{Q}{4\pi\varepsilon_0 a} & r \leq a \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r} & r \geq a\end{cases}$

En los puntos de la superficie esférica $r = a$ vale tanto la expresión interior como la exterior por ser el potencial una función continua

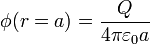
$\phi(r=a) = \frac{Q}{4\pi\varepsilon_0 a}$

y por ello la energía electrostática almacenada por la esfera es

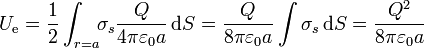
$U_\mathrm{e} = \frac{1}{2}\int_{r=a}\!\! \sigma_s \frac{Q}{4\pi\varepsilon_0 a}\,\mathrm{d}S = \frac{Q}{8\pi\varepsilon_0a}\int\sigma_s\,\mathrm{d}S = \frac{Q^2}{8\pi\varepsilon_0a}$

dado que el potencial tiene el mismo valor en todos los puntos de la superficie, puede salir de la integral. El resultado es una función cuadrática de la carga. Esto quiere decir que, tanto si la superficie esférica esta cargada positivamente, como si lo está negativamente, la energía es siempre positiva.

2.2 Energía de dos esferas concéntricas

Para dos superficies esféricas la energía será de la forma

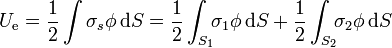
$U_\mathrm{e} = \frac{1}{2}\int \sigma_s \phi\,\mathrm{d}S=\frac{1}{2}\int_{S_1}\!\! \sigma_1 \phi\,\mathrm{d}S+\frac{1}{2}\int_{S_2}\!\! \sigma_2 \phi\,\mathrm{d}S$

donde el potencial que aparece en cada integral es el total de la distribución (esto es, incluye tanto la contribución de la propia esfera como la de la otra). Obtenemos este potencial por el principio de superposición

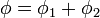
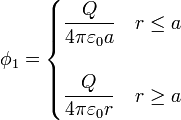
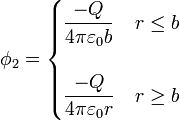
$\phi = \phi_1 + \phi_2\,$ $\phi_1 = \begin{cases}\displaystyle\frac{Q}{4\pi\varepsilon_0 a} & r \leq a \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r} & r \geq a\end{cases}$ $\phi_2 = \begin{cases}\displaystyle\frac{-Q}{4\pi\varepsilon_0 b} & r \leq b \\ & \\ \displaystyle\frac{-Q}{4\pi\varepsilon_0 r} & r \geq b\end{cases}$

Sumando, resultan tres regiones,

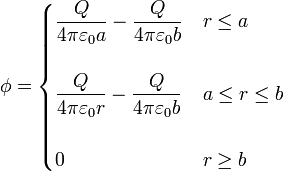
$\phi = \begin{cases}\displaystyle\frac{Q}{4\pi\varepsilon_0 a} -\frac{Q}{4\pi\varepsilon_0b} & r \leq a \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r} -\frac{Q}{4\pi\varepsilon_0b} & a \leq r \leq b \\ & \\ 0 & r \geq b\end{cases}$

Los potenciales a los que se encuentran las superficies son, respectivamente:

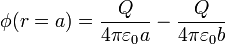
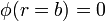
$\phi(r=a)=\frac{Q}{4\pi\varepsilon_0 a} -\frac{Q}{4\pi\varepsilon_0b}$ $\phi(r=b)=0\,$

y la energía electrostática almacenada

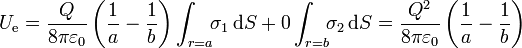
$U_\mathrm{e}= \frac{Q}{8\pi\varepsilon_0}\left(\frac{1}{a}-\frac{1}{b}\right)\int_{r=a}\!\! \sigma_1\,\mathrm{d}S + 0 \int_{r=b}\!\! \sigma_2\,\mathrm{d}S = \frac{Q^2}{8\pi\varepsilon_0}\left(\frac{1}{a}-\frac{1}{b}\right)$

Podría parecer, en una primera inspección, que el resultado es la suma de las energía de cada esfera por separado, siendo negativa la de la esfera cargada negativamente, pero esto es erróneo. Según dijimos en el apartado anterior, la energía de una esfera cargada, sea su carga positiva o negativa, es siempre positiva, por lo que la suma de energías individuales debería aparecer con un signo positivo. No se verifica el principio de superposición.

Podemos desarrollar esto matemáticamente, aplicando el principio de superposición a los potenciales, de forma que queda

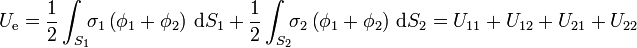
$U_\mathrm{e} = \frac{1}{2}\int_{S_1}\!\! \sigma_1 \left(\phi_1+\phi_2\right)\,\mathrm{d}S_1+\frac{1}{2}\int_{S_2}\!\! \sigma_2 \left(\phi_1+\phi_2\right)\,\mathrm{d}S_2= U_{11}+U_{12}+U_{21}+U_{22}$

Los términos

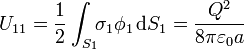
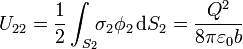
$U_{11}=\frac{1}{2}\int_{S_1}\!\! \sigma_1 \phi_1\,\mathrm{d}S_1 = \frac{Q^2}{8\pi\varepsilon_0a}$ $U_{22}=\frac{1}{2}\int_{S_2}\!\! \sigma_2 \phi_2\,\mathrm{d}S_2 = \frac{Q^2}{8\pi\varepsilon_0b}$

sí representan las energías individuales de cada esfera y son ambos positivos. No obstante, la energía total incluye además dos términos cruzados, correspondientes a la interacción entre las dos esferas

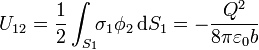
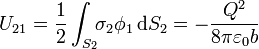
$U_{12}=\frac{1}{2}\int_{S_1}\!\! \sigma_1 \phi_2\,\mathrm{d}S_1 = -\frac{Q^2}{8\pi\varepsilon_0b}$ $U_{21}=\frac{1}{2}\int_{S_2}\!\! \sigma_2 \phi_1\,\mathrm{d}S_2 = -\frac{Q^2}{8\pi\varepsilon_0b}$

Estos dos términos son negativos, como corresponde a la interacción de cargas de signo opuesto, son iguales entre sí (lo que constituye una relación de reciprocidad, que es una propiedad general de la energía electrostática), y son responsables de que en la expresión completa de la energía aparezca un signo negativo.

2.3 Cálculo empleando el campo eléctrico

La energía electrostática de un sistema también se puede calcular a partir de la densidad de energía, como función del campo eléctrico

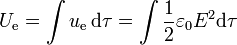
$U_\mathrm{e}=\int u_\mathrm{e}\,\mathrm{d}\tau = \int \frac{1}{2}\varepsilon_0 E^2\mathrm{d}\tau$

donde esta integral de volumen se extiende a todo el espacio.

2.3.1 Caso de una sola esfera

Si tenemos una sola esfera cargada, el campo que produce es,

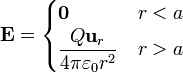
$\mathbf{E}=\begin{cases}\mathbf{0} & r < a \\ \displaystyle \frac{Q\mathbf{u}_r}{4\pi\varepsilon_0 r^2} & r > a\end{cases}$

de modo que la densidad de energía electrostática vale

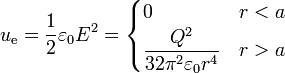
$u_\mathrm{e}= \frac{1}{2}\varepsilon_0 E^2 = \begin{cases}0 & r < a \\ \displaystyle \frac{Q^2}{32\pi^2\varepsilon_0 r^4} & r > a\end{cases}$

La integral de esta densidad, extendida a todo el espacio, se compone de dos partes

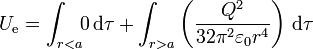
$U_\mathrm{e}= \int_{r<a} \!\! 0\,\mathrm{d}\tau + \int_{r>a} \left(\frac{Q^2}{32\pi^2\varepsilon_0 r^4}\right)\,\mathrm{d}\tau$

La contribución del campo interior es evidentemente nula. La contribución debida al campo exterior es

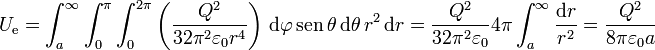
$U_\mathrm{e}= \int_a^\infty \int_0^\pi \int_0^{2\pi} \left(\frac{Q^2}{32\pi^2\varepsilon_0 r^4}\right)\,\mathrm{d}\varphi\,\mathrm{sen}\,\theta\,\mathrm{d}\theta\,r^2\,\mathrm{d}r= \frac{Q^2}{32\pi^2\varepsilon_0}4\pi\int_a^\infty \frac{\mathrm{d}r}{r^2} = \frac{Q^2}{8\pi\varepsilon_0 a}$

2.3.2 Caso de dos esferas concéntricas

Para el caso de dos esferas concéntricasl, hallamos el campo por superposición. La única diferencia con el de una esfera es que, en el exterior de las dos esferas, el campo de la esfera negativa cancela exactmante el campo de la positiva 8ambos son como el de una carga puntual), anulando el campo en el exterior

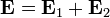
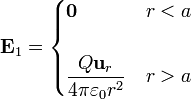
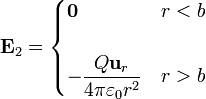
$\mathbf{E}=\mathbf{E}_1+\mathbf{E}_2$ $\mathbf{E}_1=\begin{cases}\mathbf{0} & r < a \\ & \\\displaystyle \frac{Q\mathbf{u}_r}{4\pi\varepsilon_0 r^2} & r > a\end{cases}$ $\mathbf{E}_2=\begin{cases}\mathbf{0} & r < b \\& \\ \displaystyle -\frac{Q\mathbf{u}_r}{4\pi\varepsilon_0 r^2} & r > b\end{cases}$

Sumando, quedan de nuevo tres regiones para el campo y la densidad de energía

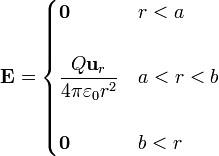
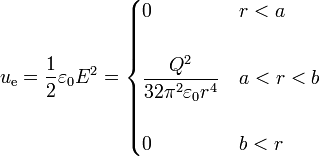
$\mathbf{E}=\begin{cases}\mathbf{0} & r < a \\ & \\ \displaystyle \frac{Q\mathbf{u}_r}{4\pi\varepsilon_0 r^2} & a < r < b \\ & \\ \mathbf{0} & b < r\end{cases}$ $u_\mathrm{e}=\frac{1}{2}\varepsilon_0E^2 = \begin{cases}0 & r < a \\ & \\ \displaystyle \frac{Q^2}{32\pi^2\varepsilon_0 r^4} & a < r < b \\ & \\ 0 & b < r\end{cases}$

Vemos que la densidad de energía entre las esferas es la misma que en el caso de una sola esfera (porque el campo es el mismo), mientras que en el exterior ha pasado de tener un cierto valor a ser nula. Por tanto, la energía electrostática total es la integral de la misma densidad de energía que en el apartado anterior pero solo en la región entre las esferas, esto es

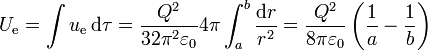
$U_\mathrm{e} = \int u_\mathrm{e}\,\mathrm{d}\tau =\frac{Q^2}{32\pi^2\varepsilon_0}4\pi\int_a^b \frac{\mathrm{d}r}{r^2} = \frac{Q^2}{8\pi\varepsilon_0}\left(\frac{1}{a}-\frac{1}{b}\right)$

Podemos entender este resultado como que la energía en el sistema de las dos esferas es la energía almacenada en el exterior de una sola esfera de radio $a$ (calculada antes) menos la energía almacenada en el exterior de la esfera de radio $b$ , porque para $r > b$ la densidad de energía es ahora nula.

Energía de esferas concéntricas

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Energía de una superficie esférica

2.2 Energía de dos esferas concéntricas

2.3 Cálculo empleando el campo eléctrico

2.3.1 Caso de una sola esfera

2.3.2 Caso de dos esferas concéntricas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES