Campo debido a una superficie esférica cargada

De Laplace

Contenido

1 Enunciado
2 Aplicando las leyes de la electrostática
3 Por integración directa

1 Enunciado

Una esfera de radio $R$ almacena una carga $Q$ distribuida uniformemente en su superficie. Calcule el campo eléctrico producido por la esfera en todos los puntos del espacio

Aplicando las leyes de la electrostática
Por integración directa

2 Aplicando las leyes de la electrostática

La forma más sencilla de calcular este campo es aplicando el caracter irrotacional del campo electrostático y la ley de Gauss.

El hecho de que el campo electrostático es irrotacional nos permite introducir el potencial eléctrico

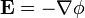
$\nabla\times\mathbf{E}=\mathbf{0}$ $\mathbf{E}=-\nabla\phi$

El uso del potencial eléctrico nos permite aprovechar de forma sencilla las simetrías de este problema.

Por tratarse de una superficie esférica uniformemente cargada, el sistema es invariante ante una rotación alrededor de su centro. Por ello, el potencial eléctrico no puede depender de las coordenadas esféricas $θ$ y $\varphi$

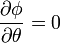
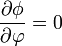
$\frac{\partial \phi}{\partial\theta} = 0$ $\frac{\partial \phi}{\partial\varphi} = 0$

Por tanto, el potencial eléctrico depende exclusivamente de la distancia al centro de la esfera

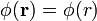
$\phi(\mathbf{r}) = \phi(r)$

y esto implica que el campo electrostático es un campo central

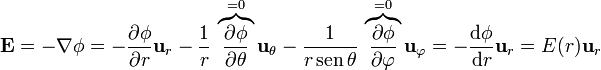
$\mathbf{E}=-\nabla\phi = - \frac{\partial \phi}{\partial r}\mathbf{u}_r - \frac{1}{r}\,\overbrace{\frac{\partial \phi}{\partial\theta}}^{=0}\mathbf{u}_\theta -\frac{1}{r\,\mathrm{sen}\,\theta}\,\overbrace{\frac{\partial \phi}{\partial\varphi}}^{=0}\mathbf{u}_\varphi = -\frac{\mathrm{d}\phi}{\mathrm{d}r}\mathbf{u}_r = E(r)\mathbf{u}_r$

Una vez establecido que el campo es radial y dependiente exclusivamente de la distancia al centro, podemos utilizar la ley de Gauss para hallar su valor.

Supongamos una superficie esférica de radio $r$ , concéntrica con la esfera de carga (pero de radio diferente, $r$ puede tener cualquier valor, mayor o menor que $R$ , el radio de la esfera cargada). De acuerdo con la ley de Gauss

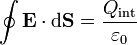
$\oint \mathbf{E}\cdot\mathrm{d}\mathbf{S}= \frac{Q_\mathrm{int}}{\varepsilon_0}$

Vamos primero con el segundo miembro. $Q int$ es la carga encerrada por la superficie sobre la que estamos hallando el flujo. Tenemos dos posibilidades:

$r > R$ La superficie de integración es exterior a la superficie cargada. En este caso, encierra a toda la distribución y $Q int$ es la carga total de la distribución

$Q_\mathrm{int} = Q\qquad(r>R)$

$r < R$ La superficie de integración es interior a la esfera y no encierra carga alguna, pues toda esta en el exterior de la superficie

$Q_\mathrm{int} = 0\qquad(r<R)$

Agrupando ambos resultados

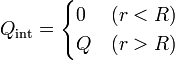
$Q_\mathrm{int} = \begin{cases}0 & (r < R) \\ Q & (r>R)\end{cases}$

Vamos ahora con el primer miembro. Para una superficie esférica tenemos que

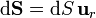
$\mathrm{d}\mathbf{S} = \mathrm{d}S\,\mathbf{u}_{r}$

por lo que el flujo se reduce a la integral

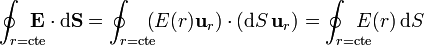
$\oint_{r=\mathrm{cte}}\!\!\!\!\!\!\mathbf{E}\cdot\mathrm{d}\mathbf{S} = \oint_{r=\mathrm{cte}}\!\!\!\!\left(E(r)\mathbf{u}_r\right)\cdot\left(\mathrm{d}S\,\mathbf{u}_r\right) = \oint_{r=\mathrm{cte}}\!\!\!\!\!\!E(r)\,\mathrm{d}S$

En esta última integral yta no aparece el campo como vector, que varía de punto a punto de la superficie esférica (pues su dirección cambia de punto a punto), sino solo su componente radial, que sí tiene el mismo valor para todos los puntos de la superficie esférica (por ser $\mathbf{E}$ un campo central). Por tanto, puede salir de la integral

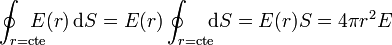
$\oint_{r=\mathrm{cte}}\!\!\!\!\!\!E(r)\,\mathrm{d}S = E(r) \oint_{r=\mathrm{cte}}\!\!\!\mathrm{d}S = E(r)S = 4\pi r^2 E$

Hay que insistir, una y otra vez, que para que el campo se pueda extraer del flujo, debe primero transformarse esta integral en una de una cantidad escalar (normalmente el módulo del campo) y que esta cantidad es constante sobre los superficie de integración. Si no, no se puede extraer el campo y el flujo no es igual a 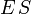$E\,S$ .

La ley de Gauss siempre es cierta, pero no siempre es útil

Igualando ahora la expresión del flujo a la carga encerrada dividida por $\varepsilon_0$ queda

$4\pi r^2 E = \frac{1}{\varepsilon_0}\begin{cases}0 & (r < R) \\ Q & (r>R)\end{cases}$

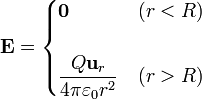
y la expresión para el campo, en forma vectorial, es $\mathbf{E} = \begin{cases}\mathbf{0} & (r < R) \\ & \\ \displaystyle \frac{Q\mathbf{u}_r}{4\pi\varepsilon_0 r^2} & (r > R)\end{cases}$

Expresado en palabras: el campo eléctrico creado por una esfera cargada uniformemente es nulo en el interior de la esfera, e igual al de una carga puntual en el exterior de ella. Esta carga puntual valdría el total de la carga de la esfera y estaría situada en el centro de ella.

3 Por integración directa

Ahora resolveremos este mismo problema por integración directa, esto es, partiendo de la expresión integral para el campo producido por una distribución de carga superficial

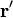$\mathbf{E}(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\int \sigma_s\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}S'$

En nuestro caso $\mathbf{r}$ representa un punto cualquiera del espacio, mientras que $\mathbf{r}'$ describe a los puntos de la superficie esférica.

La densidad de carga, si ésta está distribuida uniformemente, será

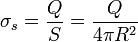
$\sigma_s = \frac{Q}{S}=\frac{Q}{4\pi R^2}$

Podemos elegir el sistema de ejes de tal forma que el eje $Z$ coincida con la línea que pasa por el centro de la esfera y el punto de observación $\mathbf{r}$ , estando el origen de coordenadas en el centro de la esfera. De esta forma

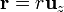
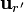$\mathbf{r}=r\mathbf{u}_z$ $\mathbf{r}'=R\mathbf{u}_{r'}$

Siendo $\mathbf{u}_{r'}$ un vector unitario radial, que habrá que pasar a la base cartesiana a la hora de integrar.

El vector de posición relativo y su módulo valen

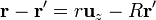
$\mathbf{r}-\mathbf{r}' = r \mathbf{u}_z - R \mathbf{r}'$ $|\mathbf{r}-\mathbf{r}'| =\sqrt{ (r \mathbf{u}_z - R \mathbf{r}')\cdot(r \mathbf{u}_z - R \mathbf{r}')} = \sqrt{r^2+R^2-2rR\cos\theta'}$

ya que 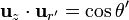$\mathbf{u}_z\cdot\mathbf{u}_{r'} = \cos\theta'$ , por definición del angulo $θ'$ (el que forma la dirección radial con el eje Z).

El diferencial de superficie, por último, es el correspondiente a una superficie $r$ constante

$\mathrm{d}S' = R^2\,\mathrm{sen}\,\theta'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'$

Al sustituir en la expresión integral para el campo, debemos pasar el integrando a la base cartesiana. El campo tendrá en principio tres componentes: $x$ , $y$ y $z$ . Sin ambargo, vista desde el punto de observación, la esfera cargada puede verse como compuesta de anillos cuyo eje pasa por este punto. Cada uno de los anillos, según se ve en otro problema, produce un campo en su eje que va en la dirección de dicho eje. Por tanto el campo en 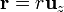$\mathbf{r}=r\mathbf{u}_z$ va a tener sólo componente en la dirección de $\mathbf{u}_z$ , por lo que no precisamos escribir las tres componentes, sino solo la tercera:

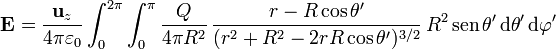
$\mathbf{E}= \frac{\mathbf{u}_z}{4\pi\varepsilon_0}\int_0^{2\pi}\int_0^{\pi}\frac{Q}{4\pi R^2}\,\frac{r-R\cos\theta'}{(r^2+R^2-2rR\cos\theta')^{3/2}}\,R^2\,\mathrm{sen}\,\theta'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'$

La integral en $\varphi$ nos da un factor $2π$ , ya que el integrando posee simetría acimutal. Nos queda entonces

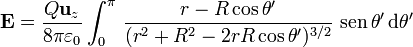
$\mathbf{E}= \frac{Q\mathbf{u}_z}{8\pi\varepsilon_0}\int_0^{\pi}\,\frac{r-R\cos\theta'}{(r^2+R^2-2rR\cos\theta')^{3/2}}\,\,\mathrm{sen}\,\theta'\,\mathrm{d}\theta'$

Para calcular esta integral en $θ'$ , hacemos el cambio de variable

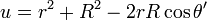
$u = r^2+R^2-2rR\cos\theta'\,$ $u(\theta'=0) = (r-R)^2\,$ $u(\theta'=\pi)=(r+R)^2\,$ $\mathrm{d}u = 2Rr\,\mathrm{sen}\,\theta'\,\mathrm{d}\theta'$

y queda

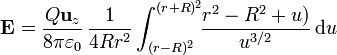
$\mathbf{E}= \frac{Q\mathbf{u}_z}{8\pi\varepsilon_0}\,\frac{1}{4Rr^2}\int_{(r-R)^2}^{(r+R)^2}\!\!\frac{r^2-R^2+u)}{u^{3/2}}\,\mathrm{d}u$

Separando la integral en dos

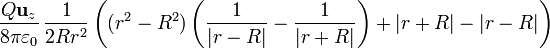
$\mathbf{E}= \frac{Q\mathbf{u}_z}{8\pi\varepsilon_0}\,\frac{1}{4Rr^2}\left((r^2-R^2)\int_{(r-R)^2}^{(r+R)^2}\!\!\frac{1}{u^{3/2}}\,\mathrm{d}u+\int_{(r-R)^2}^{(r+R)^2}\!\!\frac{1}{u^{1/2}}\,\mathrm{d}u\right) =$ $\frac{Q\mathbf{u}_z}{8\pi\varepsilon_0}\,\frac{1}{4Rr^2}\left[(r^2-R^2)\left(-\frac{2}{\sqrt{u}}\right)+2\sqrt{u}\right]_{(r-R)^2}^{(R+r)^2} =$ $\frac{Q\mathbf{u}_z}{8\pi\varepsilon_0}\,\frac{1}{2Rr^2}\left((r^2-R^2)\left(\frac{1}{|r-R|}-\frac{1}{|r+R|}\right)+|r+R|-|r-R|\right)$

En el resultado anterior, hay que tener mucho cuidado con que

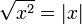
$\sqrt{x^2} = |x|\,$

Tenemos que, puesto que los dos radios son positivos

$|r+R| = r+R\,$

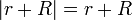
pero

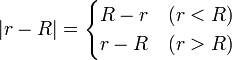
$|r-R| = \begin{cases}R-r & (r<R) \\ r-R & (r>R)\end{cases}$

Por ello distinguimos dos regiones en el resultado:

$r > R$ En el exterior de la esfera

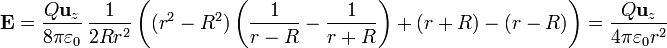
$\mathbf{E} = \frac{Q\mathbf{u}_z}{8\pi\varepsilon_0}\,\frac{1}{2Rr^2}\left((r^2-R^2)\left(\frac{1}{r-R}-\frac{1}{r+R}\right)+(r+R)-(r-R)\right) = \frac{Q\mathbf{u}_z}{4\pi\varepsilon_0 r^2}$

que es el campo de una carga puntual.

$r < R$ En el interior de la esfera

$\mathbf{E} = \frac{Q\mathbf{u}_z}{8\pi\varepsilon_0}\,\frac{1}{2Rr^2}\left((r^2-R^2)\left(\frac{1}{R-r}-\frac{1}{r+R}\right)+(r+R)-(R-r)\right) = \mathbf{0}$

que es un campo nulo.

Queda un último paso antes de escribir la expresión del campo eléctrico. Hemos fijado el eje $Z$ en la dirección del punto de observación. Pero, ¿qué ocurre si tenemos dos puntos diferentes en los que queremos hallar el campo y cuyos valores queremos comparara? No puede ser que el eje $Z$ apunte en la dirección de ambos puntos a la vez.

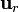La solución es recuperar la interpretación geométrica. En este problema $\mathbf{u}_z$ es el unitario que apunta en la dirección y sentido que va del centro de la esfera al punto de observación $\mathbf{r}$ . Pero ésta no es más que la definición general de $\mathbf{u}_r$ . Por tanto, la expresión del campo para cualquier punto del espacio es

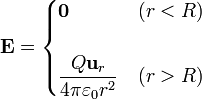
$\mathbf{E} = \begin{cases}\mathbf{0} & (r < R) \\ & \\ \displaystyle \frac{Q\mathbf{u}_r}{4\pi\varepsilon_0 r^2} & (r > R)\end{cases}$

Puede resultar extraño que el campo en el interior de la esfera cargada sea nulo. Es evidente que en el centro de la esfera debe serlo, por simetría. El resultado, no obstante, es más fuerte. El campo es nulo en todos los puntos del interior de la esfera. Parece antiintuitivo que, si uno carga negativa se acerca a la superficie (cargada positivamente) por la parte de dentro, no experimente una fuerza de atracción debida a las cargas de la superficie que están cerca de ella. Esta atracción, por supuesto, existe, pero se ve compensada por la atracción debida al resto de cargas de la superficie esférica, que tiran en sentido opuesto. Ese resto de cargas están más alejadas, pero son mayoría, por lo que finalmente ambos efectos se compensan y la fuerza es nula.
Este efecto también es aplicable al campo gravitatorio, pues la ley de Newton es análoga a la ley de Coulomb. Ello quiere decir que, en un planeta hueco, sus habitantes subterráneos no caminarían por la cara interior del planeta, sino que flotarían ingrávidos en el interior

Campo debido a una superficie esférica cargada

De Laplace

Contenido

1 Enunciado

2 Aplicando las leyes de la electrostática

3 Por integración directa

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES