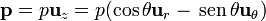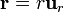Campo de dos anillos coaxiales

De Laplace

Contenido

1 Enunciado
2 Potencial
3 Campo eléctrico, fuerza y trabajo
4 Fuerza y energía de un dipolo
- 4.1 Fuerza sobre el dipolo
- 4.2 Energía potencial
5 Desarrollo multipolar

1 Enunciado

Dos anillos iguales de radio

R

y grosor despreciable están cargados eléctricamente con sendas distribuciones lineales y uniformes

+ λ 0

y

- λ 0

. Los anillos se encuentran en planos paralelos separados una distancia

R

, pero con sus centros situados sobre el mismo eje. Tómese este eje como

Z

, y como origen de coordenadas

O

el punto medio entre los anillos.

Obtenga la expresión del potencial electrostático creado por estas distribuciones en los puntos del eje $Z$ . Calcule el valor del potencial en un punto arbitrario del plano $X Y$ .
Obtenga la expresión del campo eléctrico para los puntos del eje $Z$ . ¿Cuánto vale la fuerza que actúa sobre una carga puntual $q$ situada en O? ¿Qué trabajo se ha realizado para traer esta carga desde el infinito hasta este punto?
Suponga que, en lugar de la carga puntual, se sitúa un dipolo eléctrico de momento dipolar 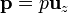$\mathbf{p}=p\mathbf{u}_z$ , en el centro del anillo de carga positiva. Obtenga la expresión de la energía potencial del dipolo y la fuerza que actúa sobre él.
Obtenga los momentos monopolar y dipolar del sistema de dos anillos y proporcione expresiones aproximadas para el potencial eléctrico y el campo eléctrico en puntos alejados del sistema

2 Potencial

Tanto el potencial eléctrico como el campo de dos anillos pueden calcularse mediante el principio de superposición, hallando en primer lugar el potencial de un solo anillo y posteriormente sumando las dos contribuciones.

2.1 Campo de un solo anillo

Consideremos el anillo en $z = + R / 2$ . El potencial que produce en su eje puede hallarse por integración directa, según la expresión

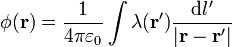
$\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \lambda(\mathbf{r}')\frac{\mathrm{d}l'}{|\mathbf{r}-\mathbf{r}'|}$

Tenemos que

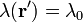
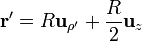
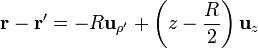
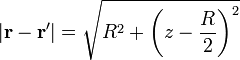
$\lambda(\mathbf{r}')=\lambda_0$ $\mathbf{r}=z\mathbf{u}_z\,$ $\mathbf{r}'=R\mathbf{u}_{\rho'}+\frac{R}{2}\mathbf{u}_z\,$ $\mathbf{r}-\mathbf{r}'=-R\mathbf{u}_{\rho'}+\left(z-\frac{R}{2}\right)\mathbf{u}_z\,$ $|\mathbf{r}-\mathbf{r}'|=\sqrt{R^2+\left(z-\frac{R}{2}\right)^2}$ $\mathrm{d}l'=|\mathrm{d}\mathbf{r}'|=R\,\mathrm{d}\varphi'$

Sustituyendo todo esto queda la integral

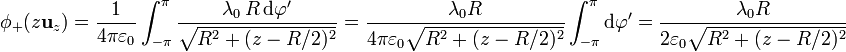
$\phi_+(z\mathbf{u}_z)=\frac{1}{4\pi\varepsilon_0}\int_{-\pi}^\pi \frac{\lambda_0\,R\,\mathrm{d}\varphi'}{\sqrt{R^2+(z-R/2)^2}} = \frac{\lambda_0 R}{4\pi\varepsilon_0\sqrt{R^2+(z-R/2)^2}}\int_{-\pi}^\pi \mathrm{d}\varphi'=\frac{\lambda_0 R}{2\varepsilon_0\sqrt{R^2+(z-R/2)^2}}$

2.2 Potencial de los dos anillos

El potencial del segundo anillo es análogo al anterior, sin más que cambiar

+ λ 0

por

- λ 0

y

+ R / 2

por

- R / 2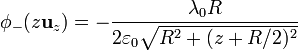

$\phi_-(z\mathbf{u}_z)=-\frac{\lambda_0 R}{2\varepsilon_0\sqrt{R^2+(z+R/2)^2}}$

Sumando las dos contribuciones

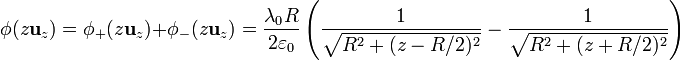
$\phi(z\mathbf{u}_z)=\phi_+(z\mathbf{u}_z)+\phi_-(z\mathbf{u}_z)=\frac{\lambda_0R}{2\varepsilon_0}\left(\frac{1}{\sqrt{R^2+(z-R/2)^2}}-\frac{1}{\sqrt{R^2+(z+R/2)^2}}\right)$

2.3 Potencial en el plano XY

En los puntos del plano XY, equidistante de los dos anillos, el potencial de cada anillo posee una expresión extremadamente complicada que requiere matemáticas avanzadas. Sin embargo, no se nos pide el potencial de cada anillo por separado, sino del sistema de dos anillos y este es trivial: vale cero.

Para verlo, consideremos dos elementos de carga, uno por cada anillo, situados simétricamente respecto al plano XY. Estos dos elementos tendrán cargas iguales y opuestas , 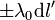$\pm\lambda_0\mathrm{d}l'$ . Todos los puntos del plano XY se encuentran a la misma distancia de estos dos elementos, 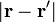$|\mathbf{r}-\mathbf{r}'|$ , y por ello, sus contribuciones al potencial total se van a cancelar mutuamente

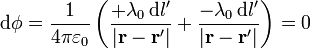
$\mathrm{d}\phi = \frac{1}{4\pi\varepsilon_0}\left(\frac{+\lambda_0\,\mathrm{d}l'}{|\mathbf{r}-\mathbf{r}'|}+\frac{-\lambda_0\,\mathrm{d}l'}{|\mathbf{r}-\mathbf{r}'|}\right) = 0$

Puesto que esto es cierto para cada elemento de carga que tomemos, y para cualquier punto del plano XY, el potencial total en todos los puntos del plano XY es nulo.

3 Campo eléctrico, fuerza y trabajo

3.1 Campo eléctrico

El campo eléctrico en el eje se calcula, al igual que el potencial, mediante el principio de superposición. Primero se calcula el campo eléctrico de un solo anillo, como ya se hace en otro problema) y luego se suma el del segundo anillo.

Para el caso de un solo anillo, el cálculo es idéntico al del caso de un anillo en el plano XY, simplemente trasladando la posición del centro del anillo.

La expresión general para el campo creado por una distribución lineal de carga es

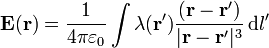
$\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \lambda(\mathbf{r}')\frac{ (\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}l'$

Tenemos que, como antes,

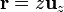
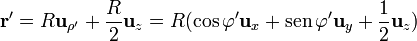
$\mathbf{r}=z\mathbf{u}_{z}$ $\mathbf{r}'=R\mathbf{u}_{\rho'}+\frac{R}{2}\mathbf{u}_z=R(\cos\varphi'\mathbf{u}_{x}+\mathrm{sen}\,\varphi'\mathbf{u}_{y}+\frac{1}{2}\mathbf{u}_z)$

$\mathrm{d}l'=|\mathrm{d}\mathbf{r}'|=R\,\mathrm{d}\varphi'$ $\mathbf{r}-\mathbf{r}'=-R\cos\varphi'\mathbf{u}_{x}-R\,\mathrm{sen}\,\varphi'\mathbf{u}_{y}+\left(z-\frac{R}{2}\right)\mathbf{u}_{z}$

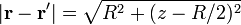
$|\mathbf{r}-\mathbf{r}'|=\sqrt{R^2+(z-R/2)^2}$

Al sustituir e integrar, las componentes $x$ e $y$ del campo se anulan, por la simetría de la distribución, o bien aplicando que la integral en un periodo de 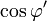$\cos\varphi'$ y de $\mathrm{sen}\,\varphi'$ es nula. Para la componente z tenemos

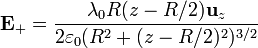
$\mathbf{E}_+=\frac{\lambda_0R(z-R/2)\mathbf{u}_z}{2\varepsilon_0(R^2+(z-R/2)^2)^{3/2}}$

Sumando ahora la contribución del anillo de carga negativa situada en $z = - R / 2$ queda el campo total en el eje

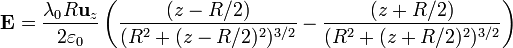
$\mathbf{E}=\frac{\lambda_0R\mathbf{u}_z}{2\varepsilon_0}\left(\frac{(z-R/2)}{(R^2+(z-R/2)^2)^{3/2}}-\frac{(z+R/2)}{(R^2+(z+R/2)^2)^{3/2}}\right)$

3.2 Fuerza sobre una carga puntual

Si situamos una carga puntual en el origen de coordenadas, la fuerza sobre esta carga es

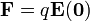
$\mathbf{F}=q\mathbf{E}(\mathbf{0})$

Haciendo $z = 0$ en la expresión del campo

$\mathbf{F}=\frac{q\lambda_0R\mathbf{u}_z}{2\varepsilon_0}\left(\frac{-R/2}{\left(R^2+(R/2)^2\right)^{3/2}}-\frac{R/2}{\left(R^2+(R/2)^2\right)^{3/2}}\right) = -\frac{4q\lambda_0\mathbf{u}_z}{5\sqrt{5}\varepsilon_0 R}$

Si la carga es positiva, esta fuerza va hacia abajo, como corresponde a que el campo vaya de las cargas positivas a las negativas.

3.3 Trabajo para traer la carga

El trabajo necesario para traer la carga desde el infinito es igual al producto de la carga por la diferencia de potencial

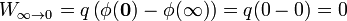
$W_{\infty\to 0}=q\left(\phi(\mathbf{0})-\phi(\infty)\right)=q(0-0) = 0$

Este trabajo es nulo pues va de un punto a otro situado al mismo potencial.

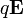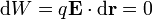Podemos verlo de otra forma imaginando que traemos la carga por un camino situado en todo momento en el plano XY. Al moverse en todo instante por una equipotencial no se realiza trabajo sobre la carga: la fuerza $q\mathbf{E}$ es perpendicular a la equipotencial y por tanto al desplazamiento, $\mathrm{d}W=q\mathbf{E}\cdot\mathrm{d}\mathbf{r}=0$ .

4 Fuerza y energía de un dipolo

4.1 Fuerza sobre el dipolo

Un dipolo alineado según el eje Z, 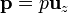$\mathbf{p}=p\mathbf{u}_z$ , experimenta una fuerza

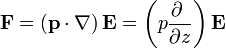
$\mathbf{F}=\left(\mathbf{p}\cdot\nabla\right)\mathbf{E}=\left(p\frac{\partial\ }{\partial z}\right)\mathbf{E}$

En este caso conocemos el campo sólo en los puntos del eje Z y por tanto no sabemos cómo depende de $x$ o $y$ (ya que lo hemos calculado sólo para $x = y = 0$ ). Sin embargo, puesto que la fuerza sólo requiere una derivada en z y sí conocemos la dependencia en esta coordenada, podemos hallar esta fuerza derivando la expresión calculada previamente. Eso sí, no podemos sustituir la posición del dipolo $z = R / 2$ hasta después de haber calculado dicha derivada.

Para simplificar las expresiones, primero calcularemos la fuerza cada anillo produce sobre el dipolo y luego sumaremos las dos contribuciones.

Derivando 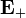$\mathbf{E}_+$ obtenemos

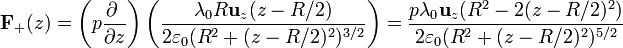
$\mathbf{F}_+(z)=\left(p\frac{\partial\ }{\partial z}\right)\left(\frac{\lambda_0R\mathbf{u}_z(z-R/2)}{2\varepsilon_0(R^2+(z-R/2)^2)^{3/2}}\right) = \frac{p\lambda_0\mathbf{u}_z(R^2-2(z-R/2)^2)}{2\varepsilon_0(R^2+(z-R/2)^2)^{5/2}}$

que en $z = R / 2$ vale

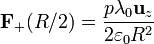
$\mathbf{F}_+(R/2)= \frac{p\lambda_0\mathbf{u}_z}{2\varepsilon_0R^2}$

Operando del mismo modo para el anillo de carga negativa

$\mathbf{F}_-(z)=\left(p\frac{\partial\ }{\partial z}\right)\left(\frac{-\lambda_0R\mathbf{u}_z(z+R/2)}{2\varepsilon_0(R^2+(z+R/2)^2)^{3/2}}\right) = -\frac{p\lambda_0R\mathbf{u}_z(R^2-2(z+R/2)^2)}{2\varepsilon_0(R^2+(z+R/2)^2)^{5/2}}$

que en $z = R / 2$ vale

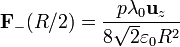
$\mathbf{F}_-(R/2)= \frac{p\lambda_0\mathbf{u}_z}{8\sqrt{2}\varepsilon_0R^2}$

Sumando los dos términos

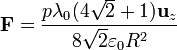
$\mathbf{F}=\frac{p\lambda_0(4\sqrt{2}+1)\mathbf{u}_z}{8\sqrt{2}\varepsilon_0R^2}$

4.2 Energía potencial

La energía potencial electrostática del dipolo es más sencilla de calcular, ya que solo necesitamos el valor del campo en la posición del dipolo:

$U_\mathrm{e}=-\mathbf{p}\cdot\mathbf{E}(R/2)=-\left(p\mathbf{u}_z\right)\cdot\left.\left(\frac{\lambda_0\mathbf{u}_z}{2\varepsilon_0}\left(\frac{z-R/2}{(R^2+(z-R/2)^2)^{3/2}}-\frac{z+R/2}{(R^2+(z+R/2)^2)^{3/2}}\right)\right)\right|_{z=R/2}=\frac{p\lambda_0}{4\sqrt{2}\varepsilon_0R^2}$

5 Desarrollo multipolar

Los dos primeros momentos multipolares son la carga y el momento dipolar de la distribución:

Carga: La carga neta del sistema es nula, ya que la positiva de un anillo se anula con la negativa del otro

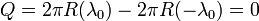
$Q = 2\pi R (\lambda_0)-2\pi R (-\lambda_0) = 0\,$

Momento dipolar: El momento dipolar no es nulo, ya que la distribución de cargas es claramente equivalente, para puntos alejados, a un dipolo que va de las cargas negativas a las positivas

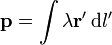
$\mathbf{p}=\int \lambda\mathbf{r}'\,\mathrm{d}l'$

Separando las dos contribuciones y aplicando la expresión de 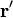$\mathbf{r}'$ que dimos antes, tenemos para el anillo positivo

$\mathbf{p}_+=\int_{-\pi}^\pi \lambda_0(R\cos\varphi'\mathbf{u}_x+R\,\mathrm{sen}\,\varphi'\mathbf{u}_y+(R/2)\mathbf{u}_z)\,R\,\mathrm{d}\varphi'=\pi\lambda_0R^2\mathbf{u}_z$

y para el negativo

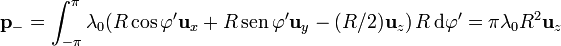
$\mathbf{p}_-=\int_{-\pi}^\pi \lambda_0(R\cos\varphi'\mathbf{u}_x+R\,\mathrm{sen}\,\varphi'\mathbf{u}_y-(R/2)\mathbf{u}_z)\,R\,\mathrm{d}\varphi'=\pi\lambda_0R^2\mathbf{u}_z$

y el momento dipolar total de la distribución es

$\mathbf{p}=\mathbf{p}_++\mathbf{p}_-=2\pi\lambda_0R^2\mathbf{u}_z\,$

Una vez que tenemos estos dos momentos podemos dar la expresión aproximada para el potencial eléctrico

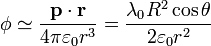
$\phi \simeq \frac{\mathbf{p}\cdot\mathbf{r}}{4\pi\varepsilon_0 r^3}=\frac{\lambda_0R^2 \cos\theta}{2\varepsilon_0 r^2}$

y para el campo eléctrico

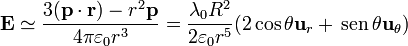
$\mathbf{E} \simeq \frac{3(\mathbf{p}\cdot\mathbf{r})-r^2\mathbf{p}}{4\pi\varepsilon_0 r^3}=\frac{\lambda_0R^2}{2\varepsilon_0 r^5}(2\cos\theta\mathbf{u}_r+\,\mathrm{sen}\,\theta\mathbf{u}_\theta)$

donde, para expresar el resultado en esféricas se ha aplicado que

$\mathbf{p}=p\mathbf{u}_z = p(\cos\theta\mathbf{u}_r-\,\mathrm{sen}\,\theta\mathbf{u}_\theta)$ $\mathbf{r}=r\mathbf{u}_r$

Campo de dos anillos coaxiales

De Laplace

Contenido

1 Enunciado

2 Potencial

2.1 Campo de un solo anillo

2.2 Potencial de los dos anillos

2.3 Potencial en el plano XY

3 Campo eléctrico, fuerza y trabajo

3.1 Campo eléctrico

3.2 Fuerza sobre una carga puntual

3.3 Trabajo para traer la carga

4 Fuerza y energía de un dipolo

4.1 Fuerza sobre el dipolo

4.2 Energía potencial

5 Desarrollo multipolar

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES