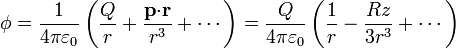Campo eléctrico de una esfera horadada
De Laplace
Contenido |
1 Enunciado
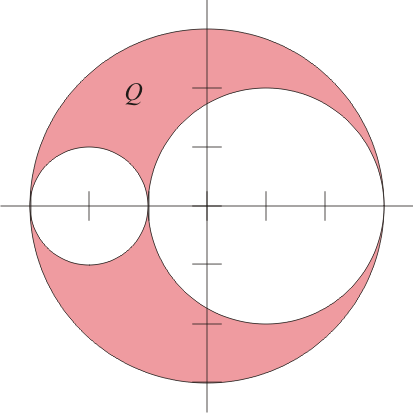
En un volumen en forma de esfera (de radio 3R) en la que se han hecho dos huecos (también esféricos, uno de radio 2R y otro de radio R) se distribuye uniformemente una carga Q.- Calcule el campo eléctrico en el punto P, de tangencia de los dos huecos.
- Halle el potencial eléctrico en el mismo punto P.
- Calcule los dos primeros momentos multipolares del sistema, tomando como origen de coordenadas el centro de la esfera grande.
2 Solución
2.1 Campo eléctrico en P
En este apartado se trata de hallar el campo eléctrico en el punto P, no en todo el espacio.
Para ello, aplicaremos el principio de superposición. Nuestra distribución en forma de esfera con dos huecos la podemos considerar como compuesta de una esfera maciza, de radio 3R y densidad de carga ρ0 (cuyo valor calcularemos a continuación), y dos esferas también macizas, de densidad de carga − ρ0 y de radios R y 2R, descentradas respecto a la esfera mayor.
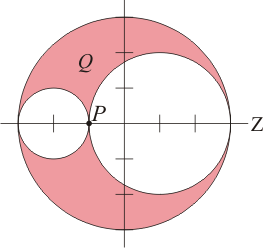 | = | |||
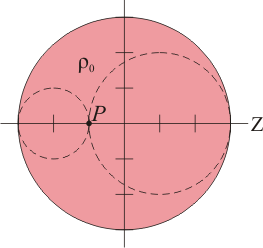 | + | 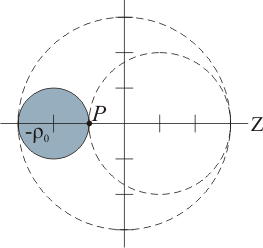 | + | 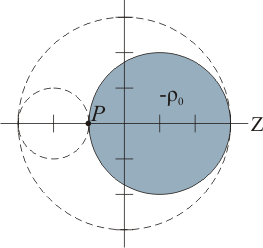
|
Calculamos en primer lugar el valor de ρ0 imponiendo que la carga total del sistema sea Q

Por tanto
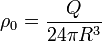
El sistema se compone entonces de tres esferas, de cargas totales
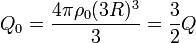
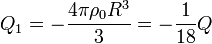
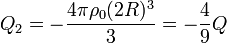
estando los centros respectivos en
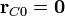

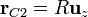
donde hemos tomado el origen de coordenadas en el centro de la esfera grande y el eje Z el que pasa por los tres centros.
Ahora se trata de sumar los campos correspondientes a cada una de las esferas. En cada caso podemos aplicar la expresión para el campo de una esfera de radio a cargada uniformemente con una carga Q:
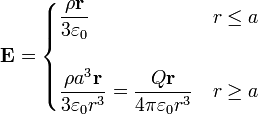
Físicamente esta fórmula quiere decir que el campo debido a una esfera cargada uniformemente en el volumen equivale al de una carga puntual situada en su centro, para los puntos del exterior, y varía linealmente, para los puntos del interior.
Esta expresión presupone que el origen de coordenadas se encuentra en el centro de la esfera. Si no es así, sino que se encuentra centra en 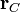 simplemente se traslada, sustituyendo
simplemente se traslada, sustituyendo  por
por 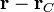 .
.
En nuestro caso, el punto P se encuentra en el interior de la esfera grande y en la frontera de los dos huecos. Usando el sistema de ejes indicado anteriormente, la posición del punto P es
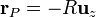
de forma que el campo debido a la esfera mayor es
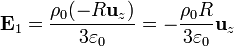
Para los dos huecos podemos usar tanto la expresión interior como la exterior, por encontrarse el punto P en la frontera.
Para el hueco pequeño, centrado en 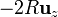 el campo es
el campo es
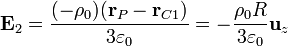
Para el hueco grande, centrado en 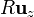 , el campo es
, el campo es
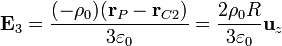
de forma que el campo total en P es
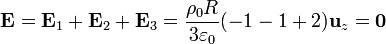
esto es, es nulo, independientemente del valor de ρ0 y de Q.
Si se quiere emplear el campo de cargas puntuales para los dos huecos el resultado es, naturalmente, el mismo
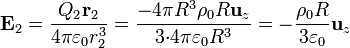
siendo  el vector de posición relativo al centro del hueco pequeño. Del mismo modo
el vector de posición relativo al centro del hueco pequeño. Del mismo modo
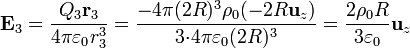
resultando un campo total nulo.
2.2 Potencial eléctrico en P
El cálculo del potencial eléctrico es en la misma línea que el anterior, aunque requiere un poco de cálculo adicional.
De nuevo aplicamos el principio de superposición, sumando el potencial de una esfera maciza con densidad de carga ρ0 y dos esferas, también macizas, de densidad − ρ0.
Para el potencial debido a los dos huecos el cálculo es simple: Una esfera cargada uniformemente produce en su exterior el mismo potencial que una carga puntual situada en su centro. Por tanto
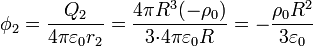
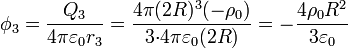
Para la esfera grande, debemos calcular el potencial dentro de una esfera maciza. Esto lo podemos hacer integrando la expresión del campo eléctrico
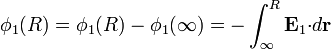
Esta integral se compone de dos tramos, uno desde el infinito hasta la superficie de la esfera y otro desde ahí hasta el punto final, situado a una distancia R del centro. En cada uno de estos tramos hay que emplear la expresión del campo eléctrico correspondiente.
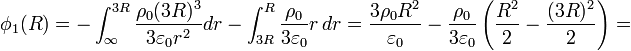
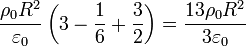
A esta expresión se puede llegar directamente si se conoce la expresión para el potencial en el interior de una esfera maciza cargada
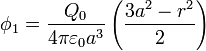
Sustituyendo Q0 por 4π(3R)3ρ0 / 3, a por 3R y r por R queda finalmente
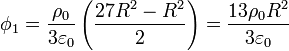
Sumando las tres contribuciones tenemos el potencial en el punto $P$
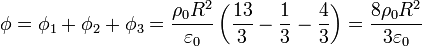
Sustituyendo ahora el valor de ρ0 queda finalmente
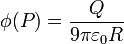
2.3 Momentos multipolares del sistema
Los dos primeros momentos multipolares son la carga total y el momento dipolar total.
La carga ya la conocemos. No es otra que Q
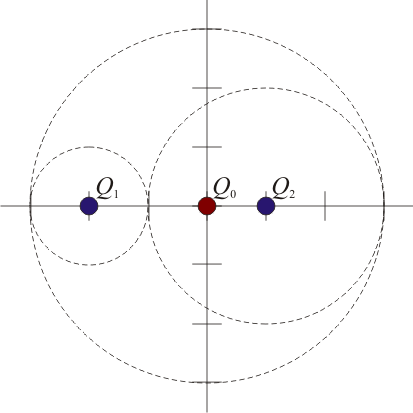
Para el momento dipolar observamos que, desde fuera, el sistema se ve como tres cargas puntuales, una positiva situada en el centro de la esfera grande y sendas cargas negativas situadas en los centros de los huecos.
 | ≡ | 
|
Por tanto el momento dipolar es
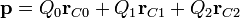
Sustituyendo cada término
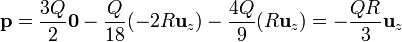
El potencial en puntos alejados será entonces, aproximadamente