Potencial eléctrico de un segmento cargado

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Sea un segmento rectilíneo de longitud $L$ , sobre el cual existe una densidad de carga uniforme $λ$ .

Halle el potencial que produce en un punto cualquiera del espacio.
Demuestre que las equipotenciales son elipsoides con focos los extremos del segmento.

2 Solución

2.1 Potencial eléctrico

El cálculo del potencial eléctrico debido a un segmento es algo más complicado que el del campo eléctrico, pese a que la integral es aparentemente más simple. Para hallar el potencial por integración directa, debemos resolver la integral

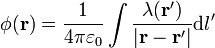
$\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \frac{\lambda(\mathbf{r'})}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}l'$

En nuestro caso, empleando los mismos ejes y las mismas variables que para el cálculo del campo eléctrico, nos queda

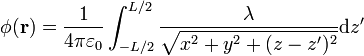
$\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int_{-L/2}^{L/2} \frac{\lambda}{\sqrt{x^2+y^2+(z-z')^2}}\mathrm{d}z'$

Empleando de nuevo el cambio de variable

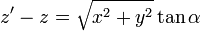
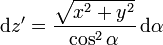
$z'-z=\sqrt{x^2+y^2}\tan\alpha$ $\mathrm{d}z'=\frac{\sqrt{x^2+y^2}}{\cos^2\alpha}\,\mathrm{d}\alpha$

nos queda ahora

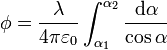
$\phi= \frac{\lambda}{4\pi\varepsilon_0}\int_{\alpha_1}^{\alpha_2}\frac{\mathrm{d}\alpha}{\cos\alpha}$

Esta integral no es inmediata, pero existen técnicas “mecánicas” para resolverla. Una posibilidad es introducir el nuevo cambio de variable

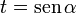
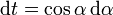
$t = \mathrm{sen}\,\alpha$ $\mathrm{d}t = \cos\alpha\,\mathrm{d}\alpha$

y la integral se nos transforma en

$\phi = \frac{\lambda}{4\pi\varepsilon_0}\int_{t_1}^{t_2}\frac{\mathrm{d}t}{1-t^2}$

Esta integral se descompone en dos fracciones y obtenemos finalmente

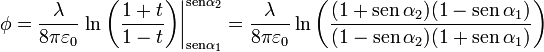
$\phi = \frac{\lambda}{8\pi\varepsilon_0}\left.\ln\left(\frac{1+t}{1-t}\right)\right|_{\mathrm{sen}\alpha_1}^{\mathrm{sen}\alpha_2} = \frac{\lambda}{8\pi\varepsilon_0}\ln\left(\frac{(1+\mathrm{sen}\,\alpha_2)(1-\mathrm{sen}\,\alpha_1)}{(1-\mathrm{sen}\,\alpha_2)(1+\mathrm{sen}\,\alpha_1)}\right)$

Una forma alternativa y mucho más directa consiste en emplear funciones hiperbólicas. Si en lugar del cambio de variable de la tangente, empleamos

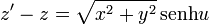
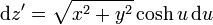
$z'-z=\sqrt{x^2+y^2}\,\mathrm{senh}u$ $\mathrm{d}z'=\sqrt{x^2+y^2}\cosh u\,\mathrm{d}u$

nos queda, simplemente,

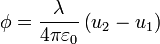
$\phi = \frac{\lambda}{4\pi\varepsilon_0}\left(u_2-u_1\right)$

o, en términos de las dimensiones del segmento,

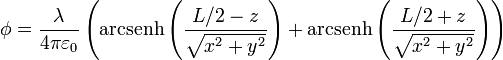
$\phi = \frac{\lambda}{4\pi\varepsilon_0}\left(\mathrm{arcsenh}\left(\frac{L/2-z}{\sqrt{x^2+y^2}}\right)+\mathrm{arcsenh}\left(\frac{L/2+z}{\sqrt{x^2+y^2}}\right)\right)$

2.2 Superficies equipotenciales

Se trata de ver que la fea ecuación,

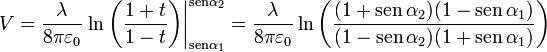
$V = \frac{\lambda}{8\pi\varepsilon_0}\left.\ln\left(\frac{1+t}{1-t}\right)\right|_{\mathrm{sen}\alpha_1}^{\mathrm{sen}\alpha_2} = \frac{\lambda}{8\pi\varepsilon_0}\ln\left(\frac{(1+\mathrm{sen}\,\alpha_2)(1-\mathrm{sen}\,\alpha_1)}{(1-\mathrm{sen}\,\alpha_2)(1+\mathrm{sen}\,\alpha_1)}\right)$

o, alternativamente

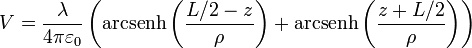
$V = \frac{\lambda}{4\pi\varepsilon_0}\left(\mathrm{arcsenh}\left(\frac{L/2-z}{\rho}\right)+\mathrm{arcsenh}\left(\frac{z+L/2}{\rho}\right)\right)$

para un $V$ fijo, es la de un elipsoide en torno al segmento

Antes de hacer el cálculo veamos que este resultado es razonable. Para el caso de una carga puntual tenemos equipotenciales esféricas. Para un segmento obtenido estirando una carga a lo largo de una línea, las superficies equipotenciales, que envuelven a la carga, deberían ser al menos superficies parecidas a elipsoides.

La demostración de este resultado es bastante laboriosa. Aquí tenemos dos demostraciones alternativas. Una puramente analítica. La otra, con un mayor significado geométrico.

2.2.1 Demostración geométrica

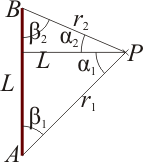
Consideremos el triángulo ABP formado por los extremos del segmento (A y B) y el punto de observación P. Supondremos, para simplificar el cálculo, que este punto P se encuentra a una altura intermedia entre los dos extremos (aunque no necesariamente en el plano central). Los lados de este triángulo valen

L

,

r 1

y

r 2

, siendo estas dos últimas cantidades las distancias a los extremos inferior y superior, respectivamente.

Vamos a demostrar que

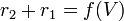
$r_2 + r_1 = f(V)\,$

esto es, que la suma de las distancias a los extremos es una constante para cada superficie equipotencial. Si demostramos esto, habremos probado que estas superficies son elipsoides con focos en los extremos del segmento. Partiremos de la expresión para el potencial

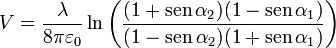
$V = \frac{\lambda}{8\pi\varepsilon_0}\ln\left(\frac{(1+\mathrm{sen}\,\alpha_2)(1-\mathrm{sen}\,\alpha_1)}{(1-\mathrm{sen}\,\alpha_2)(1+\mathrm{sen}\,\alpha_1)}\right)$

En términos del triángulo ABP, los ángulos $- α 1$ y $α 2$ son los que forma la altura por P con los lados AP y BP. Estos ángulos pueden relacionarse con los ángulos $β 1$ y $β 2$ que estos lados forman con el segmento AB.

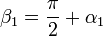
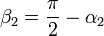
$\beta_1 = \frac{\pi}{2}+\alpha_1$ $\beta_2=\frac{\pi}{2}-\alpha_2$

y la ecuación para las equipotenciales se convierte en

$V = \frac{\lambda}{8\pi\varepsilon_0}\ln\left(\frac{(1+\cos\beta_2)(1+\cos\beta_1)}{(1-\cos\beta_2)(1-\cos\beta_1)}\right)$

Ahora bien, por el teorema del coseno

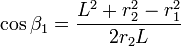
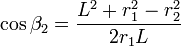
$\cos\beta_1 = \frac{L^2+r_2^2-r_1^2}{2r_2L}$ $\cos\beta_2 = \frac{L^2+r_1^2-r_2^2}{2r_1L}$

y de aquí

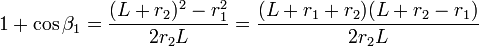
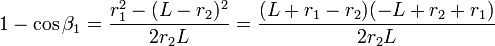
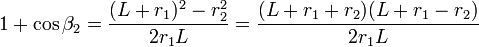
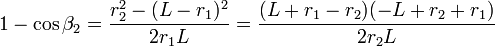
$1+\cos\beta_1 = \frac{(L+r_2)^2-r_1^2}{2r_2L}=\frac{(L+r_1+r_2)(L+r_2-r_1)}{2r_2L}$ $1-\cos\beta_1 = \frac{r_1^2-(L-r_2)^2}{2r_2L}=\frac{(L+r_1-r_2)(-L+r_2+r_1)}{2r_2L}$ $1+\cos\beta_2 = \frac{(L+r_1)^2-r_2^2}{2r_1L}=\frac{(L+r_1+r_2)(L+r_1-r_2)}{2r_1L}$ $1-\cos\beta_2 = \frac{r_2^2-(L-r_1)^2}{2r_1L}=\frac{(L+r_1-r_2)(-L+r_2+r_1)}{2r_2L}$

Sustituyendo esto en la ecuación de las equipotenciales

$V = \frac{\lambda}{8\pi\varepsilon_0}\ln\left(\frac{(L+r_1+r_2)(L+r_2-r_1)(L+r_1+r_2)(L+r_1-r_2)}{(L+r_1-r_2)(-L+r_2+r_1)(L+r_1-r_2)(-L+r_2+r_1)}\right) = \frac{\lambda}{4\pi\varepsilon_0}\ln\left(\frac{L+r_1+r_2}{-L+r_2+r_1}\right)$

y ya casi está, pues de aquí podemos despejar $r 1 + r 2$ . Hallando la exponencial

$\frac{L+r_1+r_2}{-L+r_2+r_1} = \exp\left(\frac{4\pi\varepsilon_0 V}{\lambda}\right)$

Multiplicando por 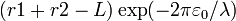$(r1+r2-L)\exp(-2\pi\varepsilon_0/\lambda)$ en ambos miembros

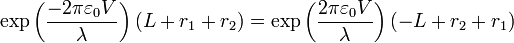
$\exp\left(\frac{-2\pi\varepsilon_0 V}{\lambda}\right)(L+r_1+r_2) = \exp\left(\frac{2\pi\varepsilon_0 V}{\lambda}\right)(-L+r_2+r_1)$

esto es

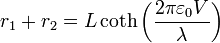
$r_1+r_2 = L \coth\left(\frac{2\pi\varepsilon_0 V}{\lambda}\right)$

dicho en palabras: la suma de las distancias a los extremos del segmento es constante para cada equipotencial. Por tanto las equipotenciales son elipsoides con focos en los extremos del segmento.

Elipsoides y no elipses porque estamos en tres dimensiones y el sistema posee simetrñia de revolución en torno al eje $Z$ . En particular, este tipo de elipsoides que poseen el semieje mayor en la dirección del eje de revolución se denominan elipsoides prolatos (los aplastados como tortas se denominan oblatos).

Podemos ver que si 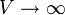$V\to\infty$ , como la cotangente hiperbólica tiende a la unidad, esto se convierte en

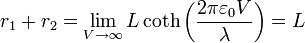
$r_1+r_2 = \lim_{V\to\infty}L \coth\left(\frac{2\pi\varepsilon_0 V}{\lambda}\right) = L$

lo cual quiere decir que la equipotencial se reduce al propio segmento.

Por contra, si 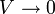$V\to 0$ ,

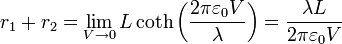
$r_1+r_2 = \lim_{V\to 0}L \coth\left(\frac{2\pi\varepsilon_0 V}{\lambda}\right) = \frac{\lambda L}{2\pi\varepsilon_0 V}$

esta distancia crece sin límites, y el elipsoide tiende a una esfera centrada en el segmento (que se ve como un punto desde muy lejos)

2.2.2 Demostración analítica

Partimos ahora de la expresión

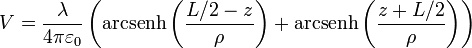
$V = \frac{\lambda}{4\pi\varepsilon_0}\left(\mathrm{arcsenh}\left(\frac{L/2-z}{\rho}\right)+\mathrm{arcsenh}\left(\frac{z+L/2}{\rho}\right)\right)$

Comenzamos despejando uno de los arcosenos hiperbólicos

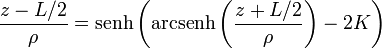
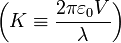
$\frac{z-L/2}{\rho} = \mathrm{senh}\left(\mathrm{arcsenh}\left(\frac{z+L/2}{\rho}\right)-2K\right)$ $\left(K \equiv \frac{2\pi\varepsilon_0V}{\lambda}\right)$

Desarrollando ahora el seno de la diferencia

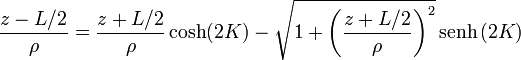
$\frac{z-L/2}{\rho} = \frac{z+L/2}{\rho}\cosh(2K)- \sqrt{1+\left(\frac{z+L/2}{\rho}\right)^2}\,\mathrm{senh}\,(2K)$

Despejando ahora la raíz y multiplicando por $ρ$ nos queda

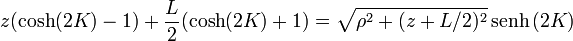
$z(\cosh(2K)-1) + \frac{L}{2}(\cosh(2K)+1)= \sqrt{\rho^2+(z+L/2)^2}\,\mathrm{senh}\,(2K)$

Aplicando las fórmulas del ángulo doble

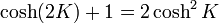
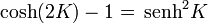
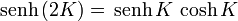
$\cosh(2K)+1 = 2\cosh^2K\,$ $\cosh(2K) - 1= \,\mathrm{senh}^2K\,$ $\mathrm{senh}\,(2K)= \,\mathrm{senh}\,K\,\cosh K\,$

obtenemos

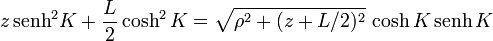
$z\,\mathrm{senh}^2K + \frac{L}{2}\cosh^2K = \sqrt{\rho^2+(z+L/2)^2}\,\cosh K\,\mathrm{senh}\,K$

Elevando al cuadrado y agrupando términos queda finalmente

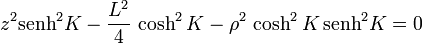
$z^2 \mathrm{senh}^2K- \frac{L^2}{4}\,\cosh^2K- \rho^2\,\cosh^2K\,\mathrm{senh}^2K= 0$

o, equivalentemente,

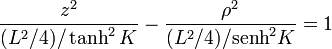
$\frac{z^2}{(L^2/4)/\tanh^2K}- \frac{\rho^2}{(L^2/4)/\mathrm{senh}^2K} = 1$

que es la ecuación de un elipsoide de revolución prolato. Los semiejes de este elipsoide valen,

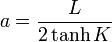
$a = \frac{L}{2\tanh K}$ $b = \frac{L}{2\,\mathrm{senh}\,K}$ $K = \frac{2\pi\varepsilon_0 V}{\lambda}$

La distancia del centro a cada foco es

$c = \sqrt{a^2-b^2} = \frac{L}{2}\sqrt{\frac{1}{\tanh^2K}-\frac{1}{\mathrm{senh}^2K}}= \frac{L}{2}$

esto es, todos los elipsoides tienen los focos en los extremos del segmento.

Si consideramos 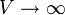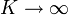$V\to\infty$ , $K\to\infty$ y los semiejes tienden a

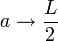
$a\to \frac{L}{2}$ $b\to 0$

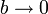
y el elipsoide se reduce al propio segmento.

Si en cambio V es muy pequeño los semiejes se comportan como

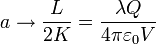
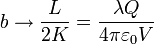
$a\to \frac{L}{2K} = \frac{\lambda Q}{4\pi\varepsilon_0 V}$ $b\to \frac{L}{2K} = \frac{\lambda Q}{4\pi\varepsilon_0 V}$

los semiejes tienen el mismo valor y el elipsoide se convierte en una esfera de radio tal que

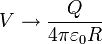
$V\to \frac{Q}{4\pi\varepsilon_0 R}$

como corresponde a una carga puntual.

2.3 Líneas de campo eléctrico

Una vez que sabemos que las superficies equipotenciales son elipsoides con focos en los extremos del segmento, podemos obtener las líneas de campo de forma inmediata, por las propiedades de las cónicas.

Las líneas de campo son hipérbolas que tienen sus focos en los extremos del segmento. Estas hipérbolas son ortogonales a los elipsoides equipotenciales.

Potencial eléctrico de un segmento cargado

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Potencial eléctrico

2.2 Superficies equipotenciales

2.2.1 Demostración geométrica

2.2.2 Demostración analítica

2.3 Líneas de campo eléctrico

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES