Sistema electrostático de tres cargas puntuales

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

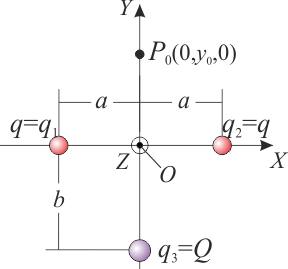
Un sistema electrostático está formado por tres cargas eléctricas puntuales. Dos de ellas tienen idéntico valor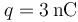 $q=3\,\mathrm{nC}$ y se hallan en los puntos

P 1

y

P 2

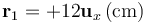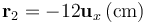, dados por los vectores de posición $\mathbf{r}_1=+12\mathbf{u}_x\,\mathrm{(cm)}$ y $\mathbf{r}_2=-12\mathbf{u}_x\,\mathrm{(cm)}$ , respectivamente. La tercera carga tiene un valor

Q

y se halla en el punto

P 3

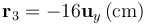, dado por $\mathbf{r}_3=-16\mathbf{u}_y\,\mathrm{(cm)}$ .

Determine, si es posible, el valor que debe tener la carga $Q$ y la posición 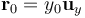$\mathbf{r}_0=y_0\mathbf{u}_y$ de un punto del eje $O Y$ en el cuál se anulen simultáneamente el potencial y el campo eléctrico creado por el sistema de tres cargas.
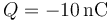¿Cuál es la energía electrostática del sistema descrito en el caso particular $Q=-10\,\mathrm{nC}$ ?
En la situación particular del apartado anterior, ¿qué trabajo hay que realizar para traer una carga $q$ desde el infinito hasta el punto de posición 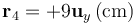$\mathbf{r}_4=+9\mathbf{u}_y\,\mathrm{(cm)}$ . ¿Cuánto vale la fuerza electrostática ejercida sobre dicha carga este punto?
Determine los momentos monopolar y dipolar de la distribución correspondiente al apartado 2. Halle el potencial exacto y el aproximado por el desarrollo multipolar, para el punto 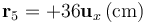$\mathbf{r}_5=+36\mathbf{u}_x\,\mathrm{(cm)}$ . Calcule el error relativo cometido en la aproximación, según la fórmula

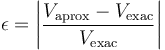
$\epsilon=\left|\frac{V_\mathrm{aprox}-V_\mathrm{exac}}{V_\mathrm{exac}}\right|$

2 Solución

2.1 Punto de campo eléctrico y potencial nulos

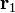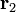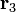Sean tres cargas puntuales $q 1$ , $q 2$ y $q 3$ , situadas en los puntos $P 1$ , $P 2$ y $P 3$ , cuyas posiciones respecto de un punto fijo $O$ (origen de un sistema de referencia), están determiandas por sendos vectores $\mathbf{r}_1$ , $\mathbf{r}_2$ y $\mathbf{r}_3$ . El campo eléctrico y el potencial electrostático creado por el sistema en un punto $P$ , descrito por el radiovector $\mathbf{r}$ , responden a las siguientes expresiones:

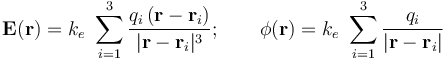
$\mathbf{E}(\mathbf{r})=k_e \ \sum_{i=1}^3\frac{q_i\!\ (\mathbf{r}-\mathbf{r}_i)}{|\mathbf{r}-\mathbf{r}_i|^3}\mathrm{;}\,\qquad\phi(\mathbf{r})=k_e \ \sum_{i=1}^3\frac{q_i}{|\mathbf{r}-\mathbf{r}_i|}$

donde el valor de la constante

k e

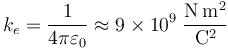en el Sistema Internacional (SI) es, $\displaystyle k_e=\frac{1}{4\pi\varepsilon_0}\approx 9\times 10^9\;\frac{\mathrm{N}\,\mathrm{m}^2}{\mathrm{C}^2}$ .

En el sistema bajo estudio hay dos cargas de valor conocido, alineadas en la dirección que definiremos como eje $O X$ del sistema de referencia cartesiano que utilizaremos para la descripción analítica de las magnitudes vectoriales. La tercera carga, de valor no determinado inicialmente, se encuentra en la recta perpendicular al segmento 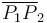$\overline{P_1P}_2$ (cuyos extremos son las otras dos cargas), y que corta a éste en su punto medio $O$ . Tomaremos este punto como origen del sistema de refencia, y a la tercera carga situada en el semieje negativo de $O Y$ . De esta forma se tendrá,

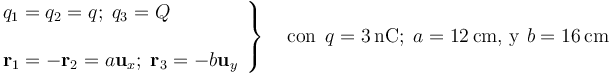
$\left.\begin{array}{l}q_1=q_2=q\mathrm{;}\,\;q_3=Q\\ \\ \mathbf{r}_1=-\mathbf{r}_2=a\mathbf{u}_x\mathrm{;}\,\;\mathbf{r}_3=-b\mathbf{u}_y\end{array}\right\}\quad\mathrm{con}\,\;q=3\,\mathrm{nC;}\;\, a=12\,\mathrm{cm,}\,\,\mathrm{y}\,\, b=16\,\mathrm{cm}$

Para determinar el valor de $Q$ se pide que éste debe ser tal que haya un $P 0$ del eje $O Y$ en que se anulen simultáneamente el campo eléctrico y el potencial creados por el sistema electrostático de tres cargas. La posición de dicho punto vendrá dada por una radiovector 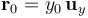$\mathbf{r}_0=y_0\!\ \mathbf{u}_y$ , de componente desconocida. Para calcular los valores de estas incógnitas resolvemos las ecuaciones algebraicas que se obtienen de las siguientes expresiones:

$\left.\begin{array}{l}\displaystyle\mathbf{E}(\mathbf{r}_0)=k_e \!\ \left[\frac{q\!\ (y_0\!\ \mathbf{u}_y-a\!\ \mathbf{u}_x)}{(y_0^2+a^2)^{3/2}}+\frac{q\!\ (y_0\!\ \mathbf{u}_y+a\!\ \mathbf{u}_x)}{(y_0^2+a^2)^{3/2}}+\frac{Q\!\ (y_0+b) \!\ \mathbf{u}_y}{(y_0+b)^3}\right]=\mathbf{0}\\ \\ \displaystyle \phi(\mathbf{r}_0)=k_e \!\ \left[\frac{2\!\ q}{(y_0^2+a^2)^{1/2}}+\frac{Q}{y_0+b}\right]=0\end{array}\right\}\;\Longrightarrow\;\left\{\begin{array}{l}\displaystyle\frac{2\!\ q\!\ y_0}{(y_0^2+a^2)^{3/2}}=-\frac{Q}{(y_0+b)^2}\\ \\ \displaystyle \frac{2\!\ q}{(y_0^2+a^2)^{1/2}}=-\frac{Q}{y_0+b}\end{array}\right.$

Este sistema de ecuaciones se resuelve fácilmente sin mas que dividir la primera ecuación entre la segunda:

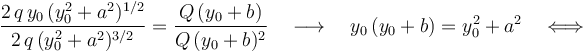
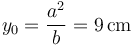
$\frac{2\!\ q\!\ y_0\!\ (y_0^2+a^2)^{1/2}}{2\!\ q\!\ (y_0^2+a^2)^{3/2}}=\frac{Q\!\ (y_0+b)}{Q\!\ (y_0+b)^2}\quad\longrightarrow\quad y_0\!\ (y_0+b)=y_0^2+a^2\quad\Longleftrightarrow$ $y_0=\frac{a^2}{b}=9\,\mathrm{cm}$

... y sustituyendo este resultado en la segunda de las ecuaciones algebraicas anteriores...

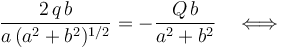
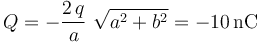
$\frac{2\!\ q\!\ b}{a\!\ (a^2+b^2)^{1/2}}=-\frac{Q\!\ b}{a^2+b^2}\quad\Longleftrightarrow$ $Q=-\frac{2\!\ q}{a}\ \sqrt{a^2+b^2}=-10\,\mathrm{nC}$

2.2 Energía electrostática del sistema

Una vez obtenido el valor de la carga $Q$ que, no por casualidad, coincide con el nuevo dato de 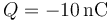$Q=-10\,\mathrm{nC}$ proporcionado en este apartado, continuamos con el análisis del sistema electrostático bajo estudio, calculando su energía electrostática que, por definición, es la suma de los trabajos externos $W i$ que es necesario realizar para traer cada una de las cargas puntuales desde el infinito hasta sus correspondientes posiciones en el sistema. En el caso que nos ocupa,

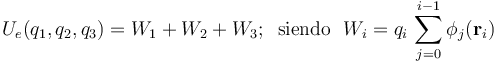
$U_e(q_1\mathrm{,}\,q_2\mathrm{,}\,q_3)=W_1+W_2+W_3\mathrm{;}\,\;\;\mathrm{siendo}\,\;\,W_i=q_i\!\ \sum_{j=0}^{i-1}\phi_j(\mathbf{r}_i)$

Obsérvese que para calcular dichos trabajos externos aplicamos el concepto de potencial electrostático en un punto como el trabajo que es necesario realizar por unidad de carga, para traer una carga puntual desde dicho el infinito hasta dicho punto. De esta forma, el $W i$ para cada carga está determinado por la propia carga y la superposición de los potenciales $\phi_j(\mathbf{r})$ creados por las que se trajeron previamente. 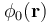Por otra parte, $\phi_0(\mathbf{r})$ sería un posible campo potencial existente en la región, previamente a que se trajesen las cargas y, por tanto, creado por otras distribuciones.

En el sistema bajo estudio, se considera que no hay distribuciones previas, de manera que el proceso para traer la primera carga al sistema se lleva a cabo sin necesidad de realizar trabajo alguno:

$\phi_0(\mathbf{r})=0\mathrm{,}\,\;\,\forall\,P\in\mathrm{I}\! \mathrm{R}^3\quad\Longrightarrow\quad W_1=q_1\!\ \phi_0(\mathbf{r}_1)=0$

El trabajo para traer la segunda carga hasta el punto $P 2$ , enpresencia de la traída anteriormente es:

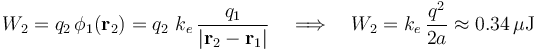
$W_2=q_2\!\ \phi_1(\mathbf{r}_2)=q_2\ k_e\!\ \frac{q_1}{|\mathbf{r}_2-\mathbf{r}_1|}\quad\Longrightarrow\quad W_2=k_e\!\ \frac{q^2}{2a}\approx 0.34\,\mu\mathrm{J}$

Finalmente, el trabajo que ha de realizarse para traer la carga $q 3$ contra el campo creado por $q 1$ y $q 2$ , es:

$W_3=q_3\!\ \big[\phi_1(\mathbf{r}_3)+\phi_2(\mathbf{r}_3)\big]=q_3\!\ k_e\ \left[\frac{q_1}{|\mathbf{r}_3-\mathbf{r}_1|}+\frac{q_2}{|\mathbf{r}_3-\mathbf{r}_2|}\right]\quad\Longrightarrow\quad W_3=k_e\!\ \frac{2\!\ q\!\ Q}{\sqrt{a^2+b^2}}\approx -2.70\,\mu\mathrm{J}$

Por tanto, la energía electrostática del sistema es:

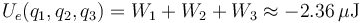
$U_e(q_1\mathrm{,}\,q_2\mathrm{,}\,q_3)=W_1+W_2+W_3\approx -2.36\,\mu\mathrm{J}$

Puede seguirse otro procedimiento para obtener el valor de la energía electrostática del sistema. Al ser ésta una función de estado y, por tanto, su valor no puede depender del orden seguido para reunir las cargas, se puede desmostrar que la energía electrostática del sistema es igual a la mitad de la suma de las energías potenciales de cada una de las cargas al encontrarse sometidas al campo eléctrico creado por las otras dos:

$\begin{array}{c}\displaystyle U_e(q_1\mathrm{,}\,q_2\mathrm{,}\,q_3)=\frac{1}{2}\!\ \big[U_e(q_1;P_1)+U_e(q_2;P_2)+U_e(q_3;P_3)\big]\mathrm{;}\\ \\ \displaystyle\mathrm{con}\,\;\,U_e(q_i;P_i)=q_i\ k_e\!\ \left[\frac{q_j}{|\mathbf{r}_i-\mathbf{r}_j|}+\frac{q_k}{|\mathbf{r}_i-\mathbf{r}_k|}\right]\mathrm{,}\,\;\; i\neq j\neq k\neq i\end{array}$

Puede comprobarse que el resultado que se obtiene es el mismo que con el procedimiento empleado anteriormente.

2.3 Trabajo y fuerza sobre otra carga

Una nueva carga puntual de valor

q

se trae desde el infinito hasta una posición

P 4

en el eje

O Y

, en presencia de las tres cargas consideradas en los apartados anteriores. El trabajo externo que es necesario realizar para llevar a cabo tal operación, y la fuerza que actúa sobre la carga en su posición final, estarán determinados por las siguientes expresiones: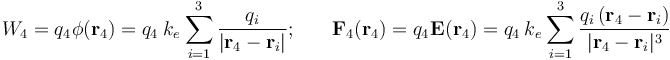 $W_4=q_4\!\ \phi(\mathbf{r}_4)=q_4\ k_e \!\ \sum_{i=1}^3\frac{q_i}{|\mathbf{r}_4-\mathbf{r}_i|}\mathrm{;}\qquad\mathbf{F}_4(\mathbf{r}_4)=q_4\!\ \mathbf{E}(\mathbf{r}_4)=q_4\ k_e \!\ \sum_{i=1}^3\frac{q_i\!\ (\mathbf{r}_4-\mathbf{r}_i)}{|\mathbf{r}_4-\mathbf{r}_i|^3}$

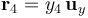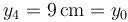Obsérvese que la posición del punto $P 4$ viene dada por el radiovector $\mathbf{r}_4=y_4\!\ \mathbf{u}_y$ , con $y_4=9\,\mathrm{cm}=y_0$ . En consecuencia, dicho punto coincide con el $P 0$ que se determinó en el primer apartado, donde se anularían el potencial y el campo eléctrico creado por las tres primeras cargas si 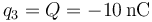$q_3=Q=-10\,\mathrm{nC}$ . En el enunciado se indica explícitamente que se verifican dichas condiciones. Por tanto,

$\mathbf{r}_4=\mathbf{r}_0\quad\Longrightarrow\quad\left\{\begin{array}{l}\displaystyle\phi(\mathbf{r}_4)=\phi(\mathbf{r}_0)= k_e \!\ \left(\frac{2q}{\sqrt{a^2+y_0^2}}+\frac{Q}{b+y_0}\right)=0\\ \\ \displaystyle\mathbf{E}(\mathbf{r}_4)=\mathbf{E}(\mathbf{r}_0)=k_e \!\ \left[\frac{2\!\ q\!\ y_0}{(y_0^2+a^2)^{3/2}}+\frac{Q}{(y_0+b)^2}\right]\!\ \mathbf{u}_y=\mathbf{0}\end{array}\right\}\;\Longrightarrow$ $W_4=0\mathrm{;}\,\quad\mathbf{F}_4(\mathbf{r}_4)=\mathbf{0}$

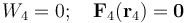
2.4 Desarrollo multipolar

Para cada distribución estática de carga eléctrica existe un sistema equivalente, en el sentido de que crean idéntico campo y potencial eléctrico. Dicho sistema está formado por una secuencia de entes puntales (ideales) situados en un mismo punto arbitrario (centro de reducción), y que contribuyen al potencial con funciones de la posición de alcance decreciente.

2.4.1 Momentos monopolar y dipolar del sistema

Son los dos primeros elementos de dicha secuencia. Si tomamos el origen $O$ del sistema de referencia como centro de reducción, estos entes son equivalentes a una carga $Q 0$ y a un dipolo puntual 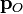$\mathbf{p}_O$ colocados en aquél punto. Aplicando su definición en el sistema bajo estudio tendremos:

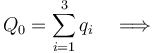
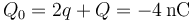
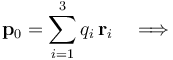
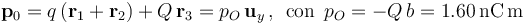
$Q_0=\sum_{i=1}^3q_i\quad\Longrightarrow$ $Q_0=2q+Q=-4\, \mathrm{nC}$ $\mathbf{p}_0=\sum_{i=1}^3q_i\!\ \mathbf{r}_i\quad\Longrightarrow$ $\mathbf{p}_0=q\!\ (\mathbf{r}_1+\mathbf{r}_2)+Q\!\ \mathbf{r}_3=p_O\!\ \mathbf{u}_y\,\mathrm{,}\,\;\,\mathrm{con}\,\; p_O=-Q\!\ b=1.60\,\mathrm{nC}\!\ \mathrm{m}\,$

2.4.2 Potencial exacto y aproximado en un punto

Consideramos el punto $P 5$ situado en el eje $O X$ , cuya posición respecto del origen $O$ viene dada por el radiovector 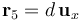$\mathbf{r}_5=d\!\ \mathbf{u}_x$ , siendo 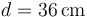$d=36\,\mathrm{cm}$ . El valor exacto del potencial en dicho punto es:

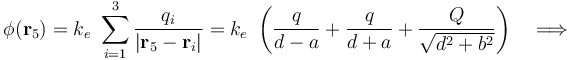
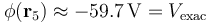
$\phi(\mathbf{r}_5)=k_e\ \sum_{i=1}^3\frac{q_i}{|\mathbf{r}_5-\mathbf{r}_i|}=k_e\ \left(\frac{q}{d-a}+\frac{q}{d+a}+\frac{Q}{\sqrt{d^2+b^2}}\right)\quad\Longrightarrow$ $\phi(\mathbf{r}_5)\approx-59.7\,\mathrm{V}=V_\mathrm{exac}$

Pero también podemos obtener un valor aproximado del potencial utilizando las contribuciones de los dos momentos calculados:

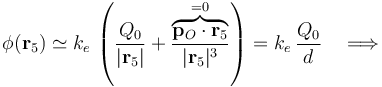
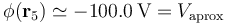
$\phi(\mathbf{r}_5)\simeq k_e\!\ \left( \frac{Q_0}{|\mathbf{r}_5|}+\frac{\overbrace{\mathbf{p}_O\cdot\mathbf{r}_5}^{=0}}{|\mathbf{r}_5|^3}\right)=k_e\!\ \frac{Q_0}{d}\quad\Longrightarrow$ $\phi(\mathbf{r}_5)\simeq-100.0\,\mathrm{V}=V_\mathrm{aprox}$

En consecuencia, el error relativo que se comete si se utiliza la aproximación en lugar del valor exacto es:

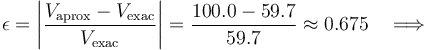
$\epsilon=\left|\frac{V_\mathrm{aprox}-V_\mathrm{exac}}{V_\mathrm{exac}}\right|=\frac{100.0-59.7}{59.7}\approx 0.675\quad\Longrightarrow$

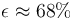
$\Longrightarrow$ $\epsilon\approx68\%$

Este resultado nos indica que la contribución de los dos primeros términos del desarrollo multipolar (incluso a distancias mayores que el tamaño del sistema) no proporciona una buena aproximación para el valor del potencial, al menos en los puntos $P$ del plano $O X Z$ . Esto se debe a que, para estos puntos, el vector posición 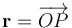$\mathbf{r}=\overrightarrow{OP}$ es perpendicular al momento dipolar 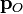$\mathbf{p}_O$ y, por tanto, éste no contribuye al valor aproximado del potencial. Para obtener una mejor aproximación con el desarrollo multipolar habrían de incluirse alguno de los términos siguientes; al menos, la contribución de un cuadrupolo (momento cuadrupolar de la distribución) colocado en el punto $O$ .

Sistema electrostático de tres cargas puntuales

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Punto de campo eléctrico y potencial nulos

2.2 Energía electrostática del sistema

2.3 Trabajo y fuerza sobre otra carga

2.4 Desarrollo multipolar

2.4.1 Momentos monopolar y dipolar del sistema

2.4.2 Potencial exacto y aproximado en un punto

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES