Entrar Página Discusión Historial Go to the site toolbox

Campo eléctrico entre dos varillas

De Laplace

Contenido

1 Enunciado

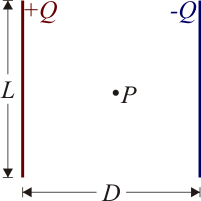
Dos varillas rectilíneas de longitud L están situadas paralelamente a una distancia D. Las varillas poseen cargas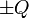 \pm Q distribuidas uniformemente.
  1. Halle aproximadamente el campo eléctrico en un punto P equidistante de ambas varillas, para el caso D\gg L.
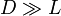  2. Calcule, también de forma aproximada, el valor del campo en el mismo punto P, para el caso D\ll L.
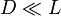  3. Calcule el valor exacto del campo eléctrico en dicho punto P, para un valor arbitrario de D.
  4. Compare los valores exactos y aproximados para el caso 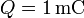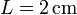Q=1\,\mathrm{mC}, L=2\,\mathrm{cm}, y
    1. D=2\,\mathrm{mm}
    2. D=40\,\mathrm{cm}

2 Caso de dos varillas muy alejadas

Si la distancia entre las varillas es muy grande, comparada con su tamaño, desde el punto central se apreciará cada una aproximadamente como una carga puntual.

La distancia de P a esas cargas puntuales será, también aproximadamente, D / 2. Los campos debidos a cada carga serán iguales en el punto central y ambos irán de la varilla positiva a la negativa (dirección y sentido de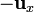 -\mathbf{u}_{x}. Por tanto, el campo en P vale aproximadamente
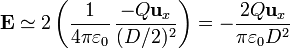
\mathbf{E} \simeq 2\left(\displaystyle\frac{1}{4\pi\varepsilon_0}\,\frac{-Q\mathbf{u}_{x}}{(D/2)^2}\right) = -\frac{2Q\mathbf{u}_{x}}{\pi\varepsilon_0 D^2}

Este campo tiende a cero cuando 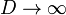D\to\infty, pero no se trata de hallar su valor límite (nulo), sino de estudiar cómo se comporta para distancias grandes.

3 Caso de dos varillas muy próximas

Cuando la distancia entre las varillas es muy corta comparada con su longitud, podemos aproximar cada varilla como una línea infinita de carga, con densidad de carga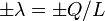 \pm\lambda = \pm Q/L.

El campo creado por una línea infinita de carga situada en el eje z puede calcularse bien por integración directa, bien por aplicación de la ley de Gauss (como en otro problema). En cualquier caso, el campo que produce, en cartesianas, es

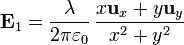
\mathbf{E}_1 = \frac{\lambda}{2\pi\varepsilon_0}\,\frac{x\mathbf{u}_{x}+y\mathbf{u}_{y}}{x^2+y^2}

Si la varilla no está en el eje z sino en x' = D / 2, y' = 0 el campo es

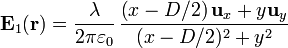
\mathbf{E}_1(\mathbf{r}) = \frac{\lambda}{2\pi\varepsilon_0}\,\frac{\left(x-D/2\right)\mathbf{u}_{x}+y\mathbf{u}_{y}}{(x-D/2)^2+y^2}


El campo debido a esta varilla, en el punto P (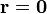\mathbf{r}=\mathbf{0}) será, sustituyendo

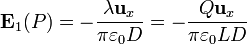
\mathbf{E}_1(P)= -\frac{\lambda \mathbf{u}_{x}}{\pi\varepsilon_0 D} = -\frac{Q\mathbf{u}_{x}}{\pi\varepsilon_0 L D}

Éste es el campo debido a la varilla cargada positivamente. El de la cargada negativamente se obtiene del mismo modo, considerando carga opuesta y posición en x' = − D / 2. El resultado es exactamente el mismo, por lo que el campo total es el doble del que crea una sola de las varillas

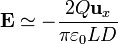
\mathbf{E}\simeq -\frac{2Q\mathbf{u}_{x}}{\pi\varepsilon_0 L D}

Este campo tiende a infinito para 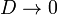D\to 0, pero de nuevo se trata de estudiar su comportamiento, no de hallar su valor límite.

4 Caso general

El cálculo exacto debe hacerse por integración directa, ya que la ley de Gauss no es útil en el caso de una varilla de longitud finita.

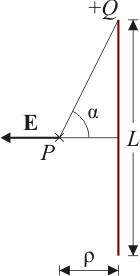
Para hacer el calculo exacto debemos hallar el campo eléctrico en el plano medio de un hilo cargado uniformemente de longitud L. Podemos calcularlo como caso particular del campo creado por un segmento en un punto arbitrario del espacio. No obstante, dada la simetría del plano central, es más sencillo calcularlo directamente. En este caso tomamos el eje Z coincidente con el hilo y el origen de coordenadas en su centro. El campo en un punto de vector \mathbf{r} es

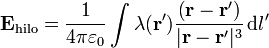
\mathbf{E}_{\mathrm{hilo}} = \frac{1}{4\pi\varepsilon_0}\int\lambda(\mathbf{r}')\frac{\left(\mathbf{r}-\mathbf{r}'\right)}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}l'

Usando coordenadas cilíndricas se tiene

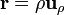
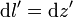
\mathbf{r} = \rho\mathbf{u}_{\rho}    \mathbf{r}' = z'\mathbf{u}_{z}\quad z\in[-L/2,L/2]    \mathrm{d}l' = \mathrm{d}z'\,

El campo es

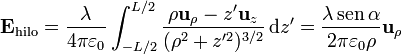
\mathbf{E}_{\mathrm{hilo}} = \frac{\lambda}{4\pi\varepsilon_0} \int_{-L/2}^{L/2} \frac{\rho\mathbf{u}_{\rho}-z'\mathbf{u}_{z}} {(\rho^2+z'^2)^{3/2}}\,\mathrm{d}z' = \frac{\lambda\,\mathrm{sen}\,{\alpha}}{2\pi\varepsilon_0\rho}\mathbf{u}_{\rho}

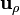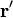siendo α el ángulo indicado en la figura. Obsérvese que en esta integral no hace falta pasar \mathbf{u}_{\rho} a la base cartesiana porque al provenir de \mathbf{r} (y no de \mathbf{r}') funciona como una constante en la integral.

El campo es radial en el plano medio, pues la suma de las componentes en el eje Z se anula. Observando la figura se ve que
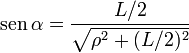
\mathrm{sen}\,{\alpha} = \frac{L/2}{\sqrt{\rho^2+(L/2)^2}}

Por tanto

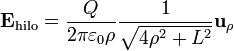
\mathbf{E}_{\mathrm{hilo}} =\frac{Q}{2\pi\varepsilon_0\rho}\frac{1}{\sqrt{4\rho^2+L^2}}\mathbf{u}_{\rho}
Ahora hemos de aplicar este resultado a nuestro problema. Si consideramos el hilo positivo, el campo apunta a lo largo del eje X y en sentido negativo. La distancia del punto medio entre los hilos al centro del hilo es ρ = D / 2. Entonces el campo del hilo positivo es
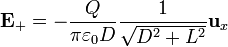
\mathbf{E}_+ = -\frac{Q}{\pi\varepsilon_0D}\frac{1}{\sqrt{D^2+L^2}}\mathbf{u}_x

Para el hilo negativo el campo en ese punto es el mismo, como en los apartados anteriores. El campo total es la suma de los dos

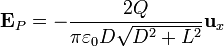
\mathbf{E}_P = -\frac{2Q}{\pi\varepsilon_0D\sqrt{D^2+L^2}}\mathbf{u}_{x}

5 Comparación con los casos aproximados

5.1 Caso de segmentos muy alejados

Cuando 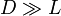D\gg L podemos despreciar L frente a D en la expresión exacta, de forma que tenemos

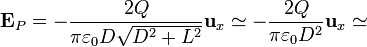
\mathbf{E}_P = -\frac{2Q}{\pi\varepsilon_0D\sqrt{D^2+L^2}}\mathbf{u}_{x}\simeq -\frac{2Q}{\pi\varepsilon_0D^2}\mathbf{u}_{x}\simeq

que es la expresión que obtuvimos a partir de la aproximación de las varillas mediante cargas puntuales.

Podemos hacer una estimación del error cometido. Una posibilidad es acudir a la definición de error relativo

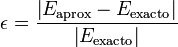
\epsilon = \frac{\left|E_\mathrm{aprox}-E_\mathrm{exacto}\right|}{\left|E_\mathrm{exacto}\right|}

que, sustituyendo y eliminando los factores comunes nos da

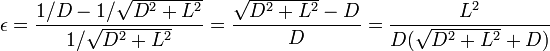
\epsilon = \frac{1/D-1/\sqrt{D^2+L^2}}{1/\sqrt{D^2+L^2}} = \frac{\sqrt{D^2+L^2}-D}{D} = \frac{L^2}{D(\sqrt{D^2+L^2}+D)}

(en el último paso, para evitar indeterminaciones se multiplica por el conjugado del numerador).

Cuando 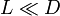L \ll D este error vale aproximadamente

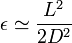
\epsilon\simeq \frac{L^2}{2D^2}

esto quiere decir que si, por ejemplo L = 2cm y 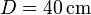D=40\,\mathrm{cm}, el error cometido es aproximadamente

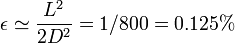
\epsilon\simeq \frac{L^2}{2D^2} = 1/800 = 0.125\%

una décima de un 1%. Vemos que la aproximación por cargas puntuales da un error muy pequeño y es perfectamente válida.

Otra forma de calcular el error es a partir de la serie de Taylor de la raíz. Se tiene que`, por la ´formula del binomio de Newton

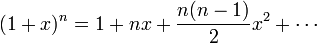
(1 + x)^n = 1 + nx + \frac{n(n-1)}{2}x^2 + \cdots    x\ll 1

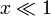
lo que en nuestro caso da

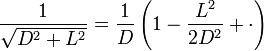
\frac{1}{\sqrt{D^2+L^2}} = \frac{1}{D}\left(1-\frac{L^2}{2D^2}+\cdot\right)

con lo que el error relativo es el factor que corrige al 1 en el paréntesis anterior, resultando la expresión que ya conocemos.

5.2 Caso de segmentos muy próximos

En el caso contrario, 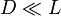D\ll L lo que se puede despreciar es D en su suma frente a L en la expresión exacta, de forma que tenemos

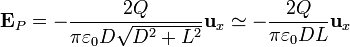
\mathbf{E}_P = -\frac{2Q}{\pi\varepsilon_0D\sqrt{D^2+L^2}}\mathbf{u}_{x}\simeq -\frac{2Q}{\pi\varepsilon_0DL}\mathbf{u}_{x}

que es la expresión que obtuvimos a partir de la aproximación de las varillas por hilos infinitos.

La estimación del error relativo cometido es ahora

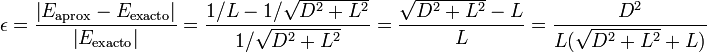
\epsilon = \frac{\left|E_\mathrm{aprox}-E_\mathrm{exacto}\right|}{\left|E_\mathrm{exacto}\right|}= \frac{1/L-1/\sqrt{D^2+L^2}}{1/\sqrt{D^2+L^2}} = \frac{\sqrt{D^2+L^2}-L}{L} = \frac{D^2}{L(\sqrt{D^2+L^2}+L)}

y para 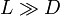L \gg D este error vale

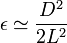
\epsilon\simeq \frac{D^2}{2L^2}

que para el caso L = 2cm y 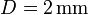D=2\,\mathrm{mm} nos da un error relativo

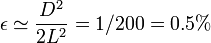
\epsilon\simeq \frac{D^2}{2L^2} = 1/200 = 0.5\%

medio 1%.

Obviamente ambos límites dejan de valer cuando una de las distancias deja de ser mucho más pequeña que la otra. Podemos representar gráficamente estas dos aproximaciones. Puesto que estamos trabajando con funciones que tienden a 0 o a infinito, es conveniente hacer una gráfica log-log. En la figura se ve el campo eléctrico (escalado adecuadamente) como función del del cociente D / L para valores de esta cociente entre una centésima y 100. Cuando la distancia relativa se multiplica por 100, nos movemos dos décadas hacia la derecha. En este gráfica, los caso en que la distancia es mucho menor que la longitud de las varillas quedan a la izquierda, mientra que si es mucho mayor nos situamos a la derecha.

Resulta entonces que, como hemos dicho, para distancias cortas la mejor aproximación es la de dos líneas de carga (cuya gráfica es una línea recta de pendiente -1 en la gráfica log-log). Para grandes distancias, en cambio la mejor aproximación es la de dos cargas puntuales (a la cual corresponde una gráfica de pendiente -2). Ambas aproximaciones fallan cuando 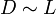D\sim L\, (en el centro de la gráfica). Para esos valores habría que usar la expresión exacta.

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_el%C3%A9ctrico_entre_dos_varillas"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 16:18, 26 oct 2010. - Esta página ha sido visitada 24.564 veces. - Aviso legal - Acerca de Laplace