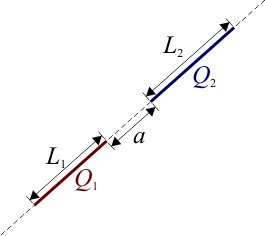
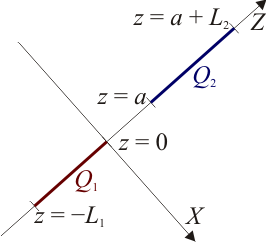Fuerza entre dos varillas colineales

De Laplace

Contenido

1 Enunciado
2 Introducción
3 Campo de la primera varilla
4 Fuerza sobre la segunda varilla
5 El límite de varillas puntuales
6 Fuerza sobre la primera varilla

1 Enunciado

Calcule la fuerza entre dos varillas colineales, de longitudes

L 1

y

L 2

, que almacenan respectivamente cargas

Q 1

y

Q 2

, cuando sus extremos más próximos distan una cantidad

a

.

2 Introducción

la fuerza sobre una distribución de carga que almacena una carga total $Q$ , no es igual al producto de la carga por el campo

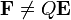
$\mathbf{F}\neq Q\mathbf{E}$

ya que esta expresión solo vale para cargas puntuales. En particular, ¿qué es $\mathbf{E}$ ? ¿El campo en un extremo de la varilla, en el otro, en su punto medio?

La expresión correcta para la fuerza neta sobre un sistema es, como ocurre generalmente en mecánica, la resultante de las fuerzas aplicadas, esto es, la suma vectorial de las fuerzas aplicadas sobre cada punto de la distribución.

Dividiendo una distribución en elementos de volumen, cada uno de los cuales se puede suponer puntual, queda

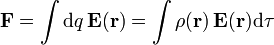
$\mathbf{F}= \int \mathrm{d}q\,\mathbf{E}(\mathbf{r})=\int \rho(\mathbf{r})\,\mathbf{E}(\mathbf{r})\mathrm{d}\tau$

o la expresión correspondiente para una distribución de carga lineal

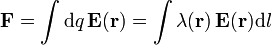
$\mathbf{F}= \int \mathrm{d}q\,\mathbf{E}(\mathbf{r})=\int \lambda(\mathbf{r})\,\mathbf{E}(\mathbf{r})\mathrm{d}l$

En nuestro caso debemos hallar la fuerza entre dos varillas. Empleando el campo eléctrico como intermediario, podemos suponer que una de ellas (la varilla ”1“) crea el campo y la otra (la varilla ”2“) lo experimenta. Sea el segmento 1 el de carga

Q 1

. Este segmento posee longitud

L 1

.

Por comodidad podemos suponer como eje $Z$ el común a ambas varillas, y situar el origen de coordenadas en el extremo de la varilla 1 más próximo a la varilla 2. Supondremos además que la segunda varilla se encuentra en el semieje $z > 0$ , esto es que $z 2 > z 1$ para todos los puntos de las dos varillas.

3 Campo de la primera varilla

Necesitamos calcular el campo eléctrico producido por este segmento, que para una distribución lineal es

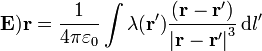
$\mathbf{E})\mathbf{r}=\frac{1}{4\pi\varepsilon_0}\int \lambda(\mathbf{r}')\frac{\left(\mathbf{r}-\mathbf{r}'\right)}{\left|\mathbf{r}-\mathbf{r}'\right|^3}\,\mathrm{d}l'$

No necesitamos conocer el campo en todo el espacio, nos basta con hallarlo en los puntos del propio eje $Z$ situados en $z > 0$ , que es donde se encuentra la segunda varilla. Por tanto, podemos hacer

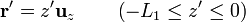
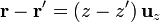$\mathbf{r}= z\mathbf{u}_z$ $\mathbf{r}'= z'\mathbf{u}_z\qquad \left(-L_1\leq z' \leq 0\right)$ $\mathbf{r}-\mathbf{r}'= \left(z- z'\right)\mathbf{u}_z$

d l' = d z'

En cuanto a la densidad de carga, si esta es uniforme, es simplemente

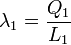
$\lambda_1 = \frac{Q_1}{L_1}$

Todo esto nos deja la expresión del campo como

$\mathbf{E}_1(z) =\frac{1}{4\pi\varepsilon_0}\int_{-L_1}^{0} \frac{Q_1}{L_1}\,\frac{\mathbf{u}_z}{(z-z')^2}\,\mathrm{d}z'$

Esta integral es inmediata:

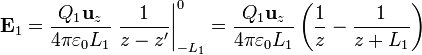
$\mathbf{E}_1 = \frac{Q_1\mathbf{u}_z}{4\pi\varepsilon_0 L_1}\left.\frac{1}{z-z'}\right|_{-L_1}^{0} = \frac{Q_1\mathbf{u}_z}{4\pi\varepsilon_0 L_1}\left(\frac{1}{z}-\frac{1}{z+L_1}\right)$

4 Fuerza sobre la segunda varilla

Una vez que tenemos el campo, podemos calcular la fuerza sobre la segunda varilla. Esta tiene también densidad uniforme

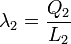
$\lambda_2 = \frac{Q_2}{L_2}$

y ocupa las posiciones

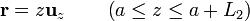$\mathbf{r}= z\mathbf{u}_z\qquad \left(a\leq z \leq a+L_2\right)$

d l = d z

de forma que la fuerza sobre ella es

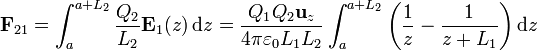
$\mathbf{F}_{21} = \int_{a}^{a+L_2} \frac{Q_2}{L_2}\mathbf{E}_1(z)\,\mathrm{d}z = \frac{Q_1Q_2\mathbf{u}_z}{4\pi\varepsilon_0 L_1L_2}\int_a^{a+L_2}\left(\frac{1}{z}-\frac{1}{z+L_1}\right)\mathrm{d}z$

De nuevo tenemos dos integrales inmediatas, que resultan en sendos logaritmos. Combinado los logaritmos queda finalmente

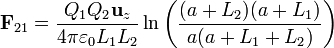
$\mathbf{F}_{21} = \frac{Q_1Q_2\mathbf{u}_z}{4\pi\varepsilon_0 L_1L_2}\ln\left(\frac{(a+L_2)(a+L_1)}{a(a+L_1+L_2)}\right)$

Nótese cómo no resulta 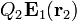$Q_2\mathbf{E}_1(\mathbf{r}_2)$ ya que el campo 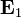$\mathbf{E}_1$ no contiene logaritmos por ningún lado. La fuerza sobre una distribución de carga no coincide con la fuerza sobre una carga puntual.

5 El límite de varillas puntuales

La expresión general de la fuerza depende de las cargas, los tamaños y la distancia entre las varillas. Este resultado, para el caso de que la distancia entre varillas sea mucho mayor que sus tamaños respectivos, debe coincidir con la ley de Coulomb, para la fuerza entre cargas puntuales. Podemos hallar el límite del resultado anterior y comprobar si tiende al valor correcto. Esto nos sirve como test de una condición necesaria (pero no suficiente) para que el resultado anterior sea correcto.

Desarrollando el numerador y el denominador del logaritmo y dividiendo en ambos por $a 2$ nos queda

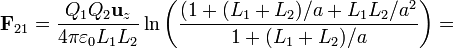
$\mathbf{F}_{21} = \frac{Q_1Q_2\mathbf{u}_z}{4\pi\varepsilon_0 L_1L_2}\ln\left(\frac{(1+(L_1+L_2)/a+L_1L_2/a^2}{1+(L_1+L_2)/a}\right)=$

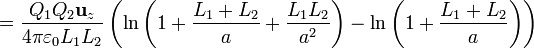
$=\frac{Q_1Q_2\mathbf{u}_z}{4\pi\varepsilon_0 L_1L_2}\left(\ln\left(1+\frac{L_1+L_2}{a}+\frac{L_1L_2}{a^2}\right)- \ln\left(1+\frac{L_1+L_2}{a}\right)\right)$

Ahora bien, por ser 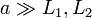$a\gg L_1,L_2$ podemos aplicar la serie de Taylor del logaritmo

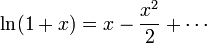
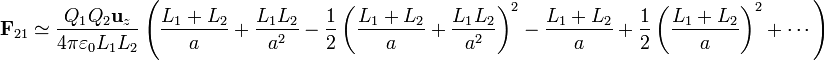
$\ln(1+x) = x-\frac{x^2}{2}+\cdots$ y resulta $\mathbf{F}_{21}\simeq\frac{Q_1Q_2\mathbf{u}_z}{4\pi\varepsilon_0 L_1L_2}\left(\frac{L_1+L_2}{a}+\frac{L_1L_2}{a^2}-\frac{1}{2}\left(\frac{L_1+L_2}{a}+\frac{L_1L_2}{a^2}\right)^2-\frac{L_1+L_2}{a}+\frac{1}{2}\left(\frac{L_1+L_2}{a}\right)^2+\cdots\right)$

Si nos quedamos con los primeros términos que no se anulan mutuamente nos queda

$\mathbf{F}_{21}\simeq\frac{Q_1Q_2\mathbf{u}_z}{4\pi\varepsilon_0 L_1L_2}\left(\frac{L_1L_2}{a^2}\right)= \frac{Q_1Q_2\mathbf{u}_z}{4\pi\varepsilon_0 a^2}$

que es la expresión de la ley de Coulomb para dos cargas puntuales $Q 1$ y $Q 2$ separadas una distancia $a$ .

6 Fuerza sobre la primera varilla

La fuerza sobre la varilla 1 la podemos obtener por simple aplicación de la tercera ley de Newton

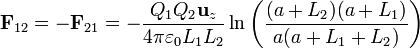
$\mathbf{F}_{12}=-\mathbf{F}_{21} =-\frac{Q_1Q_2\mathbf{u}_z}{4\pi\varepsilon_0 L_1L_2}\ln\left(\frac{(a+L_2)(a+L_1)}{a(a+L_1+L_2)}\right)$

obsérvese que este resultado no es exactamente el mismo que resulta si cambiamos $Q 1$ por $Q 2$ y $L 1$ por $L 2$ en la expresión de 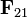$\mathbf{F}_{21}$ (si hiciéramos esto saldría con signo positivo). La razón está en que al orientar los ejes supusimos que el sentido positivo del eje $Z$ era el que iba de la varilla 1 a la 2. 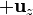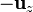Si lo que queremos es hallar la fuerza de la 2 sobre la 1 debemos cambiar $Q 1$ por $Q 2$ , $L 1$ por $L 2$ y además $+\mathbf{u}_z$ por $-\mathbf{u}_z$ . Entonces sí se obtiene el resultado anterior, en completo acuerdo con la tercera ley de Newton.