Campo eléctrico con simetría cilíndrica

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Un campo eléctrico con simetría cilíndrica está definido por la siguiente expresión, expresada en coordenadas cilíndricas:

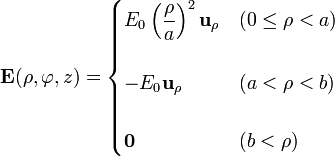
$\mathbf{E}(\rho,\varphi,z)=\begin{cases} \displaystyle E_0\left(\frac{\rho}{a}\right)^2\mathbf{u}_\rho & (0\leq\rho<a)\\ & \\ \displaystyle -E_0\mathbf{u}_\rho\, & (a<\rho< b) \\ & \\ \mathbf{0} & (b<\rho)\end{cases}$

Determine las distribuciones de carga que producen este campo eléctrico, así como la carga eléctrica total.
Obtenga la expresión del potencial electrostático creado por esas distribuciones.
Halle la energía electrostática almacenada entre dos planos $z = 0$ y $z = h$ .

2 Solución

2.1 Distribuciones de carga

En este sistema podemos tener distribuciones de carga de volumen y de superficie.

2.1.1 Distribución volumétrica

La densidad de carga de volumen, $ρ$ , la podemos calcular aplicando la ley de Gauss en forma diferencial

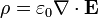
$\rho = \varepsilon_0\nabla\cdot\mathbf{E}$

Tenemos tres regiones, en cada una de las cuales la densidad tiene una expresión diferente

Para $0 < ρ < a$ , calculamos la divergencia empleando coordenadas cilíndricas

$\rho = \varepsilon_0\mathbf{E}= \frac{\varepsilon_0}{\rho}\frac{\mathrm{d}\ }{\mathrm{d}\rho}\left(\rho E_0\frac{\rho^2}{a^2}\right) = \frac{3\varepsilon_0E_0\rho}{a^2}$

Para $a < ρ < b$ , empleando el mismo procedimiento

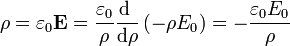
$\rho = \varepsilon_0\mathbf{E}= \frac{\varepsilon_0}{\rho}\frac{\mathrm{d}\ }{\mathrm{d}\rho}\left(-\rho E_0\right) = -\frac{\varepsilon_0E_0}{\rho}$

Para $b < ρ$ el campo es nulo, y su divergencia, también

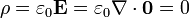
$\rho = \varepsilon_0\mathbf{E}= \varepsilon_0\nabla\cdot\mathbf{0}=0$

2.1.2 Distribución superficial

Además de las cargas en el volumen, podemos tener densidades superficiales de carga en las superficies en que el campo sea discontinuo. Esta densidad la da el salto en las componentes normales del campo eléctrico

$\sigma_s = \varepsilon_0\mathbf{n}\cdot[\mathbf{E}]$

Tenemos dos posibilidades

En $ρ = a$ , el vector normal es 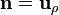$\mathbf{n}=\mathbf{u}_\rho$ , y la densidad de carga

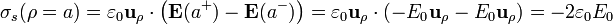
$\sigma_s(\rho=a) = \varepsilon_0\mathbf{u}_\rho\cdot\left(\mathbf{E}(a^+)-\mathbf{E}(a^-)\right) = \varepsilon_0\mathbf{u}_\rho\cdot\left(-E_0\mathbf{u}_\rho-E_0\mathbf{u}_\rho\right)=-2\varepsilon_0E_0$

En $ρ = b$ , operando del mismo modo,

$\sigma_s(\rho=b) = \varepsilon_0\mathbf{u}_\rho\cdot\left(\mathbf{E}(b^+)-\mathbf{E}(b^-)\right) = \varepsilon_0\mathbf{u}_\rho\cdot\left(0\mathbf{u}_\rho-(-E_0)\mathbf{u}_\rho\right)=\varepsilon_0E_0$

Reuniendo todos los resultados, tenemos las densidades de carga

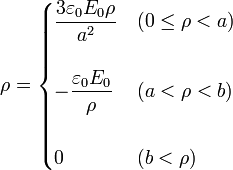
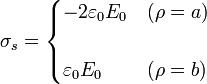
$\rho=\begin{cases} \displaystyle \frac{3\varepsilon_0E_0\rho}{a^2} & (0\leq\rho<a)\\ & \\ \displaystyle -\frac{\varepsilon_0E_0}{\rho} & (a<\rho< b) \\ & \\ 0 & (b<\rho)\end{cases}$ $\sigma_s=\begin{cases} \displaystyle -2\varepsilon_0E_0 & (\rho=a)\\ & \\ \displaystyle \varepsilon_0E_0 & (\rho= b) \end{cases}$

2.1.3 Carga total

La carga total de la distribución es nula, ya que lo es el campo exterior a la distribución. Por aplicación de la ley de Gauss a una superficie exterior al cilindro

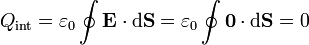
$Q_\mathrm{int}=\varepsilon_0\oint\mathbf{E}\cdot\mathrm{d}\mathbf{S}=\varepsilon_0\oint\mathbf{0}\cdot\mathrm{d}\mathbf{S}=0$

Podemos obtener también este resultado integrando las densidades de carga calculadas en el apartado anterior (lo que, en esencia, consiste en reobtener el campo que derivamos para hallarlas).

Puesto que la longitud de la distribución es infinita, la cantidad de carga almacenada en cada región también lo es. Lo que se anula es la carga neta. Para evitar singularidades, hallaremos la carga por unidad de longitud, considerando la porción de cilindro contenida entre dos planos paralelos $z = 0$ y $z = h$ .

Calculando cada una de las contribuciones

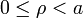
En $0\leq\rho< a$

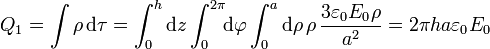
$Q_1 = \int\rho\,\mathrm{d}\tau=\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\int_0^a \mathrm{d}\rho\,\rho\,\frac{3\varepsilon_0E_0\rho}{a^2}=2\pi ha\varepsilon_0E_0$

En $ρ = a$

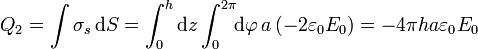
$Q_2 = \int\sigma_s\,\mathrm{d}S=\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\,a\,(-2\varepsilon_0E_0)=-4\pi ha\varepsilon_0E_0$

En $a < ρ < b$

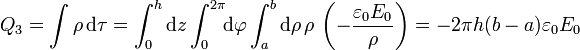
$Q_3 = \int\rho\,\mathrm{d}\tau=\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\int_a^b \mathrm{d}\rho\,\rho\,\left(-\frac{\varepsilon_0E_0}{\rho}\right)=-2\pi h(b-a)\varepsilon_0E_0$

En $ρ = b$

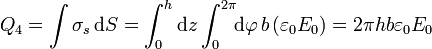
$Q_4 = \int\sigma_s\,\mathrm{d}S=\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\,b\,(\varepsilon_0E_0)=2\pi hb\varepsilon_0E_0$

En $b < ρ$

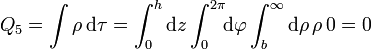
$Q_5 = \int\rho\,\mathrm{d}\tau=\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\int_b^\infty \mathrm{d}\rho\,\rho\,0=0$

Sumando las cinco contribuciones

$Q=Q_1+Q_2+Q_3+Q_4+Q_5 = 2\pi h\varepsilon_0E_0\left(a-2a-(b-a)+b+0\right)=0$

en completo acuerdo con el resultado anterior. De hecho, este segundo método sirve como test para ver que las densidades de carga no fueran calculadas incorrectamente.

2.2 Potencial eléctrico

Este segundo apartado es completamente independiente del anterior, ya que no se trata de hallar el potencial eléctrico por integración directa a partir de las densidades de carga obtenidas (lo que sería una tarea hercúlea), sino a partir del campo eléctrico, mediante la integral de camino

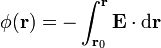
$\phi(\mathbf{r}) = -\int_{\mathbf{r}_0}^\mathbf{r}\mathbf{E}\cdot\mathrm{d}\mathbf{r}$

Tomamos como origen de potencial el infinito y como camino de integración uno radial horizontal, de forma que

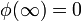
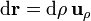
$\phi(\infty)=0\,$ $\mathrm{d}\mathbf{r}=\mathrm{d}\rho\,\mathbf{u}_\rho$

Al hacer la integral debemos distinguir tres regiones,

Para $ρ > b$ , debemos integrar un campo que es nulo en todos los puntos del camino de integración

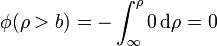
$\phi(\rho>b) = -\int_\infty^\rho 0\,\mathrm{d}\rho = 0$

Para $b > ρ > a$ , la integral se compone de dos tramos: uno por el exterior del cilindro, en el que el campo es nulo, y uno en la corona cilíndrica

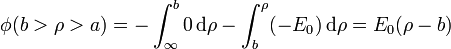
$\phi(b>\rho>a) = -\int_\infty^b 0\,\mathrm{d}\rho -\int_b^\rho (-E_0)\,\mathrm{d}\rho= E_0(\rho-b)$

Para 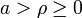$a> \rho \geq 0$ , debemos incluir tres tramos: uno por el exterior del cilindro, en el que el campo es nulo; uno en la corona cilíndrica; y otro en el cilindro interior

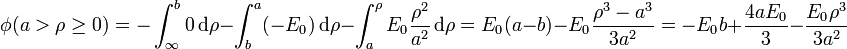
$\phi(a>\rho\geq 0) = -\int_\infty^b 0\,\mathrm{d}\rho -\int_b^a (-E_0)\,\mathrm{d}\rho-\int_a^\rho E_0\frac{\rho^2}{a^2}\,\mathrm{d}\rho= E_0(a-b)-E_0\frac{\rho^3-a^3}{3a^2} = -E_0b+\frac{4aE_0}{3}-\frac{E_0\rho^3}{3a^2}$

Reuniendo los tres resultados

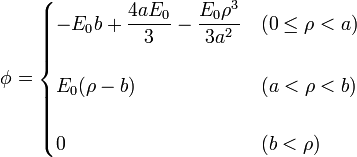
$\phi=\begin{cases} \displaystyle -E_0b+\frac{4aE_0}{3}-\frac{E_0\rho^3}{3a^2} & (0\leq\rho<a)\\ & \\ \displaystyle E_0(\rho-b) & (a<\rho< b) \\ & \\ 0 & (b<\rho)\end{cases}$

2.3 Energía electrostática

Este apartado también se puede realizar independientemente de los dos anteriores, calculando la energía electrostática a partir del campo eléctrico como

$U_\mathrm{e} = \int \frac{1}{2}\varepsilon_0 E^2\,\mathrm{d}\tau$

No obstante, también se puede hacer, aunque es más complicado, combinando los dos apartados anteriores y hallando la energía como

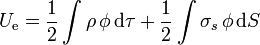
$U_\mathrm{e}= \frac{1}{2}\int \rho\,\phi\,\mathrm{d}\tau+\frac{1}{2}\int \sigma_s \,\phi\,\mathrm{d}S$

Veremos los dos métodos, comenzando por el más sencillo.

2.3.1 A partir del campo eléctrico

debemos integrar la densidad de energía electrostática en todo el espacio comprendido entre los dos planos $z = 0$ y $z = h$

$U_\mathrm{e}=\frac{\varepsilon_0}{2}\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\int_0^\infty\mathrm{d}\rho\, \rho\,E^2$

Esta integral se compone de tres términos: uno para el cilindro interior, uno para la corona cilíndrica y uno para el exterior.

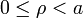En el cilindro interior ( $0\leq \rho<a$ )

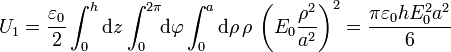
$U_1 = \frac{\varepsilon_0}{2}\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\int_0^a\mathrm{d}\rho\,\rho\,\left(E_0\frac{\rho^2}{a^2}\right)^2 = \frac{\pi\varepsilon_0hE_0^2a^2}{6}$

En la corona cilíndrica ( $a < ρ < b$ )

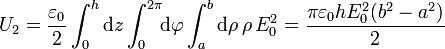
$U_2 = \frac{\varepsilon_0}{2}\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\int_a^b\mathrm{d}\rho\,\rho\,E_0^2 = \frac{\pi\varepsilon_0hE_0^2(b^2-a^2)}{2}$

En el exterior ( $b < ρ$ )

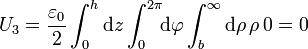
$U_3 = \frac{\varepsilon_0}{2}\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\int_b^\infty\mathrm{d}\rho\,\rho\,0 = 0$

Sumando las tres contribuciones

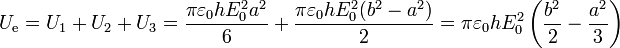
$U_\mathrm{e}=U_1+U_2+U_3 = \frac{\pi\varepsilon_0hE_0^2a^2}{6}+\frac{\pi\varepsilon_0hE_0^2(b^2-a^2)}{2} = \pi\varepsilon_0hE_0^2\left(\frac{b^2}{2}-\frac{a^2}{3}\right)$

2.3.2 A partir de las cargas y el potencial

Esta misma energía se puede calcular a partir de la integral

Por este método tenemos cuatro contribuciones

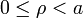De la carga de volumen en el cilindro ( $0\leq \rho < a$ )

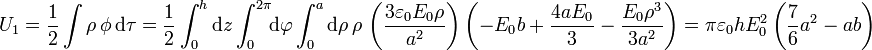
$U_1 = \frac{1}{2}\int\rho\,\phi\,\mathrm{d}\tau=\frac{1}{2}\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\int_0^a\mathrm{d}\rho\,\rho\,\left(\frac{3\varepsilon_0E_0\rho}{a^2}\right)\left(-E_0b+\frac{4aE_0}{3}-\frac{E_0\rho^3}{3a^2}\right)=\pi\varepsilon_0hE_0^2\left(\frac{7}{6}a^2-ab\right)$

De la carga superficial en la superficie $ρ = a$ . En esta superficie

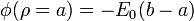
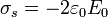
$\phi(\rho=a) = -E_0(b-a)\,$ $\sigma_s=-2\varepsilon_0E_0\,$

y la contribución a la energía es

$U_2 = \frac{1}{2}\int\sigma_s\,\phi\,\mathrm{d}S=\frac{1}{2}\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\,a\,\left(-2\varepsilon_0E_0\right)\left(-E_0(b-a)\right)=\pi\varepsilon_0hE_0^2\left(2ab-2a^2\right)$

De la carga de volumen en la corona cilíndrica ( $a < ρ < b$ )

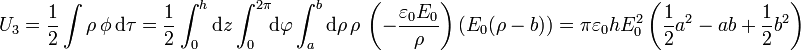
$U_3 = \frac{1}{2}\int\rho\,\phi\,\mathrm{d}\tau=\frac{1}{2}\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\int_a^b\mathrm{d}\rho\,\rho\,\left(-\frac{\varepsilon_0E_0}{\rho}\right)\left(E_0(\rho-b)\right)=\pi\varepsilon_0hE_0^2\left(\frac{1}{2}a^2-ab+\frac{1}{2}b^2\right)$

De la carga superficial en la superficie $ρ = b$ . En esta superficie

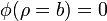
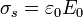
$\phi(\rho=b) = 0\,$ $\sigma_s=\varepsilon_0E_0\,$

y la contribución a la energía es

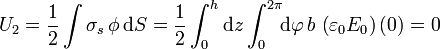
$U_2 = \frac{1}{2}\int\sigma_s\,\phi\,\mathrm{d}S=\frac{1}{2}\int_0^h\mathrm{d}z\int_0^{2\pi}\!\!\mathrm{d}\varphi\,b\,\left(\varepsilon_0E_0\right)\left(0\right)=0$

Sumando los cuatro términos

$U_\mathrm{e}= U_1+U_2+U_3+U_4 = =\pi\varepsilon_0hE_0^2\left(\frac{7}{6}a^2-ab+2ab-2a^2+\frac{1}{2}a^2-ab+\frac{1}{2}b^2\right)= \pi\varepsilon_0hE_0^2\left(\frac{1}{2}b^2-\frac{1}{3}a^2\right)$

El resultado es, naturalmente, el mismo que antes, pese a que las contibuciones individuales de cada región del espacio sean diferentes en uno y otro método. Esto ilustra la idea de que la energía electrostática no está realmente localizada en un punto concreto, sino que solo su total tiene sentido.

Campo eléctrico con simetría cilíndrica

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Distribuciones de carga

2.1.1 Distribución volumétrica

2.1.2 Distribución superficial

2.1.3 Carga total

2.2 Potencial eléctrico

2.3 Energía electrostática

2.3.1 A partir del campo eléctrico

2.3.2 A partir de las cargas y el potencial

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES