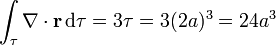Divergencia de un campo vectorial

De Laplace

1 Introducción

2 Definición

Se define la divergencia de un campo vectorial $\mathbf{A}$ en un punto $\mathbf{r}_0$ como el límite

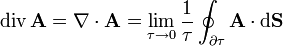
$\mathrm{div}\,\mathbf{A}=\nabla\cdot\mathbf{A}=\lim_{\tau\to 0}\frac{1}{\tau} \oint_{\partial\tau}\mathbf{A}\cdot\mathrm{d}\mathbf{S}$

donde el límite se toma sobre volúmenes $τ$ cada vez más pequeños que tienden al punto $\mathbf{r}_0$

La divergencia de un campo vectorial es una cantidad escalar.

Esta cantidad es independiente de la sucesión de volúmenes que se tomen con tal de que converjan en el mismo punto de manera uniforme.

2.1 Ejemplo

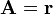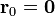Vamos a calcular la divergencia de $\mathbf{A}=\mathbf{r}$ en $\mathbf{r}_0 = \mathbf{0}$ .

En el artículo sobre flujo de un campo vectorial se ve que si consideramos una superficie cúbica de arista $2 a$ en torno al origen de coordenadas, el flujo del vector de posición a través de esta superficie es

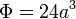
$\Phi = 24 a^3\,$

El volumen de este cubo es

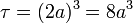
$\tau = (2a)^3 = 8a^3\,$

Por tanto la divergencia en 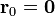$\mathbf{r}_0 = \mathbf{0}$ es

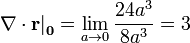
$\left.\nabla\cdot\mathbf{r}\right|_{\mathbf{0}} = \lim_{a\to 0 }\frac{24a^3}{8a^3} = 3$

Calculemos ahora esta misma divergencia pero considerando esferas de radio $R$ en torno al origen. Para cada una de estas esferas el volumen es

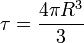
$\tau = \frac{4\pi R^3}{3}$

y el flujo a través de la superficie esférica

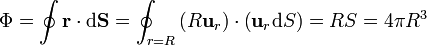
$\Phi = \oint \mathbf{r}\cdot\mathrm{d}\mathbf{S}= \oint_{r=R} \left(R\mathbf{u}_r\right)\cdot\left(\mathbf{u}_r\mathrm{d}S\right) = RS = 4\pi R^3$

por lo que la divergencia en 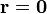$\mathbf{r}=\mathbf{0}$ es

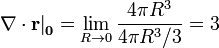
$\left.\nabla\cdot\mathbf{r}\right|_{\mathbf{0}} = \lim_{R\to 0}\frac{4\pi R^3}{4\pi R^3/3} = 3$

Vemos que el resultado es independiente de que lo hayamos calculado usando cubos o esferas.

Hay que destacar que lo que hemos calculado es la divergencia en un solo punto.

3 Fuentes escalares de un campo vectorial

La divergencia es una cantidad escalar con signo. Este signo posee significado geométrico y físico:

Si la divergencia de un campo vectorial en un punto es positiva, quiere decir que en dicho punto el campo radia hacia el exterior. Se dice que esa posición el campo vectorial posee un manantial.

Si por contra la divergencia es negativa, el campo converge hacia dicho punto; se dice que el campo posee un sumidero.

Ambos, manantiales y sumideros, constituyen las fuentes escalares de un campo vectorial; por ello

Si la divergencia es nula en un punto el campo carece de fuentes escalares en dicho punto.

El concepto de divergencia se define para cada punto. A partir de esta definición, puede construirse un campo escalar a partir de uno vectorial, cuyo valor es igual a la divergencia del campo vectorial en dicho punto

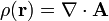
$\rho(\mathbf{r})=\nabla\cdot\mathbf{A}$

Este campo $ρ$ , que rescribe la distribución de manantiales y sumideros del campo vectorial, se conoce como fuentes escalares de $\mathbf{A}$ .

El uso de la palabra fuentes para algo que parece derivarse de otra cosa, se debe a que en la práctica el camino es el contrario: lo que se conoce habitualmente son las fuentes del campo y la cantidad que hay que calcular es el propio campo vectorial. En este sentido las fuentes “producen” el campo.

El ejemplo físico más sencillo es el del campo electrostático. Las cargas eléctricas (que son las fuentes escalares) producen el campo eléctrico. El campo eléctrico radia hacia el exterior de las cargas positivas, que son sus manantiales, y converge hacia las cargas negativas, que son sus sumideros.

4 Campo solenoidal

Artículo completo: Campo solenoidal

Un campo cuyas fuentes escalares son nulas en todos los puntos del espacio

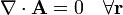
$\nabla\cdot\mathbf{A} = 0\quad \forall \mathbf{r}$

se denomina campo solenoidal.

El ejemplo más importante, en electromagnetismo, de campo solenoidal es el campo magnético \mathbf{B}, que verifica

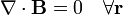
$\nabla\cdot\mathbf{B} = 0\quad \forall \mathbf{r}$

tanto en situaciones estáticas como dinámicas.

Un campo solenoidal se caracteriza porque sus líneas de campo no pueden converger ni divergir de ningún punto; no pueden tener extremos localizados. Esto hace que las líneas solo puedan

ser cerradas, o
ir del infinito al infinito, o
dar vueltas sobre sí mismas, sin llegar a cerrarse, como en una madeja.

Un ejemplo analítico de campo solenoidal es

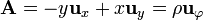
$\mathbf{A} = -y\mathbf{u}_x+x\mathbf{u}_y = \rho\mathbf{u}_\varphi$

Las líneas de campo de este campo vectorial describen circunferencias en torno al eje $Z$ , en acuerdo con la idea de que no tienen extremos.

Otro campo ligeramente diferente del anterior, pero también solenoidal, es

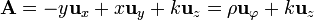
$\mathbf{A} = -y\mathbf{u}_x+x\mathbf{u}_y + k \mathbf{u}_z= \rho\mathbf{u}_\varphi+k\mathbf{u}_z$

cuyas líneas de campo son hélices en torno al eje $Z$ .

5 Expresión de la divergencia

Artículo completo: Expresión de la divergencia

La definición de la divergencia a partir de un límite, aunque rigurosa, es poco práctica. En particular, si lo que deseamos es calcular las fuentes escalares de un campo vectorial, necesitamos una expresión del límite válido para todos y cada uno de los puntos del espacio, lo cual puede ser extremadamente complicado.

Afortunadamente, la divergencia puede calcularse como una combinación de derivadas parciales.

5.1 En coordenadas cartesianas

En coordenadas cartesianas la expresión de la divergencia es la más sencilla posible:

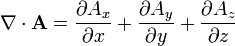
$\nabla\cdot\mathbf{A}=\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z}$

5.1.1 Ejemplos

Consideremos el campo vectorial

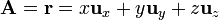
$\mathbf{A} = \mathbf{r}=x\mathbf{u}_x+y\mathbf{u}_y+z\mathbf{u}_z$

Su divergencia, calculada en cartesianas, es

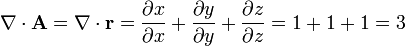
$\nabla\cdot\mathbf{A} = \nabla\cdot\mathbf{r} = \frac{\partial x}{\partial x}+\frac{\partial y}{\partial y}+\frac{\partial z}{\partial z} = 1+1+1 = 3$

Este parece el mismo resultado que obtuvimos antes, pero es mucho más que eso. En el cálculo anterior hallamos la divergencia exclusivamente en el origen de coordenadas. Ahora la hemos calculado para todos los puntos del espacio, resultando un valor positivo y constante para todo el espacio.

Esto quiere decir que, aunque las líneas de campo radian solo desde el origen, si consideramos un elemento de volumen en torno a un punto arbitrario del espacio, la cantidad de campo que sale del elemento es mayor que la que entra en él.

Podemos comprobar también cómo

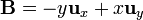
$\mathbf{B}=-y\mathbf{u}_x+x\mathbf{u}_y$

es un campo solenoidal. Hallando su divergencia en cartesianas

$\nabla\cdot\mathbf{B} = \frac{\partial(-y)}{\partial x}+\frac{\partial x}{\partial y}+\frac{\partial 0}{\partial z} = 0+0+0 = 0$

5.2 En coordenadas cilíndricas

La expresión correspondiente para la divergencia calculada en coordenadas cilíndricas es un poco más complicada que en cartesianas

$\nabla\cdot\mathbf{A}=\frac{1}{\rho}\,\frac{\partial\ }{\partial \rho}\left(\rho A_\rho\right)+\frac{1}{\rho}\,\frac{\partial A_\varphi}{\partial \varphi}+\frac{\partial A_z}{\partial z}$

5.2.1 Ejemplos

La divergencia del vector de posición,

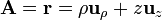
$\mathbf{A}=\mathbf{r}=\rho\mathbf{u}_\rho+z\mathbf{u}_z$

calculada en coordenadas cilíndricas nos da

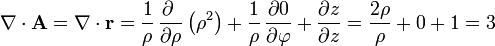
$\nabla\cdot\mathbf{A}=\nabla\cdot\mathbf{r}=\frac{1}{\rho}\,\frac{\partial\ }{\partial \rho}\left(\rho^2\right)+\frac{1}{\rho}\,\frac{\partial 0}{\partial \varphi}+\frac{\partial z}{\partial z}=\frac{2\rho}{\rho}+0+1 = 3$

que naturalmente coincide con el resultado obtenido empleando cartesianas.

Para el campo $\mathbf{B}$ definido anteriormente

$\mathbf{B}=-y\mathbf{u}_x+x\mathbf{u}_y = \rho\mathbf{u}_\varphi$

la divergencia resulta

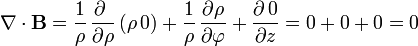
$\nabla\cdot\mathbf{B}=\frac{1}{\rho}\,\frac{\partial\ }{\partial \rho}\left(\rho\,0\right)+\frac{1}{\rho}\,\frac{\partial \rho}{\partial \varphi}+\frac{\partial\,0}{\partial z} = 0+0+0 = 0$

5.3 En coordenadas esféricas

La expresión correspondiente en esféricas es considerablemente más complicada que las dos anteriores

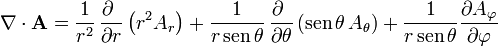
$\nabla\cdot\mathbf{A}=\frac{1}{r^2}\,\frac{\partial\ }{\partial r}\left(r^2 A_r\right)+\frac{1}{r\,\mathrm{sen}\,\theta}\,\frac{\partial\ }{\partial \theta}\left(\mathrm{sen}\,\theta\,A_\theta\right)+\frac{1}{r\,\mathrm{sen}\,\theta}\frac{\partial A_\varphi}{\partial \varphi}$

5.3.1 Ejemplos

La divergencia del vector de posición,

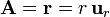
$\mathbf{A}=\mathbf{r}=r\,\mathbf{u}_r$

calculada en coordenadas esféricas es

$\nabla\cdot\mathbf{A}=\nabla\cdot\mathbf{r}=\frac{1}{r^2}\,\frac{\partial\ }{\partial r}\left(r^3\right)+\frac{1}{r\,\mathrm{sen}\,\theta}\,\frac{\partial\ }{\partial \theta}\left(\mathrm{sen}\,\theta\,0\right)+\frac{1}{r\,\mathrm{sen}\,\theta}\frac{\partial 0}{\partial \varphi}=\frac{3r^2}{r^2}+0+0=3$

Para el campo $\mathbf{B}$ definido anteriormente

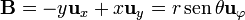
$\mathbf{B}=-y\mathbf{u}_x+x\mathbf{u}_y = r\,\mathrm{sen}\,\theta\mathbf{u}_\varphi$

la divergencia resulta

$\nabla\cdot\mathbf{B}=\frac{1}{r^2}\,\frac{\partial\ }{\partial r}\left(r^20\right)+\frac{1}{r\,\mathrm{sen}\,\theta}\,\frac{\partial\ }{\partial \theta}\left(\mathrm{sen}\,\theta\,0\right)+\frac{1}{r\,\mathrm{sen}\,\theta}\frac{\partial\ }{\partial \varphi}\left(r\,\mathrm{sen}\,\theta\right)=0+0+0=0$

5.4 En un sistema ortogonal arbitrario

La expresión general para la divergencia en un sistema de coordenadas ortogonales 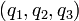$(q_1,q_2,q_3)\,$ es

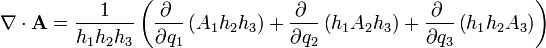
$\nabla\cdot\mathbf{A} = \frac{1}{h_1h_2h_3}\left(\frac{\partial\ }{\partial q_1}\left(A_1h_2h_3\right)+\frac{\partial\ }{\partial q_2}\left(h_1A_2h_3\right)+\frac{\partial\ }{\partial q_3}\left(h_1h_2A_3\right)\right)$

donde $h 1$ , $h 2$ y $h 3$ son los factores de escala del sistema de coordenadas.

Es sencillo comprobar que esta fórmula conduce a las tres anteriores para los sistemas de coordenadas más usuales, haciendo

Cartesianas: $h x = h x = h z = 1$
Cilíndricas: $h ρ = 1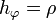$ , $h_\varphi=\rho$ , $h z = 1$
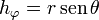
Esféricas: $h r = 1$ , $h θ = r$ , $h_\varphi = r\,\mathrm{sen}\,\theta$

6 La divergencia y el operador nabla

La notación de la divergencia de un campo vectorial, como la aplicación del operador nabla en forma de producto escalar por el campo vectorial, está bien elegida, ya que la divergencia puede calcularse realizando literalmente esta operación. Esto es evidente en coordenadas cartesianas:

$\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z}=\left(\mathbf{u}_x\frac{\partial\ }{\partial x}+\mathbf{u}_y\frac{\partial\ }{\partial y}+\mathbf{u}_z\frac{\partial \ }{\partial z}\right)\cdot\left(A_x\mathbf{u}_x+A_y\mathbf{u}_y+A_z\mathbf{u}_z\right)=\nabla\cdot\mathbf{A}$

Lo mismo es cierto en cualquier otro sistema de coordenadas (ya que tanto el operador nabla como los campos vectoriales son entes independientes del sistema que se use para representarlos). Sin embargo, para sistemas curvilíneos es necesario ser precavido con los vectores de la base. Por ejemplo, en coordenadas cilíndricas tenemos que

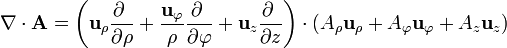
$\nabla\cdot\mathbf{A}=\left(\mathbf{u}_\rho\frac{\partial\ }{\partial\rho}+\frac{\mathbf{u}_\varphi}{\rho}\frac{\partial\ }{\partial\varphi}+\mathbf{u}_z\frac{\partial\ }{\partial z}\right)\cdot\left(A_\rho\mathbf{u}_\rho+A_\varphi\mathbf{u}_\varphi+A_z\mathbf{u}_z\right)$

pero a la hora de aplicar el operador nabla debemos tener en cuenta que

Los vectores de la base dependen de la posición

y por tanto deben ser incluidos en la derivación, lo que implica la aparición de nuevos términos en el producto escalar

$\nabla\cdot\mathbf{A}=\frac{\partial A_\rho}{\partial\rho}+\frac{1}{\rho}\,\frac{\partial A_\varphi}{\partial\varphi}+\frac{\partial A_z}{\partial z}+A_\rho\mathbf{u}_\rho\cdot\frac{\partial\mathbf{u}_\rho}{\rho}+ A_\varphi\mathbf{u}_\varphi\cdot\frac{\partial\mathbf{u}_\varphi}{\rho}+\cdots$

tenemos que

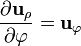
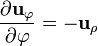
$\frac{\partial\mathbf{u}_\rho}{\partial\varphi} = \mathbf{u}_\varphi$ $\frac{\partial\mathbf{u}_\varphi}{\partial\varphi} = -\mathbf{u}_\rho$

y el resto de las derivadas de los vectores de la base son nulas. Sustituyendo esto en la expresión completa queda

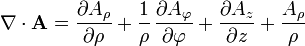
$\nabla\cdot\mathbf{A}=\frac{\partial A_\rho}{\partial\rho}+\frac{1}{\rho}\,\frac{\partial A_\varphi }{\partial\varphi}+\frac{\partial A_z}{\partial z}+\frac{A_\rho}{\rho}$

que equivale a la expresión de la divergencia en cilíndricas que dimos antes.

6.1 Divergencia de una suma y un producto

6.1.1 Suma

El operador nabla es lineal, y también lo es el producto escalar, por ello, la divergencia de la suma es igual a la suma de las divergencias

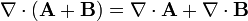
$\nabla\cdot\left(\mathbf{A}+\mathbf{B}\right) = \nabla\cdot\mathbf{A}+\nabla\cdot\mathbf{B}$

6.1.2 Producto

La divergencia solo actúa sobre campos vectoriales. Por ello, a la hora de hablar de productos sólo hay que considerar aquellos que den como resultado un vector. Estos son, el producto de un campo escalar por uno vectorial y el producto vectorial de dos vectores.

Para el caso de un producto de un campo escalar por uno vectorial, la expresión de la divergencia es análoga a la de la derivada de un producto:

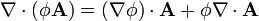
$\nabla\cdot\left(\phi\mathbf{A}\right) = (\nabla\phi)\cdot\mathbf{A} + \phi \nabla\cdot\mathbf{A}$

o, dicho en palabras: “la divergencia de un campo escalar por un campo vectorial es igual al gradiente del escalar, multiplicado escalarmente por el vector, más el escalar multiplicado escalarmente por la divergencia del vector”. Obsérvese que es el gradiente del campo escalar, no su divergencia, que no existe.

El segundo caso, del producto vectorial de dos campos vectoriales, requiere el uso del rotacional

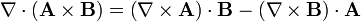
$\nabla\cdot(\mathbf{A}\times\mathbf{B}) = \left(\nabla\times\mathbf{A}\right)\cdot\mathbf{B} - (\nabla\times\mathbf{B})\cdot\mathbf{A}$

la aparición del signo menos en el segundo término se debe a que se ha invertido el orden de los dos vectores, cambiando el signo del producto vectorial.

7 Teorema de Gauss

Artículo completo: Teorema de Gauss

El flujo de un campo a través de una superficie cerrada y la divergencia están estrechamente relacionados a través del Teorema de Gauss

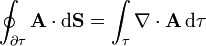
$\oint_{\partial\tau} \mathbf{A}\cdot\mathrm{d}\mathbf{S} = \int_\tau \nabla\cdot\mathbf{A}\,\mathrm{d}\tau$

que nos dice que la cantidad de campo que escapa hacia el exterior de una superficie cerrada $\partial\tau$ es igual a la suma neta de las fuentes escalares contenidas en el interior de dicha superficie.

7.1 Interpretación física

Según hemos dicho antes, la divergencia puede entenderse como la densidad de fuentes de un campo vectorial, siendo positiva si el campo posee un manantial y negativa si tiene un sumidero. Por ejemplo, en el caso del flujo de calor 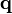$\mathbf{q}$ , los manantiales representan la producción de calor y los sumideros su consumo.

La integral de volumen de la divergencia

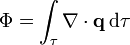
$\Phi = \int_\tau \nabla\cdot\mathbf{q}\,\mathrm{d}\tau$

será la suma de todas las fuentes que hay en el interior del volumen. Teniendo en cuenta el signo, el resultado será igual a la producción de todos los manantiales, menos el consumo en los sumideros, esto es, la producción neta de calor en el volumen. Si se produce más calor del que se consume, ese calor extra debe escapar al exterior del volumen. Esa emisión al exterior es lo que representa el flujo

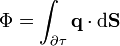
$\Phi = \int_{\partial\tau} \mathbf{q}\cdot\mathrm{d}\mathbf{S}$

Por tanto, lo que nos dice el teorema de Gauss es que lo que escapa hacia el exterior equivale a la producción neta en el interior del volumen.

7.2 Ejemplo

Consideremos el flujo del campo 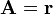$\mathbf{A}=\mathbf{r}$ a través de las paredes de un cubo de lado $2 a$ , centrado en el origen y con aristas paralelas a los ejes. El flujo a través de sus caras, tal como se ve en el artículo sobre flujo de un campo vectorial es

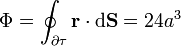
$\Phi = \oint_{\partial\tau} \mathbf{r}\cdot\mathrm{d}\mathbf{S} = 24a^3$

Por otro lado, la divergencia del vector de posición, según hemos visto, es

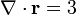
$\nabla\cdot\mathbf{r} = 3$

y su integral de volumen

$\int_\tau \nabla\cdot\mathbf{r}\,\mathrm{d}\tau = 3\tau = 3(2a)^3 = 24a^3$

Divergencia de un campo vectorial

De Laplace

Contenido

1 Introducción

2 Definición

2.1 Ejemplo

3 Fuentes escalares de un campo vectorial

4 Campo solenoidal

5 Expresión de la divergencia

5.1 En coordenadas cartesianas

5.1.1 Ejemplos

5.2 En coordenadas cilíndricas

5.2.1 Ejemplos

5.3 En coordenadas esféricas

5.3.1 Ejemplos

5.4 En un sistema ortogonal arbitrario

6 La divergencia y el operador nabla

6.1 Divergencia de una suma y un producto

6.1.1 Suma

6.1.2 Producto

7 Teorema de Gauss

7.1 Interpretación física

7.2 Ejemplo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES