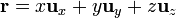Coordenadas cartesianas. Base vectorial

De Laplace

Contenido

1 Vectores de la base
2 Base ortonormal dextrógira
3 Factores de escala
4 Vector de posición
5 Enlaces

1 Vectores de la base

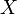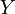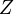Para el sistema cartesiano la construcción es inmediata. En cada punto del espacio las líneas coordenadas son rectas paralelas a los ejes $X\,$ , $Y\,$ y $Z\,$ . Por tanto, los vectores de la base cartesiana son nuestros viejos conocidos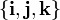 $\{\mathbf{i}, \mathbf{j}, \mathbf{k}\}\,$

$\mathbf{u}_x = \mathbf{i}\qquad \mathbf{u}_y = \mathbf{j}\qquad \mathbf{u}_z = \mathbf{k}$

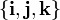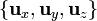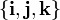con una diferencia de matiz. La base $\{\mathbf{i}, \mathbf{j}, \mathbf{k}\}\,$ no está asociada a un punto en concreto. La base $\{\mathbf{u}_x, \mathbf{u}_y, \mathbf{u}_z\}$ sí está asociada a cada punto en concreto, sólo que en cada punto coincide con $\{\mathbf{i}, \mathbf{j}, \mathbf{k}\}\,$ .

2 Base ortonormal dextrógira

Los vectores de la base cartesiana forman una base ortonormal dextrógira si las coordenadas se ordenan en la forma tradicional 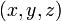$(x,y,z)\,$ . Los productos escalares y vectoriales vienen dados por las siguientes tablas de multiplicar

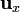
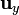
·	$\mathbf{u}_x$	$\mathbf{u}_y$	$\mathbf{u}_z$
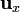
$\mathbf{u}_x$	1	0	0
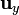
$\mathbf{u}_y$	0	1	0
$\mathbf{u}_z$	0	0	1

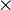
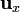
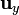
$\times\,$	$\mathbf{u}_x$	$\mathbf{u}_y$	$\mathbf{u}_z$
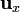
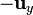
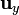
$\mathbf{u}_x$	0	$\mathbf{u}_z$	$-\mathbf{u}_y$
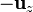
$\mathbf{u}_y$	$-\mathbf{u}_z$	0	$\mathbf{u}_x$
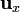
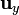
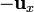
$\mathbf{u}_z$	$\mathbf{u}_y$	$-\mathbf{u}_x$	0

3 Factores de escala

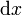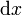Los factores de escala en este sistema también son sencillos. Puesto que las coordenadas representan distancias a los planos coordenados, si nos desplazamos una cantidad $\mathrm{d}x\,$ a lo largo de la línea coordenada $x\,$ , la distancia que recorremos es... ¡ $\mathrm{d}x\,$ !. Lo mismo con 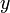$y\,$ y con $z\,$ . Por tanto, los factores de escala para las tres coordenadas valen