Entrar Página Discusión Historial Go to the site toolbox

Una esfera conductora rellena de una densidad de carga

De Laplace

Contenido

1 Enunciado

Una superficie esférica conductora de radio R, puesta a tierra, contiene en su interior una distribución de carga no uniforme, cuya densidad de carga es de la forma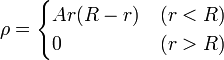
\rho =\begin{cases}A r(R-r) & (r< R) \\ 0 & (r>R)\end{cases}
  1. Calcule el campo eléctrico en todos los puntos del espacio.
  2. Calcule el valor de la carga almacenada en la esfera conductora.
  3. Halle el potencial eléctrico en el centro de la esfera.
    1. A partir del campo eléctrico.
    2. Por integración directa a partir de las densidades de carga.
  4. Halle la energía electrostática almacenada en el sistema.

2 Campo eléctrico

Al haber una superficie conductora a tierra, que funciona como Jaula de Faraday, el problema se desacopla en dos independientes: el exterior de la esfera y el interior de ella.

2.1 En el exterior de la esfera

En el exterior del conductor se verifica la ecuación de Laplace, puesto que no hay carga exterior

\nabla^2\phi =0    (r > R)

con las condiciones

\phi = 0\qquad(r=R)        \phi\to 0\qquad (r\to\infty)

La solución de la ecuación de Laplace en una región cuando el potencial se anula en todos los puntos de la frontera es simplemente

\phi = 0\qquad (r>R)   \Rightarrow   \mathbf{E}=-\nabla\phi = \mathbf{0}\qquad (r>R)

Dicho en términos físicos, la esfera conductora apantalla la densidad de carga interior, con el resultado de que en el exterior no se percibe campo alguno.

2.2 En el interior de la esfera

En el interior, dada la simetría rotacional de la distribución de carga, la herramienta natural para calcular el campo es la ley de Gauss en forma integral.

Por la simetría del sistema, el campo va a ser radial y con módulo dependiente sólo de la distancia al origen

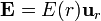
\mathbf{E} = E(r)\mathbf{u}_r\,

Por ello, si consideramos el flujo del campo a través de una superficie esférica de radio r concéntrica con la esfera conductora

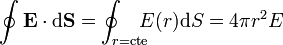
\oint \mathbf{E}\cdot\mathrm{d}\mathbf{S} = \oint_{r=\mathrm{cte}}\!\!\!\! E(r)\mathrm{d}S = 4\pi r^2E

De acuerdo con la ley de Gauss, este flujo será igual a la carga encerrada en esta superficie esférica, dividida por \varepsilon_0

\oint \mathbf{E}\cdot\mathrm{d}\mathbf{S} = \frac{Q_\mathrm{int}(r)}{\varepsilon_0} = \frac{1}{\varepsilon_0}\int_{r'<r}\rho(r')\,\mathrm{d}\tau'

La carga encerrada por una esfera de radio r es

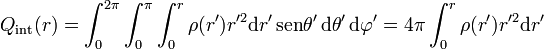
Q_\mathrm{int}(r) = \int_0^{2\pi}\int_0^\pi \int_0^r \rho(r')r'^2\mathrm{d}r'\,\mathrm{sen}\theta'\,\mathrm{d}\theta'\,\mathrm{d}\varphi' = 4\pi \int_0^r\rho(r')r'^2\mathrm{d}r'

Sustituyendo la expresión de ρ(r)

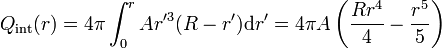
Q_\mathrm{int}(r) = 4\pi \int_0^r A r'^3(R-r')\mathrm{d}r' = 4\pi A\left(\frac{Rr^4}{4}-\frac{r^5}{5}\right)

Por tanto el campo eléctrico en el interior de la esfera vale

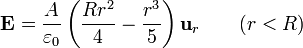
\mathbf{E} = \frac{A}{\varepsilon_0}\left(\frac{Rr^2}{4}-\frac{r^3}{5}\right)\mathbf{u}_r\qquad(r<R)

Reuniendo los dos resultados

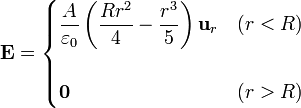
\mathbf{E}=\begin{cases}\displaystyle \frac{A}{\varepsilon_0}\left(\frac{Rr^2}{4}-\frac{r^3}{5}\right)\mathbf{u}_r & (r<R) \\ & \\ \mathbf{0} & (r>R)\end{cases}

3 Carga en la esfera conductora

Podemos calcular la carga en la superficie esférica conductora de dos formas: por aplicación del teorema de Faraday o integrando la densidad de carga superficial

3.1 Por el teorema de Faraday

Es una consecuencia inmediata de la ley de Gauss. Si calculamos el flujo del campo eléctrico a través de una superficie exterior al conductor, tenemos que

Q_\mathrm{int}(r>R) = \varepsilon_0\oint \mathbf{E}\cdot\mathrm{d}\mathbf{S} = \varepsilon_0\oint \mathbf{0}\cdot\mathrm{d}\mathbf{S} = 0

Por tanto la carga contenida dentro de esta superficie es nula. Esto quiere decir que la carga almacenada en la superficie conductora es exactamente igual y de signo contrario a la carga total almacenada en el volumen. Esta carga ya la hemos calculado en el apartado anterior. Basta sustituir r por R para obtener la carga total de volumen

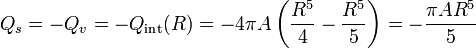
Q_s = -Q_v = -Q_\mathrm{int}(R) = -4\pi A \left(\frac{R^5}{4}-\frac{R^5}{5}\right) = -\frac{\pi A R^5}{5}

3.2 A partir de la densidad de carga superficial

El campo eléctrico es discontinuo en la superficie conductora, ya que en el exterior es nulo, mientras que en el interior no lo es. Esto quiere decir que en la esfera existe una densidad de carga superficial, proporcional al salto en el campo eléctrico

\sigma_s = \varepsilon_0 \mathbf{n}\cdot[\mathbf{E}] = \varepsilon_0\mathbf{u}_r\cdot\left(\mathbf{0}-\frac{A}{\varepsilon_0}\left(\frac{R^3}{4}-\frac{R^3}{5}\right)\mathbf{u}_r \right)= -\frac{AR^3}{20}

Esta densidad de carga es uniforme, por lo que la carga total es simplemente el producto de esta densidad por el área de la esfera

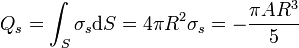
Q_s = \int_S \sigma_s\mathrm{d}S = 4\pi R^2 \sigma_s = -\frac{\pi AR^3}{5}

4 Potencial en el centro de la esfera

4.1 A partir del campo eléctrico

Una forma de hallar el potencial eléctrico en el centro de la esfera es integrando a lo largo de un camino que va desde el infinito hasta el centro

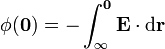
\phi(\mathbf{0}) = -\int_\infty^\mathbf{0}\mathbf{E}\cdot\mathrm{d}\mathbf{r}

Considerando un camino radial, tal que 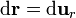\mathrm{d}\mathbf{r}=\mathrm{d}\mathbf{u}_r, esta integral se compone de dos tramos: uno por el exterior de la esfera y otro por su interior

\phi(\mathbf{0}) = -\int_\infty^R0\cdot\mathrm{d}r-\int_R^0\frac{A}{\varepsilon_0}\left(\frac{Rr^2}{4}-\frac{r^3}{5}\right)\mathrm{d}r = \frac{A}{\varepsilon_0}\left(\frac{R^4}{12}-\frac{R^4}{20}\right) = \frac{AR^4}{30\varepsilon_0}

4.2 Por integración directa

Otra posibilidad es emplear la expresión integral para el potencial eléctrico creado por una distribución de carga

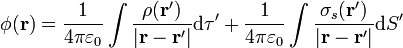
\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\int \frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}\tau'+\frac{1}{4\pi\varepsilon_0}\int \frac{\sigma_s(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}S'

donde hay que recordar que en este caso, además de la distribución de carga de volumen tenemos una carga en la superficie de la esfera conductora.

Como sólo deseamos el potencial en el centro de la esfera, 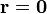\mathbf{r}=\mathbf{0}. La integral en el volumen es el producto de una integral sobre θ' y 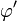\varphi' (que dan un factor 4π) y una integral radial:

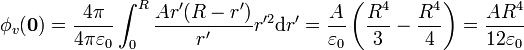
\phi_v(\mathbf{0}) = \frac{4\pi}{4\pi\varepsilon_0}\int_0^R \frac{Ar'(R-r')}{r'}r'^2\mathrm{d}r' = \frac{A}{\varepsilon_0}\left(\frac{R^4}{3}-\frac{R^4}{4}\right) = \frac{AR^4}{12\varepsilon_0}

La integral sobre la superficie simplemente produce un factor 4πR2, ya que el integrando no depende ni de θ' ni de 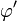\varphi'

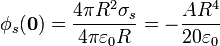
\phi_s(\mathbf{0}) = \frac{4\pi R^2 \sigma_s}{4\pi\varepsilon_0 R} = -\frac{AR^4}{20\varepsilon_0}

Sumando las dos contribuciones

\phi(\mathbf{0}) = \frac{AR^4}{12\varepsilon_0}-\frac{AR^4}{20\varepsilon_0} = \frac{AR^4}{30\varepsilon_0}

5 Energía electrostática almacenada

La forma más sencilla de calcular la energía electrostática almacenada en el sistema es a partir de la densidad de energía

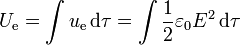
U_\mathrm{e} = \int u_\mathrm{e}\,\mathrm{d}\tau = \int \frac{1}{2}\varepsilon_0 E^2\,\mathrm{d}\tau

La integral se extiende a todo el espacio. Sin embargo, dado que el campo exterior es nulo, el cálculo se reduce a una integral en el volumen de la esfera. De nuevo, el integrando depende solo de r, por lo que la integral en las variables angulares da un factor 4π. La integral radial queda

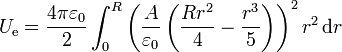
U_\mathrm{e} = \frac{4\pi\varepsilon_0}{2} \int_0^R \left(\frac{A}{\varepsilon_0}\left(\frac{Rr^2}{4}-\frac{r^3}{5}\right)\right)^2r^2\,\mathrm{d}r

Desarrollando el cuadrado

U_\mathrm{e} = \frac{2\pi A^2}{\varepsilon_0} \int_0^R \left(\frac{R^2r^6}{16}-\frac{Rr^7}{10}+\frac{r^8}{25}\right)\,\mathrm{d}r = \frac{2\pi A^2R^9}{\varepsilon_0}\left(\frac{1}{112}-\frac{1}{80}+\frac{1}{225}\right)=\frac{11\pi A^2R^9}{6300\varepsilon_0}
Obtenido de "http://tesla.us.es/wiki/index.php/Una_esfera_conductora_rellena_de_una_densidad_de_carga"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 19:37, 10 ene 2010. - Esta página ha sido visitada 56.730 veces. - Aviso legal - Acerca de Laplace