Potencial de dos cargas puntuales
De Laplace
1 Enunciado
Halle el potencial creado por dos cargas q1, − q2 situadas a una distancia a una de la otra. Demuestre que la superficie equipotencial V = 0 es una esfera.
2 Solución
El potencial creado por estas dos cargas en cualquier punto del espacio es
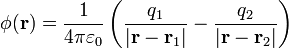
La equipotencial V=0 vendrá dada por la ecuación
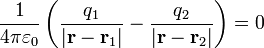
No es evidente que ésta sea la ecuación de una esfera. Para ponerlo de manifiesto reescribimos la ecuación como

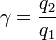
Supondremos, sin pérdida de generalidad, que γ < 1, esto es, que q2 es la menor en magnitud de las dos cargas.
Podemos tomar el origen de coordenadas en la carga q1 y el eje Z el que pasa por las dos cargas, de forma que 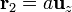 . Expresando el vector de posición en cartesianas esta ecuación queda
. Expresando el vector de posición en cartesianas esta ecuación queda
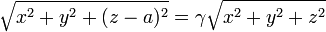
Elevando al cuadrado y agrupando términos

Esta es ya claramente la ecuación de una esfera. Para identificar su radio y la posición del centro, despejamos y competamos cuadrados
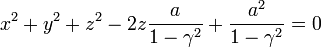
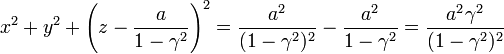
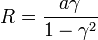
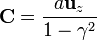
- Dado que
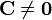 y
y 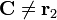 , la esfera no está centrada en ninguna de las dos cargas
, la esfera no está centrada en ninguna de las dos cargas
- Puesto que
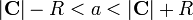 , esta esfera envuelve a la menor de las dos cargas, aunque no está centrada en ella.
, esta esfera envuelve a la menor de las dos cargas, aunque no está centrada en ella.
- Sólo la equipotencial V = 0 es una esfera. El resto de las equipotenciales tienen formas más complicadas, no esféricas.






