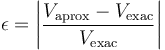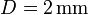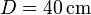Problemas de electrostática en el vacío
De Laplace
(→Potencial en el punto O) |
(→{{nivel|2}} Sistema electrostático de tres cargas puntuales) |
||
| (83 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | == | + | =={{nivel|1}} [[Modelo semiclásico del átomo de Bohr]]== |
Supongamos un protón y un electrón situados a una distancia de un radio de Bohr | Supongamos un protón y un electrón situados a una distancia de un radio de Bohr | ||
| Línea 7: | Línea 7: | ||
# Suponga que en lugar a una distancia de un radio de Bohr el protón se encuentra en el centro de la Tierra y el electrón en el centro de la Luna (a 384000 km), ¿cómo cambian las fuerzas eléctrica y gravitatoria? ¿Y el cociente entre ellas? De acuerdo con este resultado, ¿cómo se explica que la fuerza dominante en el sistema Tierra-Luna sea la gravedad? | # Suponga que en lugar a una distancia de un radio de Bohr el protón se encuentra en el centro de la Tierra y el electrón en el centro de la Luna (a 384000 km), ¿cómo cambian las fuerzas eléctrica y gravitatoria? ¿Y el cociente entre ellas? De acuerdo con este resultado, ¿cómo se explica que la fuerza dominante en el sistema Tierra-Luna sea la gravedad? | ||
| - | == | + | =={{nivel|1}} [[Electroscopio de dos hilos]]== |
Un electroscopio mide la carga por la desviación angular de dos esferas idénticas conductoras, suspendidas por cuerdas aislantes de masas despreciables y longitud <math>l</math>. Cada esfera tiene una masa <math>m</math> y está sometida a la gravedad <math>\mathbf{g}</math>. Las cargas pueden considerarse como puntuales e iguales entre sí. Halle la ecuación que liga el semiángulo <math>\theta</math> con el valor de la carga total <math>Q</math> depositada en las esferas. | Un electroscopio mide la carga por la desviación angular de dos esferas idénticas conductoras, suspendidas por cuerdas aislantes de masas despreciables y longitud <math>l</math>. Cada esfera tiene una masa <math>m</math> y está sometida a la gravedad <math>\mathbf{g}</math>. Las cargas pueden considerarse como puntuales e iguales entre sí. Halle la ecuación que liga el semiángulo <math>\theta</math> con el valor de la carga total <math>Q</math> depositada en las esferas. | ||
| Línea 13: | Línea 13: | ||
longitud del cable del que penden es 20 cm. Admita asimismo que los ángulos de desviación pueden medirse como mucho con una precisión de 1°. ¿Cuál es la carga mínima que puede medirse con este aparato? ¿Y la carga máxima? | longitud del cable del que penden es 20 cm. Admita asimismo que los ángulos de desviación pueden medirse como mucho con una precisión de 1°. ¿Cuál es la carga mínima que puede medirse con este aparato? ¿Y la carga máxima? | ||
| - | == | + | =={{nivel|1}} [[Tres cargas en un triángulo equilátero]]== |
Tres cargas <math>q_1</math>, <math>q_2</math> y <math>q_3</math>, se encuentran en los vértices de un triángulo equilátero de lado <math>a = 1\mathrm{cm}</math>. Determine la fuerza sobre cada carga cuando: | Tres cargas <math>q_1</math>, <math>q_2</math> y <math>q_3</math>, se encuentran en los vértices de un triángulo equilátero de lado <math>a = 1\mathrm{cm}</math>. Determine la fuerza sobre cada carga cuando: | ||
| Línea 21: | Línea 21: | ||
# <math>q_1=q_2=1\,\mu\mathrm{C}</math>, <math>q_3 = -2\,\mu\mathrm{C}</math>. | # <math>q_1=q_2=1\,\mu\mathrm{C}</math>, <math>q_3 = -2\,\mu\mathrm{C}</math>. | ||
| - | == | + | =={{nivel|1}} [[Cuatro cargas en un rectángulo]]== |
Una carga puntual <math>q_1 = 108\,\mathrm{nC}</math> se encuentra situada en el | Una carga puntual <math>q_1 = 108\,\mathrm{nC}</math> se encuentra situada en el | ||
| - | origen de coordenadas. En <math>x=25\,\mathrm{mm}</math>, <math>y=z=0</math> se halla una segunda carga <math>q_2</math>. En <math>x=16\,\mathrm{mm}</math>, <math>y=12\,\mathrm{mm}</math> se encuentra una tercera carga <math>q_3</math>. | + | origen de coordenadas. En <math>x=25\,\mathrm{mm}</math>, <math>y=z=0\,</math> se halla una segunda carga <math>q_2</math>. En <math>x=16\,\mathrm{mm}</math>, <math>y=12\,\mathrm{mm}</math> se encuentra una tercera carga <math>q_3</math>. |
Calcule el valor que deben tener <math>q_2</math> y <math>q_3</math> si, ocupando las´posiciones indicadas, se desea que sea nula la fuerza sobre una carga <math>q_4=10\,\mathrm{nC}</math> situada en <math>x=9\,\mathrm{mm}</math>, <math>y=-12\,\mathrm{mm}</math>, <math>z=0</math>. | Calcule el valor que deben tener <math>q_2</math> y <math>q_3</math> si, ocupando las´posiciones indicadas, se desea que sea nula la fuerza sobre una carga <math>q_4=10\,\mathrm{nC}</math> situada en <math>x=9\,\mathrm{mm}</math>, <math>y=-12\,\mathrm{mm}</math>, <math>z=0</math>. | ||
| - | == | + | =={{nivel|2}} [[Tres cargas en un anillo]]== |
| - | Se dispone de tres cargas, una de valor <math>Q</math> y las otras dos de valor <math>q</math>. Estas cargas se ensartan en un anillo circular de radio <math>R</math> sobre el cual pueden deslizar libremente. Determine la ecuación para los ángulos del triángulo que forman las tres cargas. ¿Cuál es la solución para los casos <math>Q\gg q</math>, <math>Q=q\,</math> y <math>Q\ll q</math> | + | Se dispone de tres cargas, una de valor <math>Q</math> y las otras dos de valor <math>q</math>. Estas cargas se ensartan en un anillo circular de radio <math>R</math> sobre el cual pueden deslizar libremente. Determine la ecuación para los ángulos del triángulo que forman las tres cargas. ¿Cuál es la solución para los casos <math>Q\gg q</math>, <math>Q=q\,</math> y <math>Q\ll q</math>? |
| - | == | + | =={{nivel|2}} [[Fuerza entre dos varillas colineales]]== |
| - | + | Calcule la fuerza entre dos varillas colineales, de longitudes <math>L_1</math> y <math>L_2</math>, que almacenan respectivamente cargas <math>Q_1</math> y <math>Q_2</math>, cuando sus extremos más próximos distan una cantidad <math>a</math>. | |
| - | + | <center>[[Imagen:varillascolineales1.png]]</center> | |
| - | + | =={{nivel|3}} [[Campo eléctrico de un segmento cargado]]== | |
| - | + | Sea un segmento rectilíneo de longitud <math>L</math>, sobre el cual existe una densidad de carga uniforme <math>\lambda</math>. | |
| - | + | ||
| - | ===[[Campo eléctrico entre dos varillas]] | + | Halle el campo eléctrico que produce en un punto arbitrario del espacio |
| - | Dos varillas rectilíneas de longitud <math>L</math> están situadas paralelamente a una distancia <math>D</math>. Las varillas poseen cargas <math>\pm Q</math> distribuidas uniformemente. | + | |
| + | * ¿A qué se reduce el campo en el plano central del segmento? | ||
| + | * Calcule el límite del campo del segmento para <math>L\to\infty</math>. | ||
| + | |||
| + | =={{nivel|2}} [[Fuerza entre dos hilos cargados]]== | ||
| + | Un cable formado por dos hilos paralelos produce un campo eléctrico similar al producido por dos líneas infinitas con densidad de carga <math>\lambda</math> y <math>-\lambda</math>, situadas a una distancia <math>D</math> una de la otra. | ||
| + | |||
| + | Halle la fuerza que uno de los hilos produce sobre un segmento de longitud <math>h</math> del otro hilo. | ||
| + | |||
| + | =={{nivel|3}} [[Campo eléctrico entre dos varillas]]== | ||
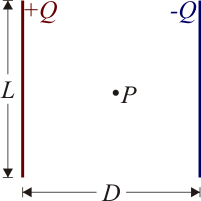
| + | [[Imagen:Dosvarillas.png|right]]Dos varillas rectilíneas de longitud <math>L</math> están situadas paralelamente a una distancia <math>D</math>. Las varillas poseen cargas <math>\pm Q</math> distribuidas uniformemente. | ||
# Halle aproximadamente el campo eléctrico en un punto <math>P</math> equidistante de ambas varillas, para el caso <math>D\gg L</math>. | # Halle aproximadamente el campo eléctrico en un punto <math>P</math> equidistante de ambas varillas, para el caso <math>D\gg L</math>. | ||
| Línea 49: | Línea 58: | ||
## <math>D=40\,\mathrm{cm}</math> | ## <math>D=40\,\mathrm{cm}</math> | ||
| - | == | + | =={{nivel|2}} [[Una varilla y una carga]]== |
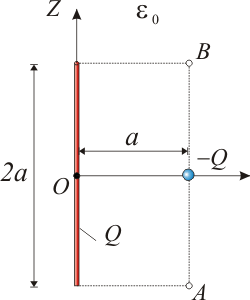
| - | + | [[Imagen:P2_i.gif|right]]Una carga eléctrica <math>Q</math> está uniformemente distribuida a lo largo de un segmento rectilíneo de longitud <math>2a</math>. A una distancia <math>a</math> del punto medio de dicho segmento y en dirección perpendicular a éste, se halla una carga puntual <math>-Q</math>. | |
| + | |||
| + | # Calcule el flujo del campo eléctrico a través de una superficie esférica de radio <math>a/2</math> centrada en el punto medio del segmento cargado (punto <math>O</math>). | ||
| + | # Obtenga la fuerza que actúa sobre la carga puntual. | ||
| + | # Calcule los momentos monopolar y dipolar de la distribución de carga descrita. Proponga expresiones aproximadas para el potencial y el campo eléctrico en puntos suficientemente alejados de la distribución. | ||
| + | # ¿Qué trabajo habría que realizar para mover la carga puntual entre los puntos <math>A</math> al <math>B</math>? (ver figura) | ||
| - | == | + | =={{nivel|2}} [[Campo eléctrico en el eje de un anillo|Campo en el eje de un anillo]]== |
| - | Halle el campo eléctrico en todos los puntos del eje de un anillo de radio | + | Halle el campo eléctrico en todos los puntos del eje de un anillo de radio <math>R</math> sobre el cual hay una densidad de carga uniforme <math>\lambda</math>. |
A partir de este resultado, calcule el campo creado por una corona circular de radios <math>R_1</math> y <math>R_2</math> (<math>R_1<R_2</math>), sobre la cual hay una densidad de carga uniforme <math>\sigma_0</math>, en los puntos de su eje. | A partir de este resultado, calcule el campo creado por una corona circular de radios <math>R_1</math> y <math>R_2</math> (<math>R_1<R_2</math>), sobre la cual hay una densidad de carga uniforme <math>\sigma_0</math>, en los puntos de su eje. | ||
| Línea 59: | Línea 73: | ||
¿A que se reduce si <math>R_1\to 0</math>? ¿Y si <math>R_2\to\infty</math>? Considere en particular el comportamiento en las proximidades de <math>z=0</math>. | ¿A que se reduce si <math>R_1\to 0</math>? ¿Y si <math>R_2\to\infty</math>? Considere en particular el comportamiento en las proximidades de <math>z=0</math>. | ||
| - | == | + | =={{nivel|3}} [[Campo de dos anillos coaxiales]]== |
| - | + | [[Imagen:2anilloscoaxiales.gif|right]]Dos anillos iguales de radio <math>R</math> y grosor despreciable están cargados eléctricamente con sendas distribuciones lineales y uniformes <math>+\lambda_0</math> y <math>-\lambda_0</math>. Los anillos se encuentran en planos paralelos separados una distancia <math>R</math>, pero con sus centros situados sobre el mismo eje. Tómese este eje como <math>Z</math>, y como origen de coordenadas <math>O</math> el punto medio entre los anillos. | |
| - | ===[[Campo debido a una | + | # Obtenga la expresión del potencial electrostático creado por estas distribuciones en los puntos del eje <math>Z</math>. Calcule el valor del potencial en un punto arbitrario del plano <math>XY</math>. |
| + | # Obtenga la expresión del campo eléctrico para los puntos del eje <math>Z</math>. ¿Cuánto vale la fuerza que actúa sobre una carga puntual <math>q</math> situada en O? ¿Qué trabajo se ha realizado para traer esta carga desde el infinito hasta este punto? | ||
| + | # Suponga que, en lugar de la carga puntual, se sitúa un dipolo eléctrico de momento dipolar <math>\mathbf{p}=p\mathbf{u}_z</math>, en el centro del anillo de carga positiva. Obtenga la expresión de la energía potencial del dipolo y la fuerza que actúa sobre él. | ||
| + | # Obtenga los momentos monopolar y dipolar del sistema de dos anillos y proporcione expresiones aproximadas para el potencial eléctrico y el campo eléctrico en puntos alejados del sistema | ||
| + | |||
| + | =={{nivel|1}} [[Campo debido a dos planos paralelos]]== | ||
| + | [[Imagen:2planoscargados01.gif|right]]Un condensador de placas planas puede aproximarse por dos dos planos paralelos, separados una distancia <math>a</math>. Uno de ellos, situado en <math>z=-a/2</math> posee una distribución de carga uniforme <math>\sigma_0</math>, mientras que la del otro, situado en <math>z=a/2</math> es <math>-\sigma_0</math>. Halle el campo eléctrico en todos los puntos del espacio. | ||
| + | |||
| + | =={{nivel|4}} [[Campo debido a una superficie esférica cargada]]== | ||
| + | Una esfera de radio <math>R</math> almacena una carga <math>Q</math> distribuida uniformemente en su superficie. Calcule el campo eléctrico producido por la esfera en todos los puntos del espacio | ||
| + | |||
| + | # Aplicando las leyes de la electrostática | ||
| + | # Por integración directa | ||
| + | |||
| + | =={{nivel|3}} [[Campo de una distribución cilíndrica]]== | ||
| + | [[Imagen:cilindroscargados.png|right]]Un cilindro de radio <math>a</math> y longitud indefinida, mucho mayor que el radio, está relleno de sendas distribuciones de carga eléctrica de signo opuesto y densidades volumétricas constantes <math>\rho_0</math> y <math>-\rho_0</math>, según se muestra en la figura. Además, en la superficie de separación entre ambas distribuciones, <math>\rho=a/2</math>, existe una distribución superficial uniforme de carga. | ||
| + | |||
| + | # Calcule el valor de dicha densidad superficial de carga si el campo eléctrico es nulo en los puntos exteriores al cilindro | ||
| + | # Obtenga la expresión del campo eléctrico en todo el espacio | ||
| + | # Calcule la diferencia de potencial entre el centro de la distribución y la superficie exterior. | ||
| + | # Halle la densidad de energía electrostática en cualquier punto del espacio, así como la energía almacenada entre dos planos <math>z=0</math> y <math>z=h</math>. | ||
| + | |||
| + | =={{nivel|2}} [[Campo debido a una esfera cargada uniformemente]]== | ||
Una esfera de radio <math>R</math> almacena una carga <math>Q</math> distribuida uniformemente en su volumen. | Una esfera de radio <math>R</math> almacena una carga <math>Q</math> distribuida uniformemente en su volumen. | ||
# Calcule el campo eléctrico producido por la esfera en todos los puntos del espacio. | # Calcule el campo eléctrico producido por la esfera en todos los puntos del espacio. | ||
| - | # Halle la fuerza que experimenta un dipolo \mathbf{p} situado en el interior de esta nube de carga. | + | # Halle la fuerza que experimenta un dipolo <math>\mathbf{p}</math> situado en el interior de esta nube de carga. |
| + | |||
| + | =={{nivel|3}} [[Modelo de molécula de hidrógeno]]== | ||
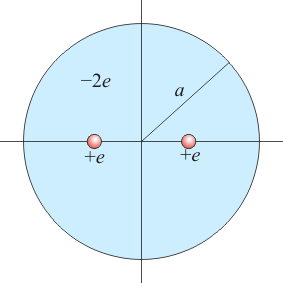
| + | [[Archivo:molecula-hidrogeno.png|right]] | ||
| + | |||
| + | Un modelo simple de la molécula de hidrógeno es el siguiente: tenemos dos cargas puntuales (los núcleos) de valor <math>+e</math> inmersas en una nube esférica de radio <math>a</math>, con carga <math>-2e</math> distribuida uniformemente. | ||
| + | |||
| + | # Determine la posición de equilibrio entre las dos cargas puntuales, suponiendo que se encuentran situadas simétricamente respecto al centro de la nube. | ||
| + | # Calcule el potencial y el campo eléctrico en todos los puntos del espacio en la situación anterior. | ||
| + | # Suponga que las dos cargas positivas se desplazan una cantidad <math>c=a/4</math> a lo largo de la recta que las une, manteniendo la distancia entre ellas. En este caso, ¿qué campo se ve en el exterior de la molécula? ¿cuáles son los dos primeros momentos del desarrollo multipolar del potencial eléctrico? | ||
| + | # Calcule el trabajo necesario para realizar el desplazamiento del apartado anterior. | ||
| - | == | + | =={{nivel|3}} [[Una esfera conductora rellena de una densidad de carga|Una esfera conductora rellena]]== |
[[Imagen:esferarhor.gif|right]]Una superficie esférica conductora de radio <math>R</math>, puesta a tierra, contiene en su interior una distribución de carga no uniforme, cuya densidad de carga es de la forma | [[Imagen:esferarhor.gif|right]]Una superficie esférica conductora de radio <math>R</math>, puesta a tierra, contiene en su interior una distribución de carga no uniforme, cuya densidad de carga es de la forma | ||
| Línea 80: | Línea 126: | ||
# Halle la energía electrostática almacenada en el sistema. | # Halle la energía electrostática almacenada en el sistema. | ||
| - | ===[[Flujo del campo eléctrico de una carga]] | + | =={{nivel|3}} [[Cilindro relleno de una densidad de carga no uniforme]]== |
| + | El interior de un tubo cilínndrico de radio ''a'' y longitud indefinida está ocupado por un gas que presenta una distribución volumétrica de carga eléctrica, <math>\rho_q</math>, que varía con la distancia <math>\rho</math> al eje del tubo, según la ley | ||
| + | |||
| + | <center><math>\rho_q(\mathbf{r})=\rho_q(\rho)=k\left(1+\frac{2\rho^2}{a^2}\right)</math></center> | ||
| + | |||
| + | Inicialmente, no hay más cargas en el sistema. | ||
| + | |||
| + | # Determine la cantidad de carga contenida en una porción del tubo de longitud <math>h</math>, así como la expresión del campo eléctrico en todos los puntos del espacio. | ||
| + | # ¿Qué distribución superficial de carga debe añadirse en la superficie del tubo para que el campo eléctrico exterior sea nulo? Para ese caso, determine el potencial electrostático en todos los puntos del espacio. | ||
| + | # Supóngase que en el punto <math>\mathbf{r}= b\mathbf{u}_x\;\; (b < a)</math> se encuentra una molécula de agua con momento dipolar <math>\mathbf{p}_0 = p\mathbf{u}_x</math>. ¿Cómo es la fuerza que el gas ejerce sobre ella? ¿A qué se reduce la fuerza si b = 0? | ||
| + | |||
| + | =={{nivel|2}} [[Flujo del campo eléctrico de una carga]]== | ||
Halle el flujo del campo eléctrico debido a una carga puntual <math>q</math> a través de un disco cuyo eje pasa por el punto donde se encuentra la carga. | Halle el flujo del campo eléctrico debido a una carga puntual <math>q</math> a través de un disco cuyo eje pasa por el punto donde se encuentra la carga. | ||
| Línea 88: | Línea 145: | ||
# Usando coordenadas esféricas (''Sugerencia'': En lugar del disco emplee otra superficie que abarque el mismo ángulo sólido). | # Usando coordenadas esféricas (''Sugerencia'': En lugar del disco emplee otra superficie que abarque el mismo ángulo sólido). | ||
| - | == | + | =={{nivel|2}} [[Campo eléctrico de una esfera horadada]]== |
| - | En un volumen en forma de esfera (de radio <math>3R</math>) en la que se han hecho dos huecos (también esféricos, uno de radio <math>2R</math> y otro de radio <math>R</math>) se distribuye uniformemente una carga <math>Q</math>. | + | [[Imagen:esferadoshuecos.png|left]]En un volumen en forma de esfera (de radio <math>3R</math>) en la que se han hecho dos huecos (también esféricos, uno de radio <math>2R</math> y otro de radio <math>R</math>) se distribuye uniformemente una carga <math>Q</math>. |
# Calcule el campo eléctrico en el punto <math>P</math>, de tangencia de los dos huecos. | # Calcule el campo eléctrico en el punto <math>P</math>, de tangencia de los dos huecos. | ||
| Línea 95: | Línea 152: | ||
# Calcule los dos primeros momentos multipolares del sistema, tomando como origen de coordenadas el centro de la esfera grande. | # Calcule los dos primeros momentos multipolares del sistema, tomando como origen de coordenadas el centro de la esfera grande. | ||
| - | == | + | =={{nivel|3}} [[Campo de un anillo no uniforme]]== |
| - | En el plano <math>XY</math> se encuentra una distribución de carga lineal, formando un anillo, de radio <math>R</math> y con una distribución de carga no | + | [[Imagen:anillonouniforme.gif|right]]En el plano <math>XY</math> se encuentra una distribución de carga lineal, formando un anillo, de radio <math>R</math> y con una distribución de carga no uniforme dada, en coordenadas cilíndricas, por |
| - | uniforme dada, en coordenadas cilíndricas, por | + | |
<center><math>\lambda=\lambda_0\cos\varphi'</math>{{qquad}}<math>\varphi'\in(-\pi,\pi]</math></center> | <center><math>\lambda=\lambda_0\cos\varphi'</math>{{qquad}}<math>\varphi'\in(-\pi,\pi]</math></center> | ||
| Línea 105: | Línea 161: | ||
# Demuestre que, para puntos alejados, su campo se comporta como el de un dipolo, ¿cuál sería el valor y la orientación de dicho dipolo? | # Demuestre que, para puntos alejados, su campo se comporta como el de un dipolo, ¿cuál sería el valor y la orientación de dicho dipolo? | ||
| - | == | + | =={{nivel|1}} [[Potencial de dos cargas puntuales]]== |
Halle el potencial creado por dos cargas <math>q_1</math>, <math>-q_2</math> situadas a una distancia <math>a</math> una de la otra. Demuestre que la superficie equipotencial <math>V=0</math> es una esfera. | Halle el potencial creado por dos cargas <math>q_1</math>, <math>-q_2</math> situadas a una distancia <math>a</math> una de la otra. Demuestre que la superficie equipotencial <math>V=0</math> es una esfera. | ||
| - | == | + | =={{nivel|1}} [[Flujo del campo eléctrico a través de una superficie abierta]]== |
Se tienen dos cargas puntuales de valor <math>q</math> situadas en los puntos <math>\pm(a/2)\mathbf{u}_{y}</math>. Halle el flujo del campo eléctrico a través de un triángulo con vértices en los puntos <math>a\mathbf{u}_{x}</math>, <math>a\mathbf{u}_{y}</math> y <math>a\mathbf{u}_{z}</math>. | Se tienen dos cargas puntuales de valor <math>q</math> situadas en los puntos <math>\pm(a/2)\mathbf{u}_{y}</math>. Halle el flujo del campo eléctrico a través de un triángulo con vértices en los puntos <math>a\mathbf{u}_{x}</math>, <math>a\mathbf{u}_{y}</math> y <math>a\mathbf{u}_{z}</math>. | ||
| - | ===[[Diferencia de potencial entre dos discos]] | + | =={{nivel|4}} [[Potencial eléctrico de un segmento cargado]]== |
| + | Sea un segmento rectilíneo de longitud <math>L</math>, sobre el cual existe una densidad de carga uniforme <math>\lambda</math>. | ||
| + | |||
| + | # Halle el potencial que produce en un punto cualquiera del espacio. | ||
| + | # Demuestre que las equipotenciales son elipsoides con focos los extremos del segmento. | ||
| + | |||
| + | =={{nivel|3}} [[Diferencia de potencial entre dos discos]]== | ||
Se tienen dos discos plásticos de radio 1 cm y espesor despreciable, sobre los cuales se distribuyen de manera uniforme cargas de +1 nC y −1nC respectivamente. Estos discos se disponen paralelamente a una distancia <math>a</math>. Determine | Se tienen dos discos plásticos de radio 1 cm y espesor despreciable, sobre los cuales se distribuyen de manera uniforme cargas de +1 nC y −1nC respectivamente. Estos discos se disponen paralelamente a una distancia <math>a</math>. Determine | ||
| Línea 118: | Línea 180: | ||
# Determine exactamente la diferencia de potencial entre los centros para cualquier valor de <math>a</math>. Compare el resultado con los dos anteriores. ¿Cuánto es aproximadamente el error cometido en el primer apartado? ¿Y en el segundo? | # Determine exactamente la diferencia de potencial entre los centros para cualquier valor de <math>a</math>. Compare el resultado con los dos anteriores. ¿Cuánto es aproximadamente el error cometido en el primer apartado? ¿Y en el segundo? | ||
| - | == | + | =={{nivel|2}} [[Potencial en el centro de una esfera]]== |
Calcule el potencial eléctrico en el centro de una esfera de radio <math>R</math>, cargada con una carga <math>Q_0</math> distribuida… | Calcule el potencial eléctrico en el centro de una esfera de radio <math>R</math>, cargada con una carga <math>Q_0</math> distribuida… | ||
| Línea 126: | Línea 188: | ||
# en su volumen con una densidad <math>\rho = A r</math> (calcule previamente el valor de la constante <math>A</math>). | # en su volumen con una densidad <math>\rho = A r</math> (calcule previamente el valor de la constante <math>A</math>). | ||
| - | == | + | =={{nivel|2}} [[Potencial de una línea de carga]]== |
| - | Determine el potencial eléctrico creado en todos los puntos del espacio por una línea recta infinita, cargada con una densidad uniforme <math>\lambda_0</math>, estando el origen de potencial situado a una distancia | + | Determine el potencial eléctrico creado en todos los puntos del espacio por una línea recta infinita, cargada con una densidad uniforme <math>\lambda_0</math>, estando el origen de potencial situado a una distancia <math>a</math> de la línea. ¿Por qué no puede tomarse el infinito como origen de potencial? |
| - | A partir de este resultado, calcule el potencial creado por dos líneas infinitas de carga, con densidades uniformes <math>+\lambda_0</math> y <math>-\lambda_0</math>, situadas paralelamente a una distancia | + | A partir de este resultado, calcule el potencial creado por dos líneas infinitas de carga, con densidades uniformes <math>+\lambda_0</math> y <math>-\lambda_0</math>, situadas paralelamente a una distancia <math>2a</math>, tomando como origen de potencial un punto equidistante de ambas líneas. |
| - | == | + | =={{nivel|1}} [[Energía de tres cargas en un triángulo]]== |
Calcule la energía electrostática almacenada en cada una de las cuatro configuraciones del problema de [[tres cargas en un triángulo equilátero]]. | Calcule la energía electrostática almacenada en cada una de las cuatro configuraciones del problema de [[tres cargas en un triángulo equilátero]]. | ||
| - | == | + | =={{nivel|1}} [[Trabajo para reunir cuatro cargas]]== |
Para la configuración del problema de [[cuatro cargas en un rectángulo]], calcule el trabajo necesario para llevar la carga <math>q_4</math> desde el infinito hasta su posición final. | Para la configuración del problema de [[cuatro cargas en un rectángulo]], calcule el trabajo necesario para llevar la carga <math>q_4</math> desde el infinito hasta su posición final. | ||
| - | == | + | =={{nivel|1}} [[Trabajo para cuatro cargas en un cuadrado]]== |
Cuatro cargas puntuales se sitúan en los vértices de un cuadrado de lado <math>a</math>. Dos de ellas, situadas en vértices adyacentes, son de valor <math>+q</math>, mientras que las otras dos valen <math>-q</math>. | Cuatro cargas puntuales se sitúan en los vértices de un cuadrado de lado <math>a</math>. Dos de ellas, situadas en vértices adyacentes, son de valor <math>+q</math>, mientras que las otras dos valen <math>-q</math>. | ||
| Línea 146: | Línea 208: | ||
Si la carga positiva se permuta con la negativa situada en el vértice vecino, ¿cuál será en este caso, el trabajo realizado? | Si la carga positiva se permuta con la negativa situada en el vértice vecino, ¿cuál será en este caso, el trabajo realizado? | ||
| - | == | + | =={{nivel|3}} [[Carga, potencial y energía de un campo dado]]== |
| - | En el espacio vacío se ha detectado un campo electrostático con simetría esférica respecto de un punto fijo <math>O</math>, cuya función de campo | + | En el espacio vacío se ha detectado un campo electrostático con simetría esférica respecto de un punto fijo <math>O</math>, cuya función de campo viene dada por la expresión <math>\mathbf{E}(\mathbf{r})=E(r)\mathbf{u}_{r}</math>, con |
| - | viene dada por la expresión <math>\mathbf{E}(\mathbf{r})=E(r)\mathbf{u}_{r}</math>, con | + | |
<center><math>E(r) = \begin{cases}E_0\displaystyle\frac{r}{a} & 0\leq r<a \\ & \\ E_0 & a< r < b \\ & \\ E_0\left(\displaystyle\frac{a}{r}\right)^2 & b<r \end{cases}</math></center> | <center><math>E(r) = \begin{cases}E_0\displaystyle\frac{r}{a} & 0\leq r<a \\ & \\ E_0 & a< r < b \\ & \\ E_0\left(\displaystyle\frac{a}{r}\right)^2 & b<r \end{cases}</math></center> | ||
| Línea 159: | Línea 220: | ||
# ¿Cuánto vale la energía electrostática del sistema? | # ¿Cuánto vale la energía electrostática del sistema? | ||
| - | ===[[Campo y carga de un potencial conocido]] | + | =={{nivel|3}} [[Campo eléctrico con simetría cilíndrica]]== |
| + | Un campo eléctrico con simetría cilíndrica está definido por la siguiente expresión, expresada en coordenadas cilíndricas: | ||
| + | |||
| + | <center><math>\mathbf{E}(\rho,\varphi,z)=\begin{cases} | ||
| + | \displaystyle E_0\left(\frac{\rho}{a}\right)^2\mathbf{u}_\rho & (0\leq\rho<a)\\ & \\ \displaystyle -E_0\mathbf{u}_\rho\, & | ||
| + | (a<\rho< b) \\ & \\ \mathbf{0} & (b<\rho)\end{cases}</math></center> | ||
| + | |||
| + | # Determine las distribuciones de carga que producen este campo eléctrico, así como la carga eléctrica total. | ||
| + | # Obtenga la expresión del potencial electrostático creado por esas distribuciones. | ||
| + | # Halle la energía electrostática almacenada entre dos planos <math>z=0</math> y <math>z=h</math>. | ||
| + | |||
| + | =={{nivel|2}} [[Campo y carga de un potencial conocido]]== | ||
El potencial eléctrico en todos los puntos del espacio viene dado por la ecuación | El potencial eléctrico en todos los puntos del espacio viene dado por la ecuación | ||
| Línea 169: | Línea 241: | ||
# Calcule la densidad de carga que crea este campo eléctrico. | # Calcule la densidad de carga que crea este campo eléctrico. | ||
| - | ===[[Energía de una esfera cargada]] | + | =={{nivel|3}} [[Modelo de campo atómico]]== |
| + | El potencial medio temporal de un átomo de hidrógeno neutro viene dado | ||
| + | por | ||
| + | |||
| + | <center><math>\phi = \frac{q \mathrm{e}^{-\alpha r}}{4\pi\varepsilon_0 r} \left( 1 + \frac{\alpha | ||
| + | r}{2} \right)</math></center> | ||
| + | |||
| + | en donde <math>q</math> es la carga electrónica, y <math>\alpha^{-1}=a_0 / 2</math>. Halle la distribución de carga (continua y discreta) que dará lugar a este potencial e interprete este resultado físicamente. | ||
| + | |||
| + | =={{nivel|2}} [[Energía de esferas concéntricas]]== | ||
| + | [[Imagen:dosesferasconcentricas.png|left]]Halle la energía electrostática almacenada en una superficie esférica de radio <math>a</math>, que almacena una carga <math>Q</math>, distribuida uniformemente sobre ella. | ||
| + | |||
| + | Calcule la energía electrostática almacenada en un sistema de dos superficies esféricas concéntricas de radios <math>a</math> y <math>b</math>, cargadas, respectivamente con cargas <math>+Q</math> y <math>-Q</math>, distribuidas uniformemente. | ||
| + | |||
| + | ¿Se verifica el principio de superposición, esto es, es la energía de las dos esferas la suma de las energías de cada esfera por separado? | ||
| + | |||
| + | =={{nivel|2}} [[Energía de una esfera cargada]]== | ||
Calcule la energía libre electrostática de: | Calcule la energía libre electrostática de: | ||
| Línea 177: | Línea 265: | ||
# El llamado ''radio clásico del electrón'' se obtiene describiendo esta partícula como una pequeña esfera de radio <math>a</math>, cargada uniformemente en su superficie. Suponiendo que la energía electrostática almacenada en el sistema equivale a la masa del electrón de acuerdo con la ley <math>E=mc^2</math>, halle el valor ''numérico'' del radio que debería tener el electrón. Repita ahora el cálculo para el caso de un protón. ¿Es lógico el resultado que se obtiene? | # El llamado ''radio clásico del electrón'' se obtiene describiendo esta partícula como una pequeña esfera de radio <math>a</math>, cargada uniformemente en su superficie. Suponiendo que la energía electrostática almacenada en el sistema equivale a la masa del electrón de acuerdo con la ley <math>E=mc^2</math>, halle el valor ''numérico'' del radio que debería tener el electrón. Repita ahora el cálculo para el caso de un protón. ¿Es lógico el resultado que se obtiene? | ||
| - | == | + | =={{nivel|3}} [[Fuerza entre un anillo y un dipolo]]== |
| - | Un anillo circular de radio <math>a</math>, almacena una carga | + | Un anillo circular de radio <math>a</math>, almacena una carga <math>Q</math> distribuida uniformemente. En el centro del anillo se encuentra un dipolo puntual <math>\mathbf{p}</math>, alineado según el eje de la espira. |
# Determine la fuerza que el dipolo ejerce sobre la espira. | # Determine la fuerza que el dipolo ejerce sobre la espira. | ||
| Línea 185: | Línea 273: | ||
# Calcule el par que la espira ejerce sobre el dipolo. | # Calcule el par que la espira ejerce sobre el dipolo. | ||
| - | == | + | =={{nivel|3}} [[Interacción entre dos dipolos eléctricos]]== |
Se tiene un dipolo puntual <math>\mathbf{p}_1=p\mathbf{u}_{z}</math> sobre el cual situamos el origen de coordenadas. Se coloca un segundo dipolo de la misma magnitud, pero diferente orientación, en el punto <math>a\mathbf{u}_{z}</math>. | Se tiene un dipolo puntual <math>\mathbf{p}_1=p\mathbf{u}_{z}</math> sobre el cual situamos el origen de coordenadas. Se coloca un segundo dipolo de la misma magnitud, pero diferente orientación, en el punto <math>a\mathbf{u}_{z}</math>. | ||
| Línea 192: | Línea 280: | ||
# Repita el cálculo si <math>\mathbf{p}_2=p\mathbf{u}_{x}</math>. | # Repita el cálculo si <math>\mathbf{p}_2=p\mathbf{u}_{x}</math>. | ||
| - | == | + | =={{nivel|2}} [[Cálculo de momentos multipolares]]== |
Halle los momentos monopolar (carga) y dipolar de las siguientes distribuciones de cargas. Describa el campo y el potencial eléctrico a gran distancia de ellas: | Halle los momentos monopolar (carga) y dipolar de las siguientes distribuciones de cargas. Describa el campo y el potencial eléctrico a gran distancia de ellas: | ||
| Línea 203: | Línea 291: | ||
# Una esfera con densidad de carga <math>\rho=\rho_0\cos\theta</math>. | # Una esfera con densidad de carga <math>\rho=\rho_0\cos\theta</math>. | ||
| - | + | =={{nivel|3}} [[Potencial y campo en el centro de una semicorona esférica]]== | |
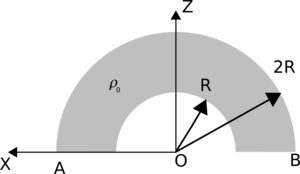
| - | + | [[Imagen:Semicorona.png|right|300px]]Se tiene el sistema de la figura, formado por una semicorona esférica de radios <math>R</math> y <math>2R</math>, con una densidad volumétrica de carga uniforme <math>\rho_0</math>. Se pide | |
| - | + | ||
| - | Se tiene el sistema de la figura, formado por una semicorona esférica de radios <math>R</math> y <math>2R</math>, con una densidad volumétrica de carga uniforme <math>\rho_0</math>. Se pide | + | |
# Calcular el potencial eléctrico en el punto O. | # Calcular el potencial eléctrico en el punto O. | ||
| Línea 212: | Línea 298: | ||
# Calcular el campo eléctrico en el punto O. | # Calcular el campo eléctrico en el punto O. | ||
# Calcular, hasta el segundo orden de aproximación, la expresión aproximada del potencial en puntos alejados del sistema. | # Calcular, hasta el segundo orden de aproximación, la expresión aproximada del potencial en puntos alejados del sistema. | ||
| + | |||
| + | =={{nivel|2}} [[Sistema electrostático de tres cargas puntuales]]== | ||
| + | [[Archivo:P1_sept_11_12_ceit_0.gif|right]]Un sistema electrostático está formado por tres cargas eléctricas puntuales. Dos de ellas tienen idéntico valor <math>q=3\,\mathrm{nC}</math> y se hallan en los puntos <math>P_1</math> y <math>P_2</math>, dados por los vectores de posición <math>\mathbf{r}_1=+12\mathbf{u}_x\,\mathrm{(cm)}</math> y <math>\mathbf{r}_2=-12\mathbf{u}_x\,\mathrm{(cm)}</math>, respectivamente. La tercera carga tiene un valor <math>Q</math> y se halla en el punto <math>P_3</math>, dado por <math>\mathbf{r}_3=-16\mathbf{u}_y\,\mathrm{(cm)}</math>. | ||
| + | |||
| + | # Determine, si es posible, el valor que debe tener la carga <math>Q</math> y la posición <math>\mathbf{r}_0=y_0\mathbf{u}_y</math> de un punto del eje <math>OY</math> en el cuál se anulen simultáneamente el potencial y el campo eléctrico creado por el sistema de tres cargas. | ||
| + | # ¿Cuál es la energía electrostática del sistema descrito en el caso particular <math>Q=-10 \,\mathrm{nC}</math>? | ||
| + | # En la situación particular del apartado anterior, ¿qué trabajo hay que realizar para traer una carga <math>q</math> desde el infinito hasta el punto de posición <math>\mathbf{r}_4=+9\mathbf{u}_y\,\mathrm{(cm)}</math>. ¿Cuánto vale la fuerza electrostática ejercida sobre dicha carga este punto? | ||
| + | # Determine los momentos monopolar y dipolar de la distribución correspondiente al apartado 2. Halle el potencial exacto y el aproximado por el desarrollo multipolar, para el punto <math>\mathbf{r}_5=+36\mathbf{u}_x\,\mathrm{(cm)}</math>. Calcule el error relativo cometido en la aproximación, según la fórmula | ||
| + | |||
| + | <center><math>\epsilon=\left|\frac{V_\mathrm{aprox}-V_\mathrm{exac}}{V_\mathrm{exac}}\right|</math></center> | ||
| - | |||
| - | + | [[Categoría:Problemas de electrostática en el vacío|0]] | |
| - | + | [[Categoría:Problemas de Campos Electromagnéticos|20]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | 0 | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
última version al 13:02 18 sep 2012
1  Modelo semiclásico del átomo de Bohr
Modelo semiclásico del átomo de Bohr
Supongamos un protón y un electrón situados a una distancia de un radio de Bohr
- Calcule la fuerza eléctrica entre las dos partículas.
- Halle la fuerza gravitatoria entre ellas.
- Calcule el cociente entre las fuerza eléctrica y la gravitatoria.
- Suponga que en lugar a una distancia de un radio de Bohr el protón se encuentra en el centro de la Tierra y el electrón en el centro de la Luna (a 384000 km), ¿cómo cambian las fuerzas eléctrica y gravitatoria? ¿Y el cociente entre ellas? De acuerdo con este resultado, ¿cómo se explica que la fuerza dominante en el sistema Tierra-Luna sea la gravedad?
2  Electroscopio de dos hilos
Electroscopio de dos hilos
Un electroscopio mide la carga por la desviación angular de dos esferas idénticas conductoras, suspendidas por cuerdas aislantes de masas despreciables y longitud l. Cada esfera tiene una masa m y está sometida a la gravedad 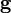 . Las cargas pueden considerarse como puntuales e iguales entre sí. Halle la ecuación que liga el semiángulo θ con el valor de la carga total Q depositada en las esferas.
. Las cargas pueden considerarse como puntuales e iguales entre sí. Halle la ecuación que liga el semiángulo θ con el valor de la carga total Q depositada en las esferas.
Suponga que la masa de cada esfera es 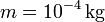 y la
longitud del cable del que penden es 20 cm. Admita asimismo que los ángulos de desviación pueden medirse como mucho con una precisión de 1°. ¿Cuál es la carga mínima que puede medirse con este aparato? ¿Y la carga máxima?
y la
longitud del cable del que penden es 20 cm. Admita asimismo que los ángulos de desviación pueden medirse como mucho con una precisión de 1°. ¿Cuál es la carga mínima que puede medirse con este aparato? ¿Y la carga máxima?
3  Tres cargas en un triángulo equilátero
Tres cargas en un triángulo equilátero
Tres cargas q1, q2 y q3, se encuentran en los vértices de un triángulo equilátero de lado a = 1cm. Determine la fuerza sobre cada carga cuando:
-
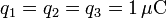 .
.
-
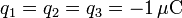 .
.
-
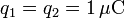 ,
, 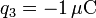 .
.
-
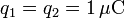 ,
, 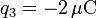 .
.
4  Cuatro cargas en un rectángulo
Cuatro cargas en un rectángulo
Una carga puntual 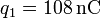 se encuentra situada en el
origen de coordenadas. En
se encuentra situada en el
origen de coordenadas. En 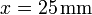 ,
, 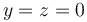 se halla una segunda carga q2. En
se halla una segunda carga q2. En 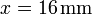 ,
, 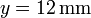 se encuentra una tercera carga q3.
se encuentra una tercera carga q3.
Calcule el valor que deben tener q2 y q3 si, ocupando las´posiciones indicadas, se desea que sea nula la fuerza sobre una carga 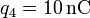 situada en
situada en 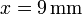 ,
, 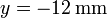 , z = 0.
, z = 0.
5  Tres cargas en un anillo
Tres cargas en un anillo
Se dispone de tres cargas, una de valor Q y las otras dos de valor q. Estas cargas se ensartan en un anillo circular de radio R sobre el cual pueden deslizar libremente. Determine la ecuación para los ángulos del triángulo que forman las tres cargas. ¿Cuál es la solución para los casos 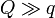 ,
, 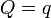 y
y 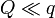 ?
?
6  Fuerza entre dos varillas colineales
Fuerza entre dos varillas colineales
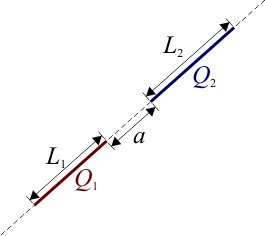
Calcule la fuerza entre dos varillas colineales, de longitudes L1 y L2, que almacenan respectivamente cargas Q1 y Q2, cuando sus extremos más próximos distan una cantidad a.
7  Campo eléctrico de un segmento cargado
Campo eléctrico de un segmento cargado
Sea un segmento rectilíneo de longitud L, sobre el cual existe una densidad de carga uniforme λ.
Halle el campo eléctrico que produce en un punto arbitrario del espacio
- ¿A qué se reduce el campo en el plano central del segmento?
- Calcule el límite del campo del segmento para
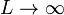 .
.
8  Fuerza entre dos hilos cargados
Fuerza entre dos hilos cargados
Un cable formado por dos hilos paralelos produce un campo eléctrico similar al producido por dos líneas infinitas con densidad de carga λ y − λ, situadas a una distancia D una de la otra.
Halle la fuerza que uno de los hilos produce sobre un segmento de longitud h del otro hilo.
9  Campo eléctrico entre dos varillas
Campo eléctrico entre dos varillas
Dos varillas rectilíneas de longitud L están situadas paralelamente a una distancia D. Las varillas poseen cargas 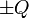 distribuidas uniformemente.
distribuidas uniformemente.
- Halle aproximadamente el campo eléctrico en un punto P equidistante de ambas varillas, para el caso
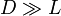 .
.
- Calcule, también de forma aproximada, el valor del campo en el mismo punto P, para el caso
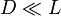 .
.
- Calcule el valor exacto del campo eléctrico en dicho punto P, para un valor arbitrario de D.
- Compare los valores exactos y aproximados para el caso
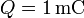 ,
, 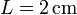 , y
, y
-
10  Una varilla y una carga
Una varilla y una carga
Una carga eléctrica Q está uniformemente distribuida a lo largo de un segmento rectilíneo de longitud 2a. A una distancia a del punto medio de dicho segmento y en dirección perpendicular a éste, se halla una carga puntual − Q.
- Calcule el flujo del campo eléctrico a través de una superficie esférica de radio a / 2 centrada en el punto medio del segmento cargado (punto O).
- Obtenga la fuerza que actúa sobre la carga puntual.
- Calcule los momentos monopolar y dipolar de la distribución de carga descrita. Proponga expresiones aproximadas para el potencial y el campo eléctrico en puntos suficientemente alejados de la distribución.
- ¿Qué trabajo habría que realizar para mover la carga puntual entre los puntos A al B? (ver figura)
11  Campo en el eje de un anillo
Campo en el eje de un anillo
Halle el campo eléctrico en todos los puntos del eje de un anillo de radio R sobre el cual hay una densidad de carga uniforme λ.
A partir de este resultado, calcule el campo creado por una corona circular de radios R1 y R2 (R1 < R2), sobre la cual hay una densidad de carga uniforme σ0, en los puntos de su eje.
¿A que se reduce si 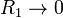 ? ¿Y si
? ¿Y si 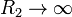 ? Considere en particular el comportamiento en las proximidades de z = 0.
? Considere en particular el comportamiento en las proximidades de z = 0.
12  Campo de dos anillos coaxiales
Campo de dos anillos coaxiales
Dos anillos iguales de radio R y grosor despreciable están cargados eléctricamente con sendas distribuciones lineales y uniformes + λ0 y − λ0. Los anillos se encuentran en planos paralelos separados una distancia R, pero con sus centros situados sobre el mismo eje. Tómese este eje como Z, y como origen de coordenadas O el punto medio entre los anillos.
- Obtenga la expresión del potencial electrostático creado por estas distribuciones en los puntos del eje Z. Calcule el valor del potencial en un punto arbitrario del plano XY.
- Obtenga la expresión del campo eléctrico para los puntos del eje Z. ¿Cuánto vale la fuerza que actúa sobre una carga puntual q situada en O? ¿Qué trabajo se ha realizado para traer esta carga desde el infinito hasta este punto?
- Suponga que, en lugar de la carga puntual, se sitúa un dipolo eléctrico de momento dipolar
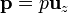 , en el centro del anillo de carga positiva. Obtenga la expresión de la energía potencial del dipolo y la fuerza que actúa sobre él.
, en el centro del anillo de carga positiva. Obtenga la expresión de la energía potencial del dipolo y la fuerza que actúa sobre él.
- Obtenga los momentos monopolar y dipolar del sistema de dos anillos y proporcione expresiones aproximadas para el potencial eléctrico y el campo eléctrico en puntos alejados del sistema
13  Campo debido a dos planos paralelos
Campo debido a dos planos paralelos
Un condensador de placas planas puede aproximarse por dos dos planos paralelos, separados una distancia a. Uno de ellos, situado en z = − a / 2 posee una distribución de carga uniforme σ0, mientras que la del otro, situado en z = a / 2 es − σ0. Halle el campo eléctrico en todos los puntos del espacio.
14  Campo debido a una superficie esférica cargada
Campo debido a una superficie esférica cargada
Una esfera de radio R almacena una carga Q distribuida uniformemente en su superficie. Calcule el campo eléctrico producido por la esfera en todos los puntos del espacio
- Aplicando las leyes de la electrostática
- Por integración directa
15  Campo de una distribución cilíndrica
Campo de una distribución cilíndrica
Un cilindro de radio a y longitud indefinida, mucho mayor que el radio, está relleno de sendas distribuciones de carga eléctrica de signo opuesto y densidades volumétricas constantes ρ0 y − ρ0, según se muestra en la figura. Además, en la superficie de separación entre ambas distribuciones, ρ = a / 2, existe una distribución superficial uniforme de carga.
- Calcule el valor de dicha densidad superficial de carga si el campo eléctrico es nulo en los puntos exteriores al cilindro
- Obtenga la expresión del campo eléctrico en todo el espacio
- Calcule la diferencia de potencial entre el centro de la distribución y la superficie exterior.
- Halle la densidad de energía electrostática en cualquier punto del espacio, así como la energía almacenada entre dos planos z = 0 y z = h.
16  Campo debido a una esfera cargada uniformemente
Campo debido a una esfera cargada uniformemente
Una esfera de radio R almacena una carga Q distribuida uniformemente en su volumen.
- Calcule el campo eléctrico producido por la esfera en todos los puntos del espacio.
- Halle la fuerza que experimenta un dipolo
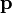 situado en el interior de esta nube de carga.
situado en el interior de esta nube de carga.
17  Modelo de molécula de hidrógeno
Modelo de molécula de hidrógeno
Un modelo simple de la molécula de hidrógeno es el siguiente: tenemos dos cargas puntuales (los núcleos) de valor + e inmersas en una nube esférica de radio a, con carga − 2e distribuida uniformemente.
- Determine la posición de equilibrio entre las dos cargas puntuales, suponiendo que se encuentran situadas simétricamente respecto al centro de la nube.
- Calcule el potencial y el campo eléctrico en todos los puntos del espacio en la situación anterior.
- Suponga que las dos cargas positivas se desplazan una cantidad c = a / 4 a lo largo de la recta que las une, manteniendo la distancia entre ellas. En este caso, ¿qué campo se ve en el exterior de la molécula? ¿cuáles son los dos primeros momentos del desarrollo multipolar del potencial eléctrico?
- Calcule el trabajo necesario para realizar el desplazamiento del apartado anterior.
18  Una esfera conductora rellena
Una esfera conductora rellena
Una superficie esférica conductora de radio R, puesta a tierra, contiene en su interior una distribución de carga no uniforme, cuya densidad de carga es de la forma
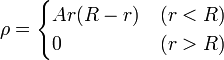
- Calcule el campo eléctrico en todos los puntos del espacio.
- Calcule el valor de la carga almacenada en la esfera conductora.
- Halle el potencial eléctrico en el centro de la esfera.
- A partir del campo eléctrico.
- Por integración directa a partir de las densidades de carga.
- Halle la energía electrostática almacenada en el sistema.
19  Cilindro relleno de una densidad de carga no uniforme
Cilindro relleno de una densidad de carga no uniforme
El interior de un tubo cilínndrico de radio a y longitud indefinida está ocupado por un gas que presenta una distribución volumétrica de carga eléctrica, ρq, que varía con la distancia ρ al eje del tubo, según la ley
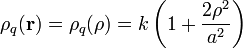
Inicialmente, no hay más cargas en el sistema.
- Determine la cantidad de carga contenida en una porción del tubo de longitud h, así como la expresión del campo eléctrico en todos los puntos del espacio.
- ¿Qué distribución superficial de carga debe añadirse en la superficie del tubo para que el campo eléctrico exterior sea nulo? Para ese caso, determine el potencial electrostático en todos los puntos del espacio.
- Supóngase que en el punto
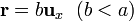 se encuentra una molécula de agua con momento dipolar
se encuentra una molécula de agua con momento dipolar 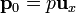 . ¿Cómo es la fuerza que el gas ejerce sobre ella? ¿A qué se reduce la fuerza si b = 0?
. ¿Cómo es la fuerza que el gas ejerce sobre ella? ¿A qué se reduce la fuerza si b = 0?
20  Flujo del campo eléctrico de una carga
Flujo del campo eléctrico de una carga
Halle el flujo del campo eléctrico debido a una carga puntual q a través de un disco cuyo eje pasa por el punto donde se encuentra la carga.
El disco tiene radio R y la distancia de la carga al plano del disco es h.
- Utilizando coordenadas cilíndricas
- Usando coordenadas esféricas (Sugerencia: En lugar del disco emplee otra superficie que abarque el mismo ángulo sólido).
21  Campo eléctrico de una esfera horadada
Campo eléctrico de una esfera horadada
En un volumen en forma de esfera (de radio 3R) en la que se han hecho dos huecos (también esféricos, uno de radio 2R y otro de radio R) se distribuye uniformemente una carga Q.
- Calcule el campo eléctrico en el punto P, de tangencia de los dos huecos.
- Halle el potencial eléctrico en el mismo punto P.
- Calcule los dos primeros momentos multipolares del sistema, tomando como origen de coordenadas el centro de la esfera grande.
22  Campo de un anillo no uniforme
Campo de un anillo no uniforme
En el plano XY se encuentra una distribución de carga lineal, formando un anillo, de radio R y con una distribución de carga no uniforme dada, en coordenadas cilíndricas, por
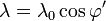
![\varphi'\in(-\pi,\pi]](/wiki/images/math/0/4/4/044ea3bbccb9a391ff5ff855c1f626b0.png)
- Halle el potencial eléctrico producido por el anillo en los puntos del eje Z.
- Calcule el campo eléctrico producido por el anillo en el mismo eje.
- Demuestre que, para puntos alejados, su campo se comporta como el de un dipolo, ¿cuál sería el valor y la orientación de dicho dipolo?
23  Potencial de dos cargas puntuales
Potencial de dos cargas puntuales
Halle el potencial creado por dos cargas q1, − q2 situadas a una distancia a una de la otra. Demuestre que la superficie equipotencial V = 0 es una esfera.
24  Flujo del campo eléctrico a través de una superficie abierta
Flujo del campo eléctrico a través de una superficie abierta
Se tienen dos cargas puntuales de valor q situadas en los puntos 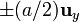 . Halle el flujo del campo eléctrico a través de un triángulo con vértices en los puntos
. Halle el flujo del campo eléctrico a través de un triángulo con vértices en los puntos 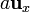 ,
, 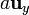 y
y 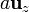 .
.
25  Potencial eléctrico de un segmento cargado
Potencial eléctrico de un segmento cargado
Sea un segmento rectilíneo de longitud L, sobre el cual existe una densidad de carga uniforme λ.
- Halle el potencial que produce en un punto cualquiera del espacio.
- Demuestre que las equipotenciales son elipsoides con focos los extremos del segmento.
26  Diferencia de potencial entre dos discos
Diferencia de potencial entre dos discos
Se tienen dos discos plásticos de radio 1 cm y espesor despreciable, sobre los cuales se distribuyen de manera uniforme cargas de +1 nC y −1nC respectivamente. Estos discos se disponen paralelamente a una distancia a. Determine
- El valor aproximado de la diferencia de potencial entre los centros cuando la distancia a = 1mm
- El valor aproximado del voltaje si a = 1 m.
- Determine exactamente la diferencia de potencial entre los centros para cualquier valor de a. Compare el resultado con los dos anteriores. ¿Cuánto es aproximadamente el error cometido en el primer apartado? ¿Y en el segundo?
27  Potencial en el centro de una esfera
Potencial en el centro de una esfera
Calcule el potencial eléctrico en el centro de una esfera de radio R, cargada con una carga Q0 distribuida…
- uniformemente en su superficie
- de forma no uniforme en su superficie, con densidad σs = σ0cosθ.
- uniformemente en su volumen
- en su volumen con una densidad ρ = Ar (calcule previamente el valor de la constante A).
28  Potencial de una línea de carga
Potencial de una línea de carga
Determine el potencial eléctrico creado en todos los puntos del espacio por una línea recta infinita, cargada con una densidad uniforme λ0, estando el origen de potencial situado a una distancia a de la línea. ¿Por qué no puede tomarse el infinito como origen de potencial?
A partir de este resultado, calcule el potencial creado por dos líneas infinitas de carga, con densidades uniformes + λ0 y − λ0, situadas paralelamente a una distancia 2a, tomando como origen de potencial un punto equidistante de ambas líneas.
29  Energía de tres cargas en un triángulo
Energía de tres cargas en un triángulo
Calcule la energía electrostática almacenada en cada una de las cuatro configuraciones del problema de tres cargas en un triángulo equilátero.
30  Trabajo para reunir cuatro cargas
Trabajo para reunir cuatro cargas
Para la configuración del problema de cuatro cargas en un rectángulo, calcule el trabajo necesario para llevar la carga q4 desde el infinito hasta su posición final.
31  Trabajo para cuatro cargas en un cuadrado
Trabajo para cuatro cargas en un cuadrado
Cuatro cargas puntuales se sitúan en los vértices de un cuadrado de lado a. Dos de ellas, situadas en vértices adyacentes, son de valor + q, mientras que las otras dos valen − q.
Calcule el trabajo para reunir esta distribución de cargas.
Suponga que una de las cargas positivas se intercambia con la negativa situada en el vértice opuesto, ¿qué trabajo hay que realizar para esta operación?
Si la carga positiva se permuta con la negativa situada en el vértice vecino, ¿cuál será en este caso, el trabajo realizado?
32  Carga, potencial y energía de un campo dado
Carga, potencial y energía de un campo dado
En el espacio vacío se ha detectado un campo electrostático con simetría esférica respecto de un punto fijo O, cuya función de campo viene dada por la expresión 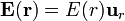 , con
, con
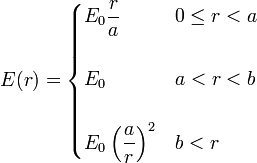
siendo r la distancia desde O al punto donde se evalúa el campo y E0, a y b$ son constantes conocidas.
- Determine cómo es la distribución de carga eléctrica que da lugar al campo descrito.
- Calcule la carga total de dicha distribución.
- Obtenga el valor del potencial eléctrico en O (
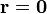 ).
).
- ¿Cuánto vale la energía electrostática del sistema?
33  Campo eléctrico con simetría cilíndrica
Campo eléctrico con simetría cilíndrica
Un campo eléctrico con simetría cilíndrica está definido por la siguiente expresión, expresada en coordenadas cilíndricas:
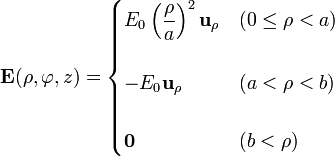
- Determine las distribuciones de carga que producen este campo eléctrico, así como la carga eléctrica total.
- Obtenga la expresión del potencial electrostático creado por esas distribuciones.
- Halle la energía electrostática almacenada entre dos planos z = 0 y z = h.
34  Campo y carga de un potencial conocido
Campo y carga de un potencial conocido
El potencial eléctrico en todos los puntos del espacio viene dado por la ecuación
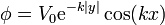
con k y V0 constantes.
- Halle el campo eléctrico en todos los puntos del espacio.
- Calcule la densidad de carga que crea este campo eléctrico.
35  Modelo de campo atómico
Modelo de campo atómico
El potencial medio temporal de un átomo de hidrógeno neutro viene dado por
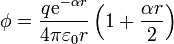
en donde q es la carga electrónica, y α − 1 = a0 / 2. Halle la distribución de carga (continua y discreta) que dará lugar a este potencial e interprete este resultado físicamente.
36  Energía de esferas concéntricas
Energía de esferas concéntricas
Halle la energía electrostática almacenada en una superficie esférica de radio a, que almacena una carga Q, distribuida uniformemente sobre ella.
Calcule la energía electrostática almacenada en un sistema de dos superficies esféricas concéntricas de radios a y b, cargadas, respectivamente con cargas + Q y − Q, distribuidas uniformemente.
¿Se verifica el principio de superposición, esto es, es la energía de las dos esferas la suma de las energías de cada esfera por separado?
37  Energía de una esfera cargada
Energía de una esfera cargada
Calcule la energía libre electrostática de:
- Una carga Q distribuida uniformemente sobre la superficie de una esfera de radio R.
- Una carga Q distribuida uniformemente en el volumen de una esfera de radio R.
- ¿Cuál de las dos configuraciones posee una menor energía almacenada? ¿Cómo se interpreta este resultado si se usa la integral de la densidad de energía
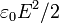 ?
?
- El llamado radio clásico del electrón se obtiene describiendo esta partícula como una pequeña esfera de radio a, cargada uniformemente en su superficie. Suponiendo que la energía electrostática almacenada en el sistema equivale a la masa del electrón de acuerdo con la ley E = mc2, halle el valor numérico del radio que debería tener el electrón. Repita ahora el cálculo para el caso de un protón. ¿Es lógico el resultado que se obtiene?
38  Fuerza entre un anillo y un dipolo
Fuerza entre un anillo y un dipolo
Un anillo circular de radio a, almacena una carga Q distribuida uniformemente. En el centro del anillo se encuentra un dipolo puntual 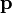 , alineado según el eje de la espira.
, alineado según el eje de la espira.
- Determine la fuerza que el dipolo ejerce sobre la espira.
- Halle la energía que tiene el dipolo por encontrarse en el campo de la espira.
- Calcule la fuerza que la espira produce sobre el dipolo. ¿Se verifica la tercera ley de Newton?
- Calcule el par que la espira ejerce sobre el dipolo.
39  Interacción entre dos dipolos eléctricos
Interacción entre dos dipolos eléctricos
Se tiene un dipolo puntual 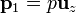 sobre el cual situamos el origen de coordenadas. Se coloca un segundo dipolo de la misma magnitud, pero diferente orientación, en el punto
sobre el cual situamos el origen de coordenadas. Se coloca un segundo dipolo de la misma magnitud, pero diferente orientación, en el punto 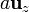 .
.
- Halle la fuerza y el par que el primer dipolo ejerce sobre el segundo si este está orientado como
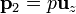 .
.
- Calcule el valor numérico de esta fuerza si los dos dipolos son moléculas de agua (
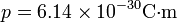 ) situadas a una distancia de
) situadas a una distancia de 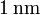 .
.
- Repita el cálculo si
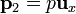 .
.
40  Cálculo de momentos multipolares
Cálculo de momentos multipolares
Halle los momentos monopolar (carga) y dipolar de las siguientes distribuciones de cargas. Describa el campo y el potencial eléctrico a gran distancia de ellas:
- Dos cargas de valor + q en los puntos
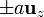
- Tres cargas positivas + q en los puntos
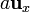 ,
, 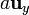 ,
, 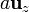 y tres negativas − q en
y tres negativas − q en 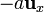 ,
, 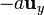 ,
, 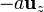 .
.
- Una varilla vertical de longitud L, centrada en el origen, con densidad de carga uniforme λ0.
- La misma varilla con una distribución de carga λ = kz.
- Una superficie esférica sobre la cual hay una distribución de carga σs = σ0cosθ.
- La misma superficie con distribuciones
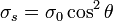 ,
, 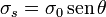 y
y 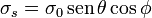
- Una esfera con densidad de carga ρ = ρ0cosθ.
41  Potencial y campo en el centro de una semicorona esférica
Potencial y campo en el centro de una semicorona esférica
Se tiene el sistema de la figura, formado por una semicorona esférica de radios R y 2R, con una densidad volumétrica de carga uniforme ρ0. Se pide
- Calcular el potencial eléctrico en el punto O.
- Calcular el trabajo necesario para trasladar una carga q desde el punto A hasta el punto B.
- Calcular el campo eléctrico en el punto O.
- Calcular, hasta el segundo orden de aproximación, la expresión aproximada del potencial en puntos alejados del sistema.
42  Sistema electrostático de tres cargas puntuales
Sistema electrostático de tres cargas puntuales
Un sistema electrostático está formado por tres cargas eléctricas puntuales. Dos de ellas tienen idéntico valor 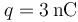 y se hallan en los puntos P1 y P2, dados por los vectores de posición
y se hallan en los puntos P1 y P2, dados por los vectores de posición 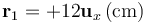 y
y 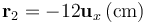 , respectivamente. La tercera carga tiene un valor Q y se halla en el punto P3, dado por
, respectivamente. La tercera carga tiene un valor Q y se halla en el punto P3, dado por 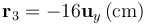 .
.
- Determine, si es posible, el valor que debe tener la carga Q y la posición
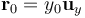 de un punto del eje OY en el cuál se anulen simultáneamente el potencial y el campo eléctrico creado por el sistema de tres cargas.
de un punto del eje OY en el cuál se anulen simultáneamente el potencial y el campo eléctrico creado por el sistema de tres cargas.
- ¿Cuál es la energía electrostática del sistema descrito en el caso particular
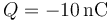 ?
?
- En la situación particular del apartado anterior, ¿qué trabajo hay que realizar para traer una carga q desde el infinito hasta el punto de posición
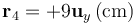 . ¿Cuánto vale la fuerza electrostática ejercida sobre dicha carga este punto?
. ¿Cuánto vale la fuerza electrostática ejercida sobre dicha carga este punto?
- Determine los momentos monopolar y dipolar de la distribución correspondiente al apartado 2. Halle el potencial exacto y el aproximado por el desarrollo multipolar, para el punto
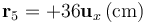 . Calcule el error relativo cometido en la aproximación, según la fórmula
. Calcule el error relativo cometido en la aproximación, según la fórmula