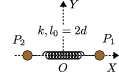De Laplace

Revisión a fecha de 09:06 17 oct 2018; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Problemas del boletín
2 Otros problemas
- 2.1 Equilibrio estático
- 2.2 Dinámica

1 Problemas del boletín

1.1 Ejemplos de sistemas de referencia inerciales

Estima para qué rango de aceleraciones un sistema de referencia solidario con los siguientes objetos es un buen sistema de referencia inercial (busca en Internet los datos numéricos que no conozcas):

Un laboratorio en la superficie de la Tierra.
Un sistema que viaje con la Tierra alrededor del Sol (sin rotar con ella)
Un sistema que viaje con el Sol alrededor del centro de la Vía Láctea.

1.2 Partícula con dos muelles verticales

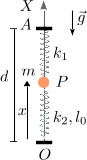
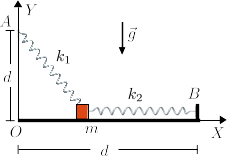
Una masa $m$ está conectada a dos muelles como se indica en la figura. El muelle superior tiene constante elástica $k 1$ y longitud natural nula, mientras que el inferior tiene constante elástica $k 2$ y longitud natural $l 0$ . Además la gravedad actúa en dirección vertical. Determina la posición de equilibrio de la masa.

1.3 Masa colgando de dos cuerdas

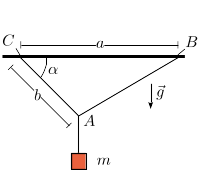
Una masa $m$ cuelga del conjunto de cuerdas ideales sin masas como se indica en la figura. Los datos del problema son las longitudes $a$ y $b$ y el ángulo $α$ . Si el sistema está en equilibrio, determina la tensión en las tres cuerdas.

1.4 Partícula en un rectángulo con muelle

En el sistema de la figura el muelle tiene longitud natural nula y constante de recuperación $k$ . La masa de la partícula es $m$ .

Si los vínculos son lisos ¿cuál de las posiciones de la partícula puede ser de equilibrio? ¿Y si los vínculos son rugosos?
Determina las posiciones de equilibrio en los casos en que éste pueda existir.
Supongamos ahora que hay rozamiento. Suponiendo que la posición de la partícula está fijada, calcula la fuerza de rozamiento que debe actuar para que haya equilibrio estático.
A partir del resultado del apartado anterior, encuentra el rango de posiciones de equilibrio en cada uno de los casos.

1.5 Fuerza unidireccional

Una partícula de masa $m$ está sometida a una fuerza constante 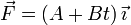$\vec{F}=(A + Bt)\,\vec{\imath}$ . Si parte del reposo y desde el origen del sistema de referencia, encuentra la posición y la velocidad de la partícula en cualquier instante.

1.6 Fuerza sobre tres masas yuxtapuestas

Tres masas $m 1$ , $m 2$ y $m 3$ se encuentran yuxtapuestas sobre una superficie horizontal sin rozamiento. Sobre la primera de ellas actúa una fuerza horizontal $F$ . Calcula

La aceleración de las masas.
La fuerza resultante sobre cada una de ellas.
Las magnitudes de las fuerzas de contacto entre ellas.

1.7 Masa sobre una cuña con la misma aceleración

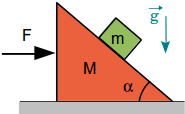
En el sistema de la figura, ambos bloques están en reposo cuando se aplica la fuerza $F$ , ¿Cuál debe ser la magnitud de la fuerza para que el bloque de masa $m$ permanezca estacionario respecto a la cuña? Todas las superficies son lisas.

1.8 Masa sobre una balanza de resorte en un ascensor

Una masa $M$ se encuentra sobre una balanza de resorte. Ambos objetos están dentro de un ascensor. ¿Qué fuerza mide la balanza cuando el ascensor tiene una aceleración $a 0$ vertical? La gravedad actúa en dirección vertical con sentido hacia abajo.

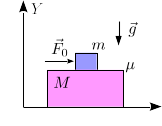
1.9 Masa sobre otra masa con rozamiento

Un bloque de masa $m$ puede deslizar sobre otro bloque de masa $M = 2 m$ . El contacto entre los dos bloques es rugoso con coeficiente de rozamiento estático $μ$ . El bloque de masa $M$ desliza sin rozamiento sobre una superficie horizontal. Se aplica sobre el bloque superior una fuerza horizontal 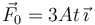$\vec{F}_0 = 3At\,\vec{\imath}$ , con $A > 0$ y constante y $t$ el tiempo.

Si la masa superior no desliza respecto de la inferior, ¿cuál es la aceleración de las masas?
¿En que instante la masa superior empieza a deslizar respecto a la inferior?
Supongamos ahora que hay rozamiento entre el bloque inferior y la superficie horizontal, con un coeficiente de rozamiento dinámico $μ$ . ¿Cuánto vale la aceleración de los bloques en este caso?
¿En que instante empieza a deslizar el bloque superior respecto del inferior en este caso?

1.10 Partícula ensartada en un aro circular

Se tiene un aro circular de radio $R$ . Engarzado en él hay una masa $m$ que puede deslizar siguiendo la circunferencia del aro bajo la acción de la gravedad.

Suponiendo que el contacto es liso, encuentra las ecuaciones que describen el movimiento de la masa en función del ángulo $α$ de la figura.
Soltamos la masa con velocidad inicial nula y un ángulo inicial 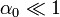$\alpha_0\ll1$ . Encuentra la función $α(t)$ que describe el movimiento de la masa.
Supongamos ahora que nos dicen que la masa realiza un movimiento circular uniforme con frecuencia angular $Ω$ . Encuentra la expresión de la fuerza de ligadura en función del ángulo $θ$ . ¿Es constante? En este caso, ¿el vínculo es liso o rugoso?

1.11 Partícula sometida a la acción de dos muelles

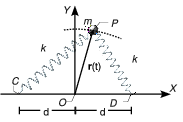
Una partícula $P$ , de masa $m$ , se mueve en el plano horizontal sometida a la acción de dos resortes elásticos ideales e idénticos, de constante $k$ y longitud natural nula. Los puntos de anclaje son $C ( - d,0)$ y $D (d,0)$ , respectivamente

Escribe la ecuación diferencial que determina el movimiento de la partícula.
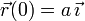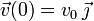Si las condiciones iniciales son $\vec{r}(0)=a\,\vec{\imath}$ y $\vec{v}(0)=v_0\,\vec{\jmath}$ , encuentra las expresiones que dan la posición y la velocidad de la partícula en todo instante de tiempo.
Determina, para todo instante de tiempo, el momento cinético, $\vec{L}_O$ , de la partícula $P$ respecto al origen de coordenadas $O$ , así como su energía mecánica, $E$ . ¿Qué teoremas de conservación explican las propiedades de estas magnitudes en este problema?

2 Otros problemas

2.1 Equilibrio estático

2.1.1 Equilibrio de una partícula bajo la acción de tres muelles

Una partícula libre de masa $m$ está unida a tres muelles de longitud natural nula y constantes elásticas $k A$ , $k B$ y $k C$ . Cada uno de los muelle tiene el otro extremo fijado en un punto. Las coordenadas de los puntos de fijación son $A ( - a,0,0)$ , $B (a,0,0)$ y $C (0, a,0)$ .

Calcula la posición de equilibrio de la partícula.
Considera las situaciones siguientes
1. $m = 0$ y $k A = k B = k C = k$
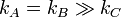
2. $m = 0$ y $k_A=k_B\gg k_C$
3. $k A = k B = k C = k$ y $m > > k a / g$ .

2.1.2 Equilibrio de una partícula sobre una esfera lisa

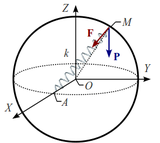
Un punto material $M$ de peso $P$ está obligado a permanecer en la superficie de una esfera de radio $R$ y centro $O$ . Además, $M$ es atraído por un punto fijo $A$ del ecuador de la superficie esférica, debido a la existencia de un resorte elástico ideal, de longitud natural nula y de constante recuperadora 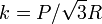$k=P/\sqrt{3}R$ , que conecta ambos puntos. Determina las posiciones de equilibrio del punto material $M$ , y la fuerza de reacción vincular en ellas.

2.1.3 Equilibrio de una partícula sobre una hélice

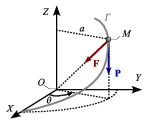
Un punto material $M$ , de peso $P$ , está vinculado a la hélice $Γ$ , definida en el sistema de referencia cartesiano $O X Y Z$ por la ecuación vectorial 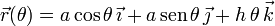$\vec{r}(\theta)=a\cos\theta\,\vec{\imath}+a\,\mathrm{sen}\,\theta\,\vec{\jmath}+h\,\theta\,\vec{k}$ . Determina la posición de equilibrio estático del punto $M$ si, además, este es atraído por el origen por una fuerza $\vec{F}$ proporcional a la distancia entre ambos puntos, siendo $k$ la constante de proporcionalidad.

2.1.4 Particula con un muelle horizontal y otro inclinado

Un partícula de masa $m$ reposa sobre un plano horizontal sin rozamiento. Está atada a dos muelles de constantes elásticas $k 1$ y $k 2$ y longitud natural nula, anclados en los puntos $A$ y $B$ . La partícula no puede desplazarse a lo largo del eje $O Z$ .

Dibuja el diagrama de cuerpo libre de la partícula.
Condición para que la masa no se separe del plano.
Posición de equilibrio de la partícula en la situación del apartado anterior.
Supongamos que existe rozamiento entre la partícula y el plano, con un coeficiente de rozamiento estático $μ e$ . Si $x m$ es la coordenada de la partícula sobre el eje $O X$ , en situación de equilibrio, calcula el módulo de la fuerza de rozamiento.

2.1.5 Partícula en semiaro con muelle anclado en un extremo

Una partícula de masa $m$ está engarzada en un semiaro de radio $R$ cuyo centro coincide con el origen de coordenadas, como se observa en la figura. La partícula está conectada a un muelle de constante elástica $k$ y longitud natural nula conectada al punto $A$ . La gravedad actúa hacia abajo.

Dibuja el diagrama de cuerpo libre de la partícula en situación de contacto rugoso, indicando de que fuerzas se conoce su dirección y sentido y de cuales no.
Escribe la expresión que da la fuerza que el muelle ejerce sobre la partícula.
En situación de contacto liso, encuentra el valor del ángulo de equilibrio.
Supongamos ahora que el contacto es rugoso con un coeficiente de rozamiento estático $μ$ . Además el ángulo $θ$ es tal que $cosθ = 3 / 5$ , y el sistema se ajusta de modo que $m g = k R$ . ¿Cuál es valor mínimo del coeficiente de rozamiento para que esta configuración sea de equilibrio?

2.2 Dinámica

2.2.1 Partícula sobre plano inclinado con muelle y cuerda

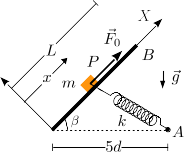
Una partícula de masa $m = 5 m 0$ puede moverse sobre un plano inclinado que forma un ángulo $β$ con la horizontal. Este ángulo es tal que $cosβ = 4 / 5$ y, por tanto, 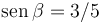$\mathrm{sen}\,\beta=3/5$ . La partícula está conectada a un muelle de constante elástica $k$ y longitud natural nula. El otro extremo del muelle se conecta al punto fijo $A$ indicado en la figura. 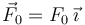La masa también está conectada a una cuerda inextensible sin masa sobre la que se ejerce una fuerza constante $\vec{F}_0=F_0\,\vec{\imath}$ . El sistema se ajusta de modo que $m 0 g = k d$ .

Dibuja el esquema de cuerpo libre de la partícula, teniendo en cuenta el rozamiento. Indica de que fuerzas se conoce su sentido a priori y de cuales no.
Escribe la expresión que da la fuerza del muelle.
Suponiendo que no hay rozamiento, ¿cuánto debe valer $F 0$ para que la posición de equilibrio venga dada por $x = 3 d$ ?
Con el valor de $F 0$ calculado en la pregunta anterior, ¿qué condición debe cumplir el coeficiente de rozamiento estático $μ$ , entre la masa y el plano, para que el punto $O$ sea de equilibrio?
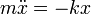Supongamos que no hay rozamiento. ¿Cuanto debe valer $F 0$ para que la ecuación de movimiento de la masa tenga la forma $m\ddot{x}=-kx$ ?

2.2.2 Partícula en el campo gravitatorio terrestre

Una partícula de masa $m$ se mueve en el seno del campo gravitatorio terrestre cerca de la superficie, de modo que la aceleración de la gravedad puede suponerse constante y dirigida verticalmente a la superficie (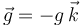 $\vec{g}=-g\,\vec{k}$ ). Analiza el movimiento de la partícula para las siguientes condiciones iniciales

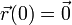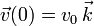$\vec{r}(0)=\vec{0}$ , $\vec{v}(0)=v_0\,\vec{k}$ .
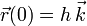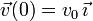$\vec{r}(0)=h\,\vec{k}$ , $\vec{v}(0)=v_0\,\vec{\imath}$ .
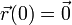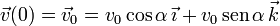$\vec{r}(0)=\vec{0}$ , $\vec{v}(0)=\vec{v}_0=v_0\cos\alpha\,\vec{\imath} + v_0\,\mathrm{sen}\,\alpha\,\vec{k}$ .

2.2.3 Muelle vertical

Se tiene un muelle vertical de constante $K$ y longitud natural $l 0$ . El sistema está sometido a la acción de la gravedad, 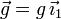$\vec{g}=g\,\vec{\imath}_1$ .

Se cuelga una masa $m$ del extremo del muelle. ¿Cuál es la nueva elongación del muelle cuando se alcanza el equilibrio?
Partiendo de la situación del apartado anterior, estiramos la masa de modo que la elongación del muelle aumenta una distancia $L$ , y lo soltamos. Describe las fuerzas actuando sobre la masa justo después de soltarla.
Aplicando la Segunda Ley de Newton calcula la posición de la masa como función del tiempo. ¿Que movimiento describe?

Nota : Podemos suponer que todos los desplazamientos del muelle son verticales.

2.2.4 Partícula sometida a la acción de dos muelles colineales

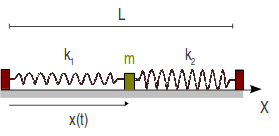
Se tiene el sistema de la figura, formado por dos muelles de longitud natural nula y constantes elásticas $k 1$ y $k 2$ . Los puntos de anclaje de los muelles están separados por una distancia $L$ . Una partícula de masa $m$ está conectada a los dos muelles y se mueve bajo la acción de éstos. El rozamiento con la superficie es despreciable. 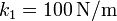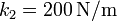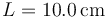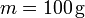Los valores numéricos de los parámetros del problema son $k_1=100\,\mathrm{N/m}$ , $k_2=200\,\mathrm{N/m}$ , $L = 10.0\,\mathrm{cm}$ , $m=100\,\mathrm{g}$ .

Calcula la posición de equilibrio de la partícula.
Calcula la energía potencial elástica de la partícula cuando está en su posición de equilibrio.
Estando la partícula en la posición de equilibrio, se le da un empujón hacia la derecha de modo que su velocidad inicial es $v 0$ . ¿Cuál es el período de las oscilaciones de la partícula?
Si el valor numérico de la velocidad inicial es 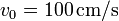$v_0=100\,\mathrm{cm/s}$ , ¿cuál es la amplitud de las oscilaciones de la partícula?

2.2.5 Partícula con dos muelles apoyada sobre un plano vertical

Un partícula de masa $m$ reposa sin rozamiento sobre un plano vertical definido por los puntos $A$ y $B$ de la figura. Está atada a dos muelles de constantes elásticas $k 1$ y $k 2$ y longitud natural nula, anclados en los puntos $O$ y $C$ , respectivamente. La partícula no puede deplazarse a lo largo del eje $O Z$ . El plano $A B$ puede desplazarse a lo largo del eje $O X$ de modo que se mantiene siempre vertical.

Dibuja el diagrama de cuerpo libre de la partícula.
¿Que condición debe cumplirse para que el punto de equilibrio de la masa esté sobre el eje $O X$
¿Qué condición debe cumplir $x P$ para que el plano $A B$ ejerza una fuerza sobre la partícula?
Supongamos que existe rozamiento entre la partícula y el plano, con un coeficiente de rozamiento estático $μ e$ . Si $y m$ es la coordenada de la partícula sobre el eje $O Y$ , calcula el módulo de la fuerza de rozamiento.
En la situación con rozamiento, supongamos que $k 1 = k 2 = k$ , $m g = 2 k d$ , $d = l$ y $x P = l / 4$ . ¿Cuál es el rango de posiciones de equilibrio de la partícula sobre el plano?

2.2.6 Partícula en hilo vertical con dos muelles

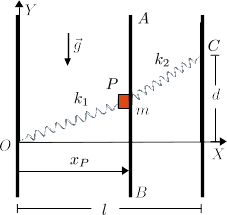
Una partícula de masa $m$ puede moverse a lo largo del eje vertical $Y$ . Está conectada a dos muelles como se indica en la figura. El muelle anclado en $A$ tiene constante elástica $k$ y longitud natural nula. El muelle anclado en $O$ tiene constante elástica $k$ y longitud natural $d$ . El contacto entre la masa y el eje $Y$ es rugoso con coeficiente de rozamiento estático $μ$ . La partícula puede moverse a lo largo de todo el eje $Y$ , por encima y por debajo del punto $O$ .

Dibuja el esquema de cuerpo libre de la partícula, teniendo en cuenta el rozamiento, indicando de que fuerzas se conoce su sentido a priori y de cuales no.
Escribe las expresiones que dan las fuerzas de los muelles.
Encuentra la posición de equilibrio sin rozamiento.
Volviendo a considerar el rozamiento, y asumiendo que $m g = k d / 2$ , encuentra el rango de posiciones de equilibrio.
Considera de nuevo que no hay rozamiento. Ahora no hay ninguna condición sobre $m g$ . ¿Cual es el período de las oscilaciones de la partícula?
Supongamos ahora que el sistema se ajusta de modo que 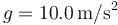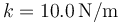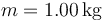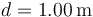$g=10.0\,\mathrm{m/s^2}$ , $k=10.0\,\mathrm{N/m}$ , $m=1.00\,\mathrm{kg}$ , $d=1.00\,\mathrm{m}$ . En el instante inicial la masa se suelta en reposo desde el punto 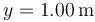$y=1.00\,\mathrm{m}$ . ¿Cuál es la posición de la partícula en cada instante?

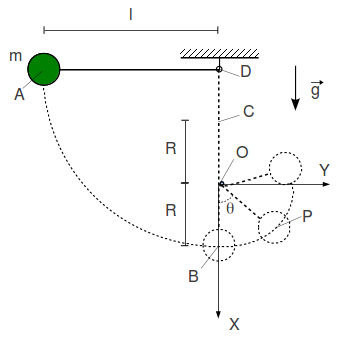
2.2.7 Péndulo enrollándose alrededor de una clavija delgada

Un péndulo consiste en una pequeña masa $m$ atada al extremo de una cuerda inextensible y sin masa de longitud $l$ . La masa se coloca en el plano horizontal y se suelta. En el punto más bajo de la oscilación (punto $B$ ), la cuerda choca con una clavija delgada (punto $O$ ) situada a una distancia $R$ por encima de del punto $B$ .

Para el punto más bajo de la oscilación (punto $B$ ) calcula el módulo de la velocidad de la masa, su cantidad de movimiento y su momento cinético respecto al punto $D$ .
Expresa en coordenadas polares la posición respecto del punto $O$ de la masa después de que la cuerda haya chocado con la clavija (punto $P$ ). Encuentra la expresión de la velocidad y la aceleración de la masa.
Para el movimiento de la masa después del punto $B$ , encuentra la expresión de la ecuación diferencial que rige la variación del ángulo $θ$ , la expresión que da la tensión de la cuerda y las condiciones iniciales de la ecuación diferencial en el punto $B$ .
¿Cuál es la condición que debe cumplir la distancia $R$ para que la masa describa al menos un círculo completo alrededor de la clavija, es decir, para que llegue al punto $C$ ?

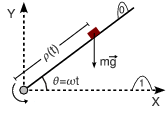
2.2.8 Bloque sobre plano inclinado girando

Una partícula puntual de masa $m$ se mueve sobre un plano inclinado. A su vez, el plano gira de modo que el ángulo con la horizontal es $θ(t) = ω t$ . Sobre la masa actúa además la gravedad 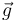$\vec{g}$ . El contacto entre la partícula y el plano es liso.

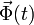Encuentra la expresión de la ecuación diferencial que cumple la distancia de la partícula al origen de coordenadas, $ρ(t)$ , así como la expresión que da el valor de la fuerza de reacción vincular $\vec{\Phi}(t)$ .
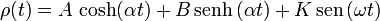
Demuestra que, para los valores apropiados de las constantes $α$ y $K$ , la expresión siguiente es solución de la ecuación diferencial. ¿Cuáles son esos valores de $α$ y $K$ ? $\rho(t) = A\,\cosh(\alpha t) + B\,\mathrm{senh}\,(\alpha t) + K\,\mathrm{sen}\,(\omega t)$
Si en el instante inicial tenemos $ρ(0) = 0$ y 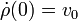$\dot{\rho}(0)=v_0$ encuentra cuánto valen las constantes $A$ y $B$ de la expresión anterior.
¿Se conserva la energía mecánica del sistema? Razona la respuesta.

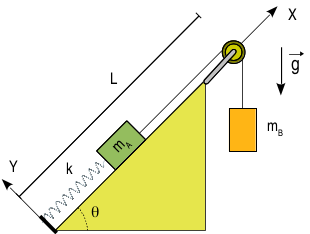
2.2.9 Masa sobre un plano inclinado conectado a un muelle y otra masa

En el sistema de la figura, la masa $m A$ desliza sin rozamiento sobre el plano inclinado. El muelle tiene constante elástica $k$ y longitud natural nula. La longitud de la cuerda es $l = L$ . La cuerda se supone que tiene masa nula y que siempre se mantiene tensa. La masa $m B$ se mueve de modo que la cuerda se mantiene siempre vertical. La cuña se supone estática en todo el problema.

Dibuja el diagrama de cuerpo libre de las dos masas.
Determina la posición $x e q$ de la masa $m A$ cuando el sistema está en equilibrio.
La masa $m A$ se separa de su posición de equilibrio y se suelta. Escribe la ecuación de movimiento de la masa $m A$ . Demuestra que realiza un movimiento armónico simple y encuentra su período.
Suponiendo que el origen de energía potencial se sitúa en la base de la cuña, ¿cuánto vale la energía mecánica del sistema cuando $x A = L / 2$ , estando las dos masas en reposo?

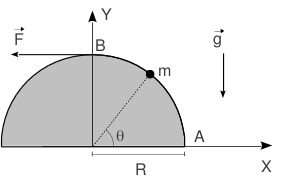
2.2.10 Partícula sobre una circunferencia tirada por una cuerda

Una partícula de masa $m$ se mueve a lo largo de una circunferencia de radio $R$ sin rozamiento. Una fuerza horizontal tira de ella por medio de una cuerda que se mantiene siempre pegada a la circunferencia. La partícula está sometida a la acción de la gravedad. }

Expresa los vectores de posición, velocidad y aceleración de la partícula en coordenadas polares.
Dibuja el diagrama de cuerpo libre de la partícula y expresa las fuerzas que actúan sobre ella en coordenadas polares.
Escribe las ecuaciones de movimiento de la partícula. ¿Cuál es la condición que debe cumplir la fuerza $\vec{F}$ para que la celeridad de la partícula sea constante durante el movimiento? ¿Cuanto vale la fuerza de reacción vincular en este caso?
Supongamos que la partícula parte del reposo desde el punto $A$ . Al llegar al punto $B$ su velocidad es de 12.0 m/s. Calcula el trabajo realizado por la fuerza $F$ en el movimiento desde $A$ hasta $B$ .

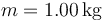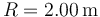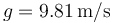Datos numéricos: $m=1.00\,\mathrm{kg}$ , $R=2.00\,\mathrm{m}$ , $g=9.81\,\mathrm{m/s}$ .

2.2.11 Masa conectada a dos muelles

La masa $m$ de la figura puede deslizarse sin rozamiento sobre una superficie horizontal. Conectados a ella hay dos resortes de longitud natural nula y constantes elásticas $k 1$ y $k 2$ . Los muelles están anclados en los puntos $A$ y $B$ respectivamente.

Dibuja el diagrama de cuerpo libre de la masa.
Encuentra la posición de equilibrio mecánico de la masa.
Situamos la masa en su posición de equilibrio. Le damos un empujón hacia la derecha de modo que en $t = 0$ el módulo de su velocidad es $v 0$ . Encuentra la ecuación diferencial que describe el movimiento de la partícula.
Encuentra la función que da la posición $x (t)$ de la masa.
En el caso $k 1 = k 2$ , ¿cuál es el valor máximo de la velocidad para que la partícula no choque con la pared de la derecha?

2.2.12 Dos partículas conectadas por un muelle

Dos partículas con la misma masa $m$ están unidas por un muelle de constante elástica $k$ y longitud natural $l 0 = 2 d$ . Debido a una perturbación externa, las dos masas empiezan a oscilar. Después de la perturbación, cada masa está sometida únicamente a la acción del muelle. Los ejes $X$ e $Y$ están indicados en la figura. El origen de coordenadas está en el punto medio entre las dos masas. Suponemos que el movimiento es rectilíneo sobre el eje $X$ .

Fuerza sobre las partículas
Encuentra la frecuencia natural de las oscilaciones
Esta configuración puede modelar una molécula de hidrógeno (H2) o de Deuterio (D2), usando la misma constante elástica y la misma longitud natural para las dos. La frecuencia vibracional de la molécula de hidrógeno es 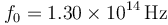$f_0=1.30\times10^{14}\,\mathrm{Hz}$ . Sabiendo que la masa de la molécula de deuterio es el doble de la masa de la molécula de hidrógeno, ¿cuál es la frecuencia de vibración de la molécula de deuterio, aproximadamente?

2.2.13 Partícula en barra giratoria con dos muelles

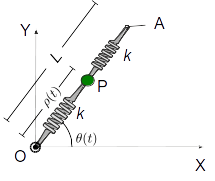
Una partícula $P$ de masa $m$ desliza sin rozamiento a lo largo de una varilla $O A$ de longitud $L$ . Actúan sobre ella dos muelles, ambos de longitud natural nula y constante elástica $k$ , anclados en los puntos $O$ y $A$ , respectivamente. El efecto de la gravedad es despreciable.

Escribe las expresiones del vector posición y velocidad de la partícula en coordenadas cartesianas y polares. Deja las expresiones en función de $r (t)$ , $θ(t)$ y sus derivadas temporales.
Dibuja el diagrama de cuerpo libre de la partícula y escribe, usando coordenadas polares, las dos componentes de la Segunda Ley de Newton aplicada al movimiento de la partícula.
Supongamos que la barra gira con velocidad angular constante $ω$ . Durante el giro, la distancia de la partícula al origen permanece constante. ¿Cuánto vale esa distancia? ¿Que condición debe cumplirse para que esta situación sea posible físicamente?
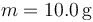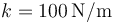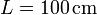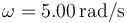Calcula el valor numérico de los módulos de todas las fuerzas que actúan sobre la partícula en la situación del apartado anterior y con estos valores numéricos: $m=10.0\,\mathrm{g}$ , $k=100\,\mathrm{N/m}$ , $L=100\,\mathrm{cm}$ , $\omega=5.00\,\mathrm{rad/s}$ .

2.2.14 Masa en barra rotando con muelle

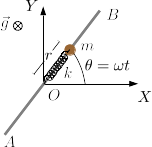
Una partícula de masa $m$ puede moverse a lo largo de una barra de longitud $L$ . La partícula está conectada al extremo de un muelle de constante elástica $k$ y longitud natural $l 0$ . El ángulo que forma la barra con el eje horizontal $O X$ es $θ = ω t$ , donde $ω$ es una constante conocida. La barra se situá en un plano horizontal, de modo que la gravedad actúa como se indica en la figura. El contacto entre la masa y la barra es liso.

Encuentra la expresión de los vectores de posición, velocidad y aceleración de la masa usando las coordenadas y la base polares.
Encuentra las expresiones del momento cinético de la masa respecto a $O$ y su energía mecánica.
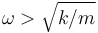Determina el valor de $r$ para el que la masa no se mueve respecto a la barra. ¿Cuanto vale la fuerza de reacción vincular en este caso? ¿Que ocurre si $\omega>\sqrt{k/m}$ ?.
Encuentra la ecuación diferencial de movimiento para $r (t)$ . ¿Que condición debe cumplirse para que el movimiento sea armónico simple?

2.2.15 Masa en barra fija con muelle

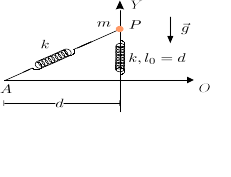
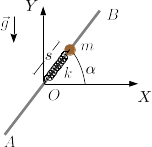
Una partícula de masa $m$ puede moverse a lo largo de una barra de longitud $L$ . La partícula está conectada al extremo de un muelle de constante elástica $k$ y longitud natural nula. El ángulo que forma la barra con el eje horizontal $O X$ es $α$ , y no cambia con el tiempo. La gravedad actúa como se indica en la figura. El coeficiente de rozamiento estático entre la partícula y la barra es $μ$ .

Dibuja el diagrama de cuerpo libre de la partícula, así como la expresión de las fuerzas que actúan sobre ella.
Suponiendo que no hay rozamiento, determina el valor de equilibrio de $s$ ( $s = 0$ corresponde al punto $O$ de la barra).
Si ahora incluimos el rozamiento, calcula el rango posible de valores de equilibrio de $s$ .
Supongamos de nuevo que no hay rozamiento. Encuentra la expresión del vector velocidad y aceleración de la partícula.
Aplicando la Segunda Ley de Newton, encuentra la ecuación de movimiento, así como la frecuencia de las oscilaciones.

2.2.16 Péndulo cónico

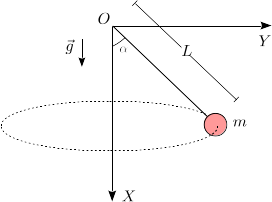
Una masa $m$ cuelga de un hilo tenso, inextensible y sin masa, de longitud $L$ . La masa se mueve de modo que describe un movimiento circular uniforme en torno al eje $X$ , como se indica en la figura. La masa está también sometida a la acción de la gravedad. En el instante mostrado en la figura la partícula está en el plano $O X Y$ .

Dibuja el diagrama de cuerpo libre de la masa. Añade a este diagrama el vector aceleración de la partícula. ¿Cuanto vale el radio de la circunferencia que describe la partícula?
Aplicando la Segunda Ley de Newton, determina la relación entre la rapidez de la partícula y el ángulo $α$ que forma el hilo con la vertical.
Suponiendo que $α = π / 4$ , y que la dirección de la velocidad apunta en el sentido negativo del eje $Z$ , calcula el momento angular de la partícula respecto al punto $O$ en el instante que se muestra en la figura, así como su derivada temporal.

2.2.17 Masa deslizando verticalmente sobre otra masa con un muelle

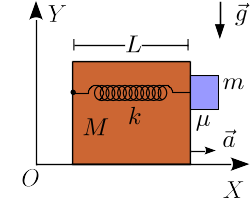
El bloque de masa $M$ y longitud $L$ de la figura se mueve hacia la derecha, con una aceleración constante 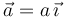$\vec{a} = a\,\vec{\imath}$ . Un bloque pequeño de masa $m$ puede deslizar sobre la cara lateral del bloque grande. Un muelle horizontal, con constante elástica $k$ y longitud natural nula, está anclado en el lado izquierdo del bloque grande. El muelle se mantiene siempre horizontal. El contacto entre los dos bloques es rugoso, con un coeficiente de rozamiento estático $μ = 0.5$ . ¿Para que valores de $a$ el bloque pequeño no desliza sobre el grande?

2.2.18 Dos bloques superpuestos conectados a un muelle

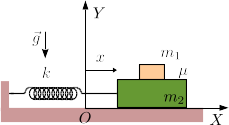
Un bloque de masa $m 2$ desliza sin rozamiento sobre una superficie horizontal. El bloque está conectado a un muelle de constante elástica $k$ . El muelle se encuentra relajado cuando la coordenada $x$ de la figura es cero. Encima de este bloque se pone otro de masa $m 1$ . El contacto entre los dos bloques es rugoso, caracterizado por un coeficiente de rozamiento estático $μ$ . Los bloques están sometidos a la acción de la gravedad.

Dibuja el diagrama de fuerzas de cada bloque. Exprésalas en el sistema de ejes de la figura.
Suponiendo que los dos bloques se mueven a la vez, encuentra la ecuación diferencial para $x (t)$ , así como los valores de todas las fuerzas. (Pueden quedar en función de $x (t)$ )
Si las condiciones iniciales son $x (0) = 0$ y 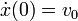$\dot{x}(0)=v_0$ , con $v 0$ una constante positiva, encuentra la posición y velocidad de los bloques en función del tiempo.
¿Cuál es el valor máximo de $v 0$ para que el bloque de arriba no deslice respecto al de abajo?

Problemas de Dinámica del punto (GIC)