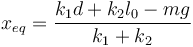Partícula con dos muelles verticales (GIC)
De Laplace
1 Enunciado
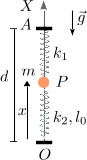
Una masa m está conectada a dos muelles como se indica en la figura. El muelle superior tiene constante elástica k1 y longitud natural nula, mientras que el inferior tiene constante elástica k2 y longitud natural l0. Además la gravedad actúa en dirección vertical. Determina la posición de equilibrio de la masa.
2 Solución
La partícula puede moverse sólo en posición vertical. La figura de la derecha muestra las fuerzas que actúan sobre la partícula, a saber, su peso y las fuerzas de los muelles. Todas ellas son fuerzas activas, en este caso no hay ninguna fuerza vincular. Las expresiones de las fuerzas son, utilizando el eje OX de la figura,
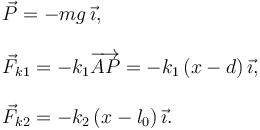
El muelle 1 tiene longitud natural nula, mientras que el segundo tiene longitud natural l0. Por eso las expresiones de las fuerzas son diferentes. Señalemos también que antes de resolver el problema conocemos el sentido de dos fuerzas: el peso, hacia abajo, y la del muelle 1, hacia arriba, por tener longitud natural nula. El sentido de la fuerza ejercida por el muelle 2 depende de la posición de la partícula.
Tenemos una incógnita en el sistema, el valor de x en el equilibrio. La condición de equilibrio es
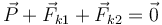
Como las fuerzas tienen todas la misma dirección esta ecuación vectorial implica una ecuación escalar
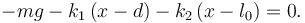
Despejando obtenemos la posición de equilibrio