Masa sobre un plano inclinado conectado a un muelle y otra masa, Febrero 2013 (G.I.C.)

De Laplace

1 Enunciado

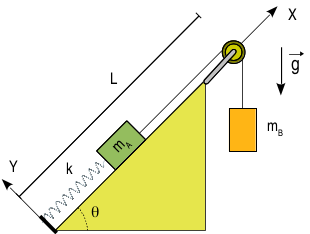
En el sistema de la figura, la masa m_A desliza sin rozamiento sobre el plano inclinado. El muelle tiene constante elástica k y longitud natural nula. La longitud de la cuerda es l = L. La cuerda se supone que tiene masa nula y que siempre se mantiene tensa. La masa m_B se mueve de modo que la cuerda se mantiene siempre vertical. La cuña se supone estática en todo el problema.

1. Dibuja el diagrama de cuerpo libre de las dos masas.
2. Determina la posición x_eq de la masa m_A cuando el sistema está en equilibrio.
3. La masa m_A se separa de su posición de equilibrio y se suelta. Escribe la ecuación de movimiento de la masa m_A. Demuestra que realiza un movimiento armónico simple y encuentra su período.
4. Suponiendo que el origen de energía potencial se sitúa en la base de la cuña, ¿cuánto vale la energía mecánica del sistema cuando x_A = L / 2, estando las dos masas en reposo?

2 Solución

2.1 Diagramas de cuerpo libre

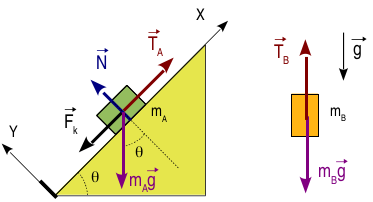
En el dibujo de la derecha se muestran las fuerzas que actúan sobre cada masa. Sobre la masa m_A actúan el peso, la fuerza del muelle, la tensión de la cuerda y la fuerza de reacción vincular del plano. El enunciado dice que no ha rozamiento con el plano inclinado.

Sobre la masa m_B sólo actúan el peso y la tensión de la cuerda.

2.2 Posición de equilibrio de la masa m_A

Para que la masa m_A esté en equilibrio la suma de fuerzas sobre ella debe ser cero. Es importante recordar que sólo hay que tener en cuenta las fuerzas que actúan directamente sobre la masa.

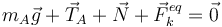
Podemos ignorar las componentes perpendiculares al plano del dibujo, por lo que la ecuación vectorial anterior nos da dos ecuaciones escalares, una de la componente X y otra de la componente Y. Utilizamos los ejes de la figura para expresar las fuerzas cuando la masa m_A está en su posición de equilibrio x_A.

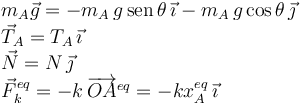
Considerando cada una de las componentes de la ecuación vectorial de equilibrio tenemos

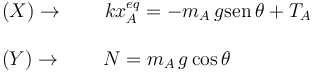
Tenemos 3 incógnitas: 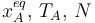. Necesitamos otra ecuación. La obtenemos aplicando la condición de equilibrio a la masa m_B.

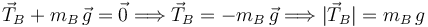
La polea no tiene masa (no nos dan ningún dato sobre ella) por lo que la tensión de la cuerda es la misma a los dos lados. Es decir

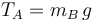
Entonces, la posición de equilibrio de la masa m_A es

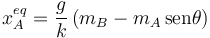
2.3 Movimiento de la masa m_A

Al separar la masa de la posición de equilibrio y soltarla, la suma de fuerzas sobre ella ya no es cero, con lo que adquiere una aceleración. Las fuerzas sobre ella tienen la misma expresión que antes, excepto la que ejerce el muelle. Para una posición arbitraria de la masa esta fuerza es

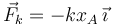
La ecuación de movimiento es la Segunda Ley de Newton

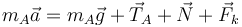
La aceleración sólo tiene componente paralela al eje X. Tenemos

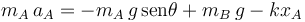
Dividimos por m_A y reordenamos los términos del lado derecho. Además, usamos que .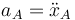

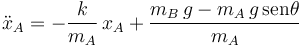
El primer término del lado derecho nos daría un movimiento armónico simple. Pero el segundo término molesta. Para quitarlo de en medio, describimos la posición de la masa no respecto al punto O, sino respecto a su posición de equilibrio. Esto es, definimos s(t) de modo que

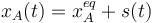
Derivando obtenemos

Al introducir este cambio en la ecuación diferencial, y utilizando el valor de 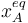obtenido en el apartado anterior llegamos a

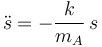
Esto corresponde a un movimiento armónico simple con frecuencia angular y período

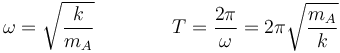
La masa oscila alrededor de su posición de equilibrio.

2.4 Energía mecánica del sistema

Cuando las masas están en reposo la energía mecánica tiene tres componentes: las energías potenciales gravitatorias de las dos masas y la energía elástica del muelle. Observando el dibujo de la derecha estas energías son

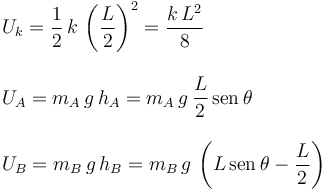
Hemos usado que la longitud de la cuerda es L. La energía mecánica total es