De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Estima para qué rango de aceleraciones un sistema de referencia solidario con los siguientes objetos es un buen sistema de referencia inercial (busca en Internet los datos numéricos que no conozcas):

Un laboratorio en la superficie de la Tierra.
Un sistema que viaje con la Tierra alrededor del Sol (sin rotar con ella)
Un sistema que viaje con el Sol alrededor del centro de la Vía Láctea.

2 Solución

2.1 Laboratorio en la superficie de la Tierra

Un sistema de referencia en reposo respecto a la superficie de la Tierra no es un sistema de referencia inercial (SRI) porque la Tierra rota. Cada punto de su superficie realiza un movimiento circular uniforme. Como vimos en un problema anterior, la aceleración centrípeta de este movimiento es

$a N = ω 2 R T cosλ.$

Aquí, $ω$ es la velocidad angular de rotación de la Tierra, $R T$ es su radio y $λ$ es la latitud del punto. Los datos numéricos son

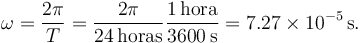
$\omega = \dfrac{2\pi}{T} = \dfrac{2\pi}{24\,\mathrm{horas}} \dfrac{1\,\mathrm{hora}}{3600\,\mathrm{s}} = 7.27\times 10^{-5}\,\mathrm{s}.$

Por otro lado 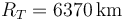$R_T=6370\,\mathrm{km}$ . Para un punto en el Ecuador $(λ = 0)$ su aceleración centrípeta es

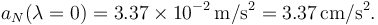
$a_N(\lambda=0) = 3.37\times 10^{-2}\,\mathrm{m/s^2} = 3.37\,\mathrm{cm/s^2}.$

Si la aceleración del movimiento que queremos estudiar es grande comparada con este valor podemos suponer que este sistema de referencia es inercial.

2.2 Sistema fijo respecto al centro de la Tierra

Si el sistema anterior no nos vale podemos escoger un sistema de referencia que se mueva con la Tierra alrededor del sol pero que no rote con ella. Este sistema tampoco es inercial, pues realiza un movimiento alrededor del Sol. Suponiendo que este movimiento es circular la aceleración centrípeta correspondiente es

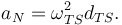
$a_N = \omega_{TS}^2 d_{TS}.$

La velocidad angular es

$\omega_{TS} = \dfrac{2\pi}{T} = \dfrac{2\pi}{1\,\mathrm{a\tilde{n}o}} \dfrac{1\,\mathrm{a\tilde{n}o}}{365\,\mathrm{d\acute{i}as}} \dfrac{1\,\mathrm{d\acute{i}a}}{24\,\mathrm{horas}} \dfrac{1\,\mathrm{hora}}{3600\,\mathrm{s}} = 1.99\times 10^{-7}\,\mathrm{s}.$

La distancia entre la Tierra y el Sol es $d_{TS} = 150\times10^{6}\,\mathrm{km}$ . Entonces

$a_N = 5.94\,\mathrm{m/s^2} = 5.94\,\mathrm{mm/s^2}.$

2.3 Sistema fijo respecto al Sol

Podemos mejorar el sistema de referencia si nos vamos al Sol y consideramos uno que esté fijo a él. La aceleración de este sistema se debe principalmente a la rotación del Sol alrededor del centro de la galaxia. El período de esta rotación es el año galáctico. Su valor está entre 225 y 250 millones de años. La distancia del Sol al centro de la Galaxia es aproximadamente 7900 pársec. La expresión de la aceleración centrípeta es similar a las de los apartados anteriores

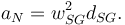
$a_N = w_{SG}^2d_{SG}.$

Los valores numéricos son

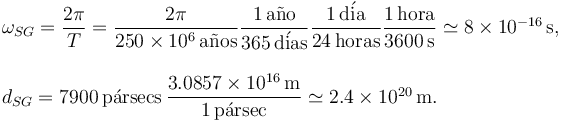
$\begin{array}{l} \omega_{SG} = \dfrac{2\pi}{T} = \dfrac{2\pi}{250\times 10^6\,\mathrm{a\tilde{n}os}} \dfrac{1\,\mathrm{a\tilde{n}o}}{365\,\mathrm{d\acute{i}as}} \dfrac{1\,\mathrm{d\acute{i}a}}{24\,\mathrm{horas}} \dfrac{1\,\mathrm{hora}}{3600\,\mathrm{s}} \simeq 8\times 10^{-16}\,\mathrm{s},\\ \\ d_{SG} = 7900\,\mathrm{p\acute{a}rsecs}\, \dfrac{3.0857\times 10^{16}\,\mathrm{m}}{1\,\mathrm{p\acute{a}rsec}} \simeq 2.4\times10^{20}\,\mathrm{m}. \end{array}$

Entonces la aceleración vale, aproximadamente

$a_N\simeq 1.5\times10^{-10}\,\mathrm{m/s^2}.$

Este sistema es una magnífica aproximación a un SRI.

Ejemplos de sistemas de referencia inerciales (GIC)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Laboratorio en la superficie de la Tierra

2.2 Sistema fijo respecto al centro de la Tierra

2.3 Sistema fijo respecto al Sol

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES