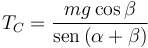De Laplace

1 Enunciado

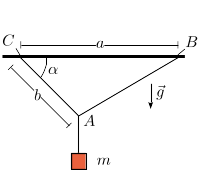
Una masa m cuelga del conjunto de cuerdas ideales sin masas como se indica en la figura. Los datos del problema son las longitudes a y b y el ángulo α. Si el sistema está en equilibrio, determina la tensión en las tres cuerdas.

2 Solución

2.1 Diagrama de fuerzas

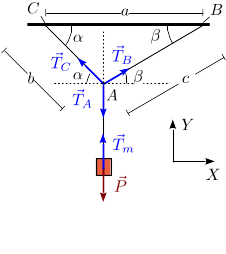
La figura de la derecha muestra las fuerzas que actúan sobre la masa y sobre el punto A. Escogemos las direcciones de los ejes X e Y como se indica en la figura. Las fuerzas sobre la masa son

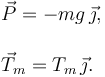
Las fuerzas sobre el punto A son

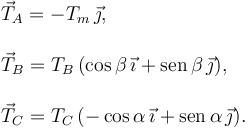
Para escribir 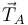hemos usado que en una cuerda sin masa la tensión es la misma en todos los puntos de la cuerda. Por tanto .

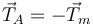Hay 3 incógnitas en las expresiones de las fuerzas: {T_m,T_B,T_C}. El ángulo β no es una incógnita, pues puede calcularse a partir del ángulo α y las longitudes de los lados a y b, como vemos a continuación.

2.2 Resolución del triángulo

Utilizando el teorema del seno obtenemos el ángulo β

Y usando el teorema del coseno obtenemos c

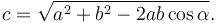
Entonces el ángulo β vale

En lo que sigue usaremos β, sabiendo que si queremos calcular su valor hemos de usar esta expresión

2.3 Eqquilibrio

Para que la masa esté en equilibrio debe cumplirse

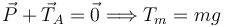
Hemos sustituido las expresiones de las fuerzas para obtener este valor.

Para obtener la condición de equilibrio de las fuerzas en A imaginamos que situamos en ese punto una masa muy pequeña m_a. La condición de equilibrio sería

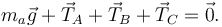
Ahora hacemos el límite . Entonces la condición de equilibrio queda

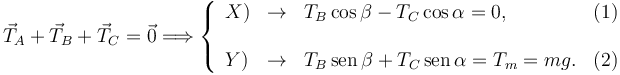
Para resolver este sistema, donde las incógnitas son T_B y T_C operamos como sigue. Multiplicamos la ecuación (1) por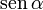 y la ecuación (2) por cosα y las sumamos

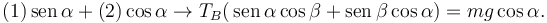
Entonces

Sustituyendo en (1) tenemos