Partícula sobre una circunferencia tirada por una cuerda, Julio 2013 (G.I.C.)

De Laplace

1 Enunciado

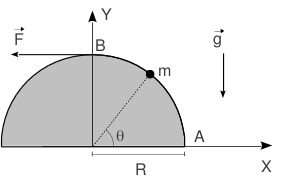
Una partícula de masa m se mueve a lo largo de una circunferencia de radio R sin rozamiento. Una fuerza horizontal tira de ella por medio de una cuerda que se mantiene siempre pegada a la circunferencia. La partícula está sometida a la acción de la gravedad. }

1. Expresa los vectores de posición, velocidad y aceleración de la partícula en coordenadas polares.
2. Dibuja el diagrama de cuerpo libre de la partícula y expresa las fuerzas que actúan sobre ella en coordenadas polares.
3. Escribe las ecuaciones de movimiento de la partícula. ¿Cuál es la condición que debe cumplir la fuerza para que la celeridad de la partícula sea constante durante el movimiento? ¿Cuanto vale la fuerza de reacción vincular en este caso?
4. Supongamos que la partícula parte del reposo desde el punto A. Al llegar al punto B su velocidad es de 12.0 m/s. Calcula el trabajo realizado por la fuerza F en el movimiento desde A hasta B.

Datos numéricos: , , .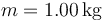

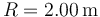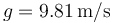2 Solución

2.1 Vectores posición, velocidad y aceleración en coordenadas polares

Escogemos el origen de coordenadas de la figura. La distancia de la partícula al origen es constante e igual a R, el radio de la circunferencia. Utilizando esto, los vectores pedidos son

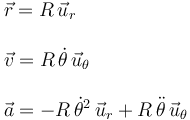
2.2 Fuerzas que actúan sobre la partícula

Las fuerzas sobre la partícula son el peso, , la reacción vincular de la circunferencia, y la ejercida por la cuerda, . Esta última es tangente a la circunferencia, y su módulo es igual a la de la fuerza de la figura del enunciado, . Utilizando coordenadas polares estas fuerzas son

2.3 Ecuaciones de movimiento

Aplicando la Segunda Ley de Newton obtenemos las ecuaciones de movimiento

Obtenemos una ecuación escalar para cada componente

La segunda ecuación es una ecuación diferencial de la que obtendríamos θ(t) (con las condiciones iniciales apropiadas). La primera ecuación nos daría el valor de la fuerza de reacción vincular Φ(t).

2.3.1 Condición para que la celeridad sea constante

La celeridad es el módulo de la velocidad. En este movimiento el módulo de la velocidad es

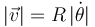
Si debe ser constante, entonces debe ser constante, esto es, 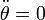. Otra forma de decir lo mismo es que la aceleración tangencial debe ser nula. De la ecuación para la componente acimutal obtenemos la condición que buscamos

2.4 Trabajo realizado por la fuerza en un movimiento concreto

En el movimiento descrito en el último apartado la partícula parte del reposo desde el punto Ay llega al punto B con velocidad . Durante el movimiento hay tres fuerzas que actúan sobre la partícula, pero sólo dos realizan trabajo, la gravedad y la de la cuerda. La gravedad es una fuerza conservativa, pero la ejercida por la cuerda no lo es. Por tanto la energía mecánica no se conserva. Pero podemos calcular su variación. Su valor es, tomado como origen de energía potencial gravitatoria la altura del punto A

La variación de energía mecánica es igual al trabajo realizado por las fuerzas no conservativas. Como en este caso sólo hay una, el trabajo realizado por la cuerda es